From the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the horizontal distance between AB and CD
To solve the problem, we will use the concept of angles of depression and trigonometry. Let's break it down step by step.
Step 1: Understand the Problem
We have a building AB that is 60 m high. From the top of the building, we observe the angles of depression to the top and bottom of a vertical lamp post CD. The angles of depression are 30∘ (to the top of the lamp post) and 60∘ (to the bottom of the lamp post).
Step 2: Draw a Diagram
Draw a vertical line representing the building AB with height 60 m. Next, draw a vertical line for the lamp post CD. Mark the points:
- A: the top of the building
- B: the bottom of the building
- C: the top of the lamp post
- D: the bottom of the lamp post
Step 3: Identify the Angles and Distances
From point A:
- The angle of depression to point C (top of the lamp post) is 30∘.
- The angle of depression to point D (bottom of the lamp post) is 60∘.
Let x be the horizontal distance from the base of the building B to the base of the lamp post D.
Step 4: Use Trigonometric Ratios
1. For the angle of depression to the top of the lamp post C:
- In triangle ACB:
tan(30∘)=ABBC=60x
- We know that tan(30∘)=1√3.
1√3=60x
- Cross-multiplying gives:
x=60√3
2. For the angle of depression to the bottom of the lamp post D:
- In triangle ADB:
tan(60∘)=ABBD=60x
- We know that tan(60∘)=√3.
√3=60x
- Cross-multiplying gives:
x=60√3=20√3
Step 5: Calculate the Height of the Lamp Post
Now, we need to find the height of the lamp post CD:
- The height of the lamp post h can be found using the height of the building and the height from the angle of depression to the bottom:
- Height from A to D:
h=AB−AD=60−20√3
Step 6: Conclusion
The horizontal distance x between the building AB and the lamp post CD is 20√3 meters.
Final Answer
The horizontal distance between the building and the lamp post is 20√3 meters.
---
We have a building AB that is 60 m high. From the top of the building, we observe the angles of depression to the top and bottom of a vertical lamp post CD. The angles of depression are 30∘ (to the top of the lamp post) and 60∘ (to the bottom of the lamp post).
Draw a vertical line representing the building AB with height 60 m. Next, draw a vertical line for the lamp post CD. Mark the points:
- A: the top of the building
- B: the bottom of the building
- C: the top of the lamp post
- D: the bottom of the lamp post
From point A:
- The angle of depression to point C (top of the lamp post) is 30∘.
- The angle of depression to point D (bottom of the lamp post) is 60∘.
1. For the angle of depression to the top of the lamp post C:
- In triangle ACB:
tan(30∘)=ABBC=60x
- We know that tan(30∘)=1√3.
1√3=60x
- Cross-multiplying gives:
x=60√3
- In triangle ADB:
tan(60∘)=ABBD=60x
- We know that tan(60∘)=√3.
√3=60x
- Cross-multiplying gives:
x=60√3=20√3
Now, we need to find the height of the lamp post CD:
- The height of the lamp post h can be found using the height of the building and the height from the angle of depression to the bottom:
- Height from A to D:
h=AB−AD=60−20√3
The horizontal distance x between the building AB and the lamp post CD is 20√3 meters.
The horizontal distance between the building and the lamp post is 20√3 meters.
Topper's Solved these Questions
Similar Questions
In the given figure, A from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
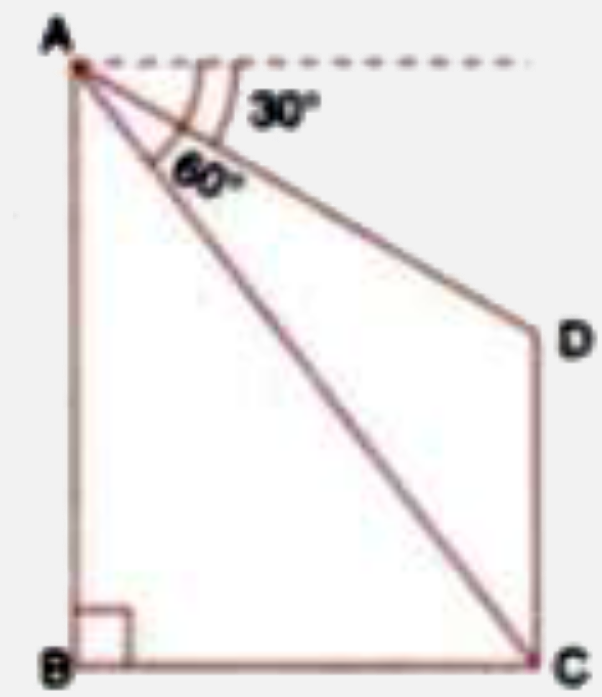
the horizontal distance between AB and CD
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the height of the lamp post.
View SolutionIn the igure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(i) the horizontal distance between AB and CD.
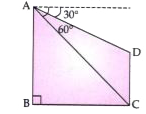
View SolutionFrom the top of a building AB , 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30o and 60o respectively. Find the difference between the heights of the building and the lamp post.
View SolutionIn the figure given, from the top of a building AB = 60 m high, the angles of depression of the top and bottom of a vertical lamp post CD are observed to be 30∘and60∘ respectively. Find :
(ii) the height of the lamp post.
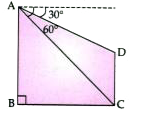
View SolutionFrom the top of a 50 m high tower, the angles of depression of the top and bottom of a pole are observed to be 45o and 60o respectively. Find the height of the pole.
View SolutionFrom the top of a building 60m high the angles of depression of the top and the bottom of a tower are observed to be 30o and 60o . Find the height of the tower.
View SolutionFrom te top of a tower , 60 meters high, the angles of depression of the top and bottom of a pole are αandβ respectively .Find the height of the pole.
View SolutionFrom the top of a cliff, the angle of depression of the top and bottom of a tower are observed to be 45∘ and 60∘ respectively. If the height of the tower is 20 m.
Find :
(i) the height of the cliff
(ii) the distance between the cliff and the tower.
View SolutionThe angles of depression of the top and bottom of 8m tall building from the top of a multistoried building are 30o and 45o respectively. Find the height of the multistoried building and the distance between the two buildings.
View Solution
