Question

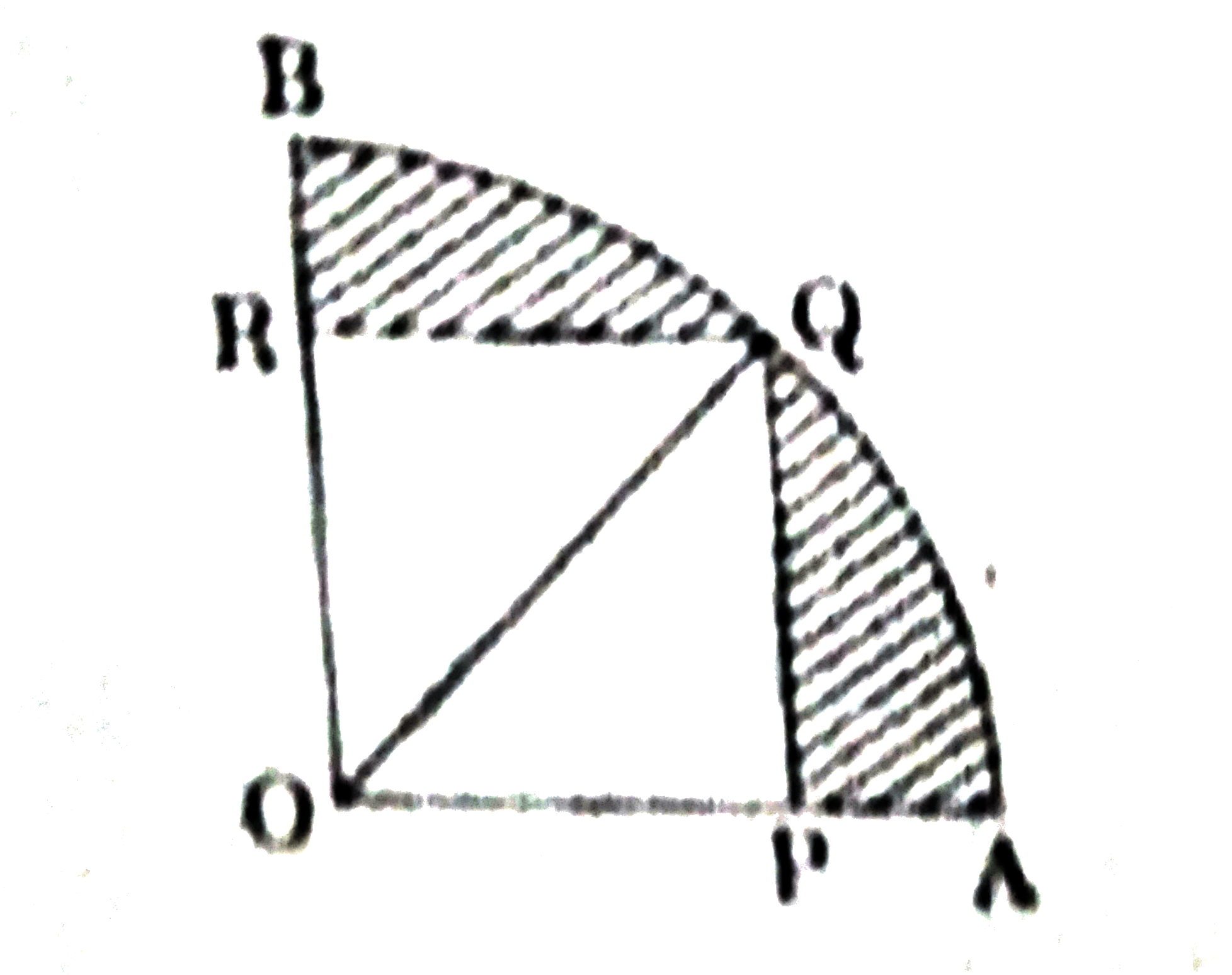
In Figure, $OACB$
is a
quadrant of a circle with centre $O$
and
radius 3.5 cm. If $OD=2cm$
, find the area of the (i) quadrant $OACB$
(ii)
shaded region.

Explanation

To solve the problem step by step, we will find the area of the quadrant $$OACB$$ and the area of the shaded region.

Step 1: Find the area of the quadrant \( OACB \)

The area of a quadrant of a circle can be calculated using the formula:
\( \text{Area of Quadrant} = \frac{1}{4} \times \pi r^2 \)
where \( r \) is the radius of the circle.

Given:
- Radius \( r = 3.5 \, \text{cm} \)

Substituting the value of \( r \):
\( \text{Area of Quadrant} = \frac{1}{4} \times \pi \times (3.5)^2 \)

Calculating \( (3.5)^2 \):
\( (3.5)^2 = 12.25 \)

Now substituting this back:
\( \text{Area of Quadrant} = \frac{1}{4} \times \pi \times 12.25 \)

Using \( \pi \approx \frac{22}{7} \):
\( \text{Area of Quadrant} = \frac{1}{4} \times \frac{22}{7} \times 12.25 \)

Calculating:
\( \text{Area of Quadrant} = \frac{22 \times 12.25}{4 \times 7} = \frac{271.5}{28} \approx 9.625 \, \text{cm}^2 \)

Step 2: Find the area of the shaded region

The shaded region is the area of the quadrant minus the area of triangle \( OBD \).

Step 2.1: Find the area of triangle \( OBD \)

The area of a triangle can be calculated using the formula:
\( \text{Area of Triangle} = \frac{1}{2} \times \text{base} \times \text{height} \)

In triangle \( OBD \):
- Base \( OB = 3.5 \, \text{cm} \) (radius)
- Height \( OD = 2 \, \text{cm} \)

Substituting these values:
\( \text{Area of Triangle} = \frac{1}{2} \times OB \times OD = \frac{1}{2} \times 3.5 \times 2 \)

Calculating:
\( \text{Area of Triangle} = \frac{1}{2} \times 7 = 3.5 \, \text{cm}^2 \)

Step 2.2: Calculate the area of the shaded region

Now, we can find the area of the shaded region:
\( \text{Area of Shaded Region} = \text{Area of Quadrant} - \text{Area of Triangle} \)
Substituting the values:
\( \text{Area of Shaded Region} = 9.625 - 3.5 = 6.125 \, \text{cm}^2 \)

Final Answers:
(i) Area of the quadrant \( OACB = 9.625 \, \text{cm}^2 \)

(ii) Area of the shaded region = \( 6.125 \, \text{cm}^2 \)

---