ABCD is a cyclic trapezium with AD∣∣BC. If ∠B=700, determine other three angles of the trapezium.
To solve the problem, we need to find the angles of the cyclic trapezium ABCD, given that AD is parallel to BC and angle B is 70 degrees.
1. Identify the Given Information:
- We know that ABCD is a cyclic trapezium.
- AD is parallel to BC.
- Angle B = 70 degrees.
2. Use the Property of Cyclic Quadrilaterals:
- In a cyclic quadrilateral, opposite angles are supplementary. This means:
Angle B+Angle D=180∘
- Therefore, we can write:
70∘+Angle D=180∘
3. Calculate Angle D:
- Rearranging the equation gives:
Angle D=180∘−70∘=110∘
4. Use the Property of Parallel Lines:
- Since AD is parallel to BC, and AB is a transversal, we can use the property of consecutive interior angles:
Angle A+Angle B=180∘
- Substituting the value of Angle B:
Angle A+70∘=180∘
5. Calculate Angle A:
- Rearranging gives:
Angle A=180∘−70∘=110∘
6. Find Angle C Using the Cyclic Quadrilateral Property Again:
- Since opposite angles are supplementary:
Angle A+Angle C=180∘
- Substituting the value of Angle A:
110∘+Angle C=180∘
7. Calculate Angle C:
- Rearranging gives:
Angle C=180∘−110∘=70∘
Summary of Angles:
- Angle A = 110 degrees
- Angle B = 70 degrees
- Angle C = 70 degrees
- Angle D = 110 degrees
Final Answer:
The angles of the cyclic trapezium ABCD are:
- Angle A = 110°
- Angle B = 70°
- Angle C = 70°
- Angle D = 110°
- We know that ABCD is a cyclic trapezium.
- AD is parallel to BC.
- Angle B = 70 degrees.
- In a cyclic quadrilateral, opposite angles are supplementary. This means:
Angle B+Angle D=180∘
- Therefore, we can write:
70∘+Angle D=180∘
- Rearranging the equation gives:
Angle D=180∘−70∘=110∘
- Since AD is parallel to BC, and AB is a transversal, we can use the property of consecutive interior angles:
Angle A+Angle B=180∘
- Substituting the value of Angle B:
Angle A+70∘=180∘
- Rearranging gives:
Angle A=180∘−70∘=110∘
- Since opposite angles are supplementary:
Angle A+Angle C=180∘
- Substituting the value of Angle A:
110∘+Angle C=180∘
- Rearranging gives:
Angle C=180∘−110∘=70∘
- Angle A = 110 degrees
- Angle B = 70 degrees
- Angle C = 70 degrees
- Angle D = 110 degrees
The angles of the cyclic trapezium ABCD are:
- Angle A = 110°
- Angle B = 70°
- Angle C = 70°
- Angle D = 110°
Topper's Solved these Questions
Similar Questions
ABCD is a cyclic trapezium m, in which AB∣∣DC. If ∠B=75∘ , then find other angles.
View SolutionABCD is a cyclic trapezium in which, AD| |BC and ∠B=70∘. Find its remaining angles,
View SolutionIn a ABC, if ∠A=450 and ∠B=700. Determine the shortest and largest sides of the triangle.
View SolutionIn Fig. 4.170, ABCD is a trapezium in which AB∥DC and AB=2 DC . Determine the ratio of the areas of AOB and COD . (FIGURE)
View SolutionIn the given figure, ABCD is a trapezium with angle C=120∘,DC=28 cm and BC=40 cm. Find :
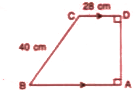
(iii) the area of the trapezium.
View SolutionIn a parallelogram ABCD, if ∠D=1350, determine the measures of its other angles.
View SolutionIn a cyclic quadrilateral ABCD, if AB || CD and ∠B=700, find the remaining angles.
View SolutionABCD is a trapezium in which AB∣∣DCand∠A=∠B=45∘. Find angles C and D of the trapezium.
View SolutionABCD is a rectangle with ∠ABD=400. Determine ∠DBC
View SolutionIn ABC, if ∠A=400and ∠B=600. Determine the longest and shortest sides of the triangle.
View Solution
