In the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
To determine which vectors are equal in the regular hexagon ABCDEF, we will analyze the vectors based on their directions and magnitudes.
1. Identify the Vectors:
In a regular hexagon, we can denote the vectors as follows:
- Let vector a represent the vector from point A to point B.
- Let vector b represent the vector from point B to point C.
- Let vector c represent the vector from point C to point D.
- Let vector d represent the vector from point D to point E.
- Let vector e represent the vector from point E to point F.
- Let vector f represent the vector from point F to point A.
2. Check Opposite Vectors:
- Vectors a and d are opposite in direction (as they point away from each other), hence they are not equal.
- Vectors b and e are also opposite in direction, hence they are not equal.
- Vectors c and f are also opposite in direction, hence they are not equal.
3. Check Adjacent Vectors:
- Vectors a and b are adjacent and point in different directions, hence they are not equal.
- Vectors b and c are adjacent and point in different directions, hence they are not equal.
- Vectors c and d are adjacent and point in different directions, hence they are not equal.
- Vectors d and e are adjacent and point in different directions, hence they are not equal.
- Vectors e and f are adjacent and point in different directions, hence they are not equal.
- Vectors f and a are adjacent and point in different directions, hence they are not equal.
4. Check for Equal Vectors:
- Vectors c and e are in the same direction and have the same magnitude since they are both sides of the regular hexagon. Therefore, c = e.
- Vectors u and v (assuming these represent specific vectors in the hexagon) are also in the same direction and have the same magnitude, hence u = v.
Conclusion:
From our analysis, we conclude that:
- The pairs of equal vectors are:
- Vector c = Vector e
- Vector u = Vector v
In a regular hexagon, we can denote the vectors as follows:
- Let vector a represent the vector from point A to point B.
- Let vector b represent the vector from point B to point C.
- Let vector c represent the vector from point C to point D.
- Let vector d represent the vector from point D to point E.
- Let vector e represent the vector from point E to point F.
- Let vector f represent the vector from point F to point A.
- Vectors a and d are opposite in direction (as they point away from each other), hence they are not equal.
- Vectors b and e are also opposite in direction, hence they are not equal.
- Vectors c and f are also opposite in direction, hence they are not equal.
- Vectors a and b are adjacent and point in different directions, hence they are not equal.
- Vectors b and c are adjacent and point in different directions, hence they are not equal.
- Vectors c and d are adjacent and point in different directions, hence they are not equal.
- Vectors d and e are adjacent and point in different directions, hence they are not equal.
- Vectors e and f are adjacent and point in different directions, hence they are not equal.
- Vectors f and a are adjacent and point in different directions, hence they are not equal.
- Vectors c and e are in the same direction and have the same magnitude since they are both sides of the regular hexagon. Therefore, c = e.
- Vectors u and v (assuming these represent specific vectors in the hexagon) are also in the same direction and have the same magnitude, hence u = v.
From our analysis, we conclude that:
- The pairs of equal vectors are:
- Vector c = Vector e
- Vector u = Vector v
Similar Questions
In the given figure ABCDEF is a regular hexagon. Examine which vector are, Collinear but not equal
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, collinear
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Cointial
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
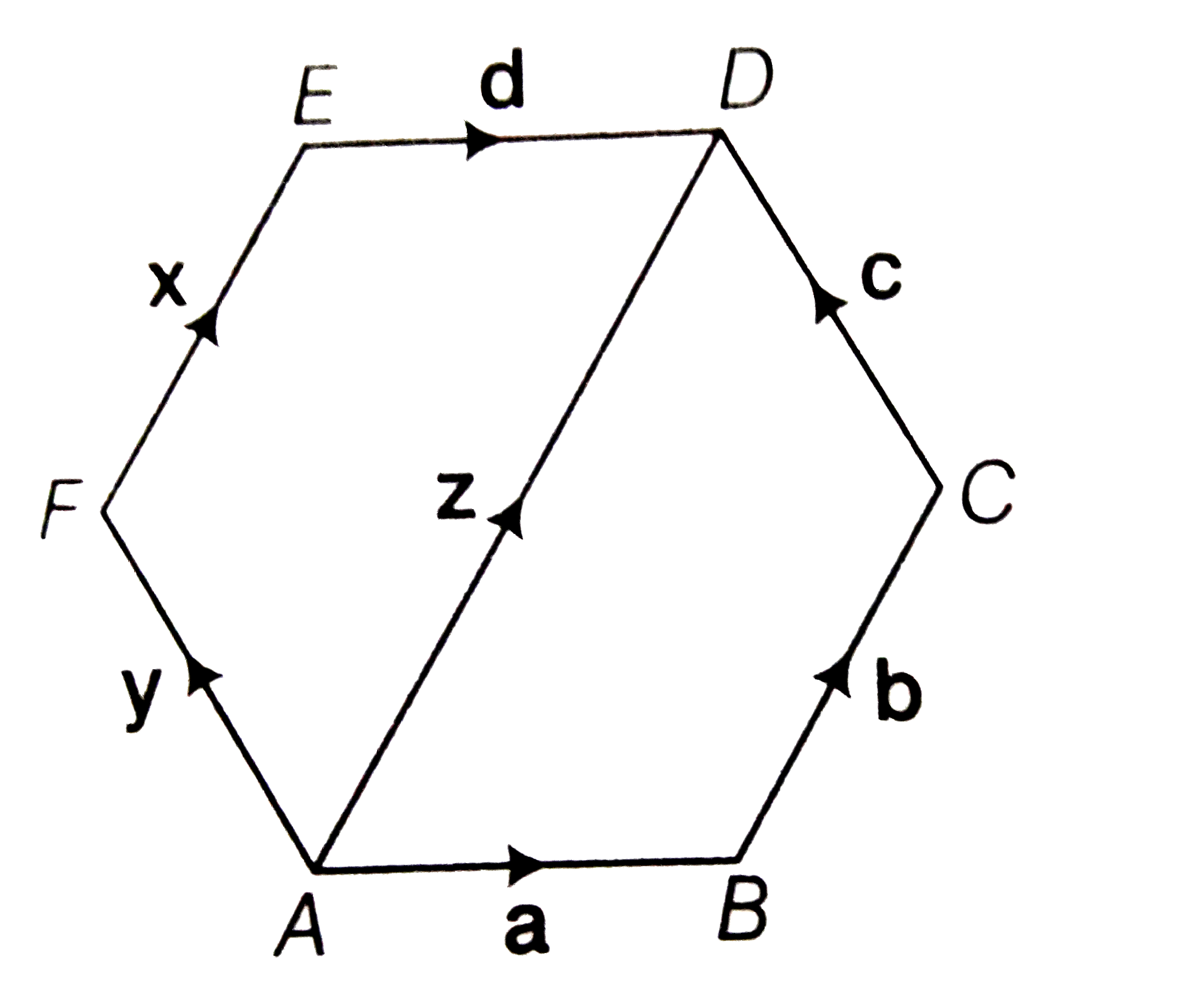
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear but not equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: coinitial
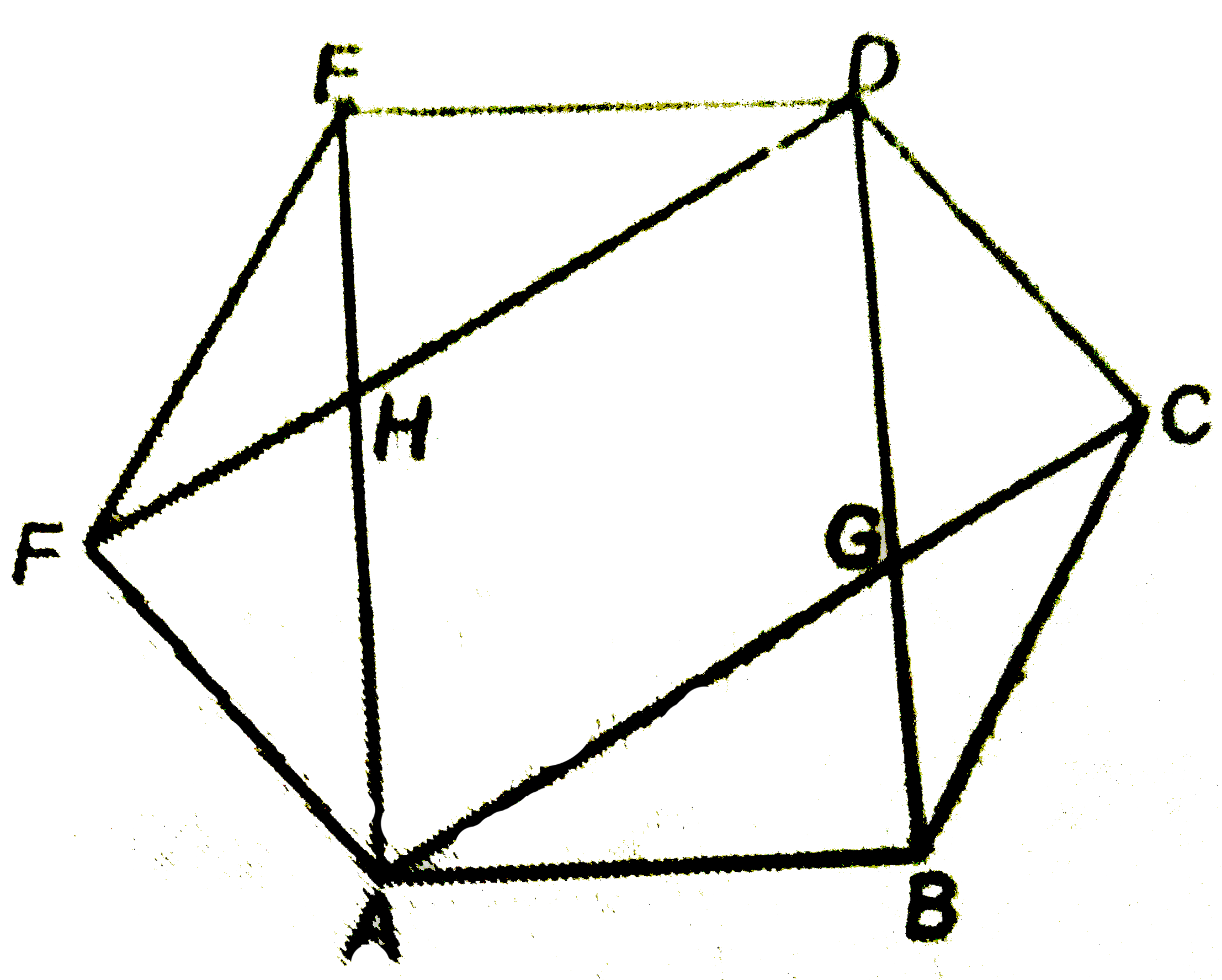
View SolutionIn the adjoining figure, ABCDEF is a regular hexagon. Prove that □ABDE,□ACDFand□AGDH are parallelograms.
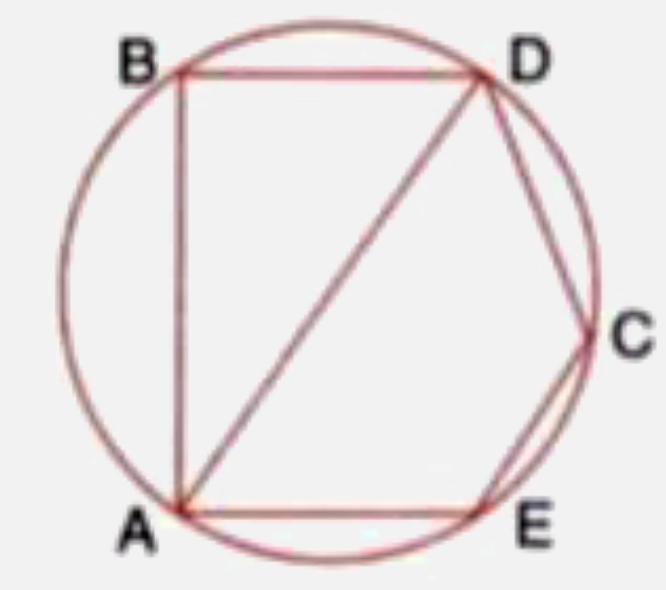
View SolutionIn the given figure , BD is a side of a regular hexagon. DC is a side of a regular pentagon and AD is a diameter , Calculate:
(i) ∠ADC,
(ii) ∠BDA
(iii) ∠ABC
(iv)∠AEC
View Solution
