In the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear but not equal
To solve the problem of determining which vectors are collinear but not equal in the rectangle ABCD, we will follow these steps:
Step 1: Identify the Vectors
In rectangle ABCD, we have four vectors:
- Vector A (AB)
- Vector B (CD)
- Vector C (AD)
- Vector D (BC)
Step 2: Check for Collinearity
Vectors are said to be collinear if they are parallel to each other. In a rectangle:
- Vector A (AB) is parallel to Vector B (CD) because they are opposite sides of the rectangle.
- Vector C (AD) is parallel to Vector D (BC) because they are also opposite sides of the rectangle.
Thus, we can conclude that:
- Vector A is collinear with Vector B.
- Vector C is collinear with Vector D.
Step 3: Check for Equality
For vectors to be equal, they must have the same magnitude and direction. In a rectangle:
- The magnitudes of Vector A and Vector B are equal since they are opposite sides of the rectangle, but they point in opposite directions. Therefore, Vector A is not equal to Vector B.
- Similarly, the magnitudes of Vector C and Vector D are equal, and they point in the same direction. Thus, Vector C is equal to Vector D.
Conclusion
From the above analysis, we find that:
- Vectors A and B are collinear but not equal.
- Vectors C and D are equal.
Final Answer
The vectors that are collinear but not equal are:
- Vector A and Vector B.
---
In rectangle ABCD, we have four vectors:
- Vector A (AB)
- Vector B (CD)
- Vector C (AD)
- Vector D (BC)
Vectors are said to be collinear if they are parallel to each other. In a rectangle:
- Vector A (AB) is parallel to Vector B (CD) because they are opposite sides of the rectangle.
- Vector C (AD) is parallel to Vector D (BC) because they are also opposite sides of the rectangle.
- Vector A is collinear with Vector B.
- Vector C is collinear with Vector D.
For vectors to be equal, they must have the same magnitude and direction. In a rectangle:
- The magnitudes of Vector A and Vector B are equal since they are opposite sides of the rectangle, but they point in opposite directions. Therefore, Vector A is not equal to Vector B.
- Similarly, the magnitudes of Vector C and Vector D are equal, and they point in the same direction. Thus, Vector C is equal to Vector D.
From the above analysis, we find that:
- Vectors A and B are collinear but not equal.
- Vectors C and D are equal.
The vectors that are collinear but not equal are:
- Vector A and Vector B.
Similar Questions
In the adjoining figure ABCD is a rectangle . Examine which of the vector are: equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: coinitial
View SolutionIn the adjoining figure find ∠x
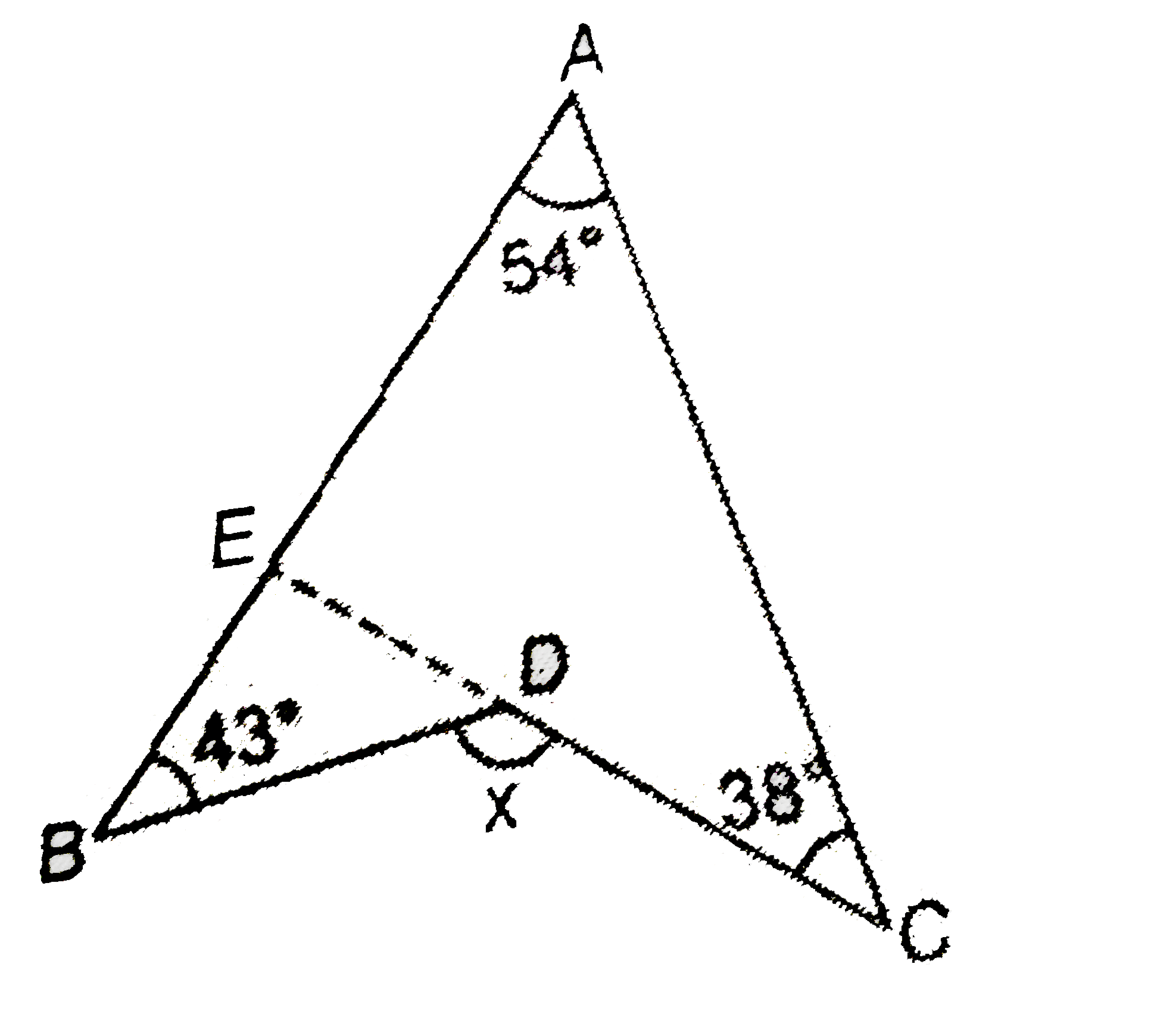
View SolutionIn the adjoining figure find ∠x
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Collinear but not equal
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, collinear
View SolutionIn the adjoining figure which of the vector are: collinear

View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, Cointial
View Solutionin the adjoining figure find ∠F.
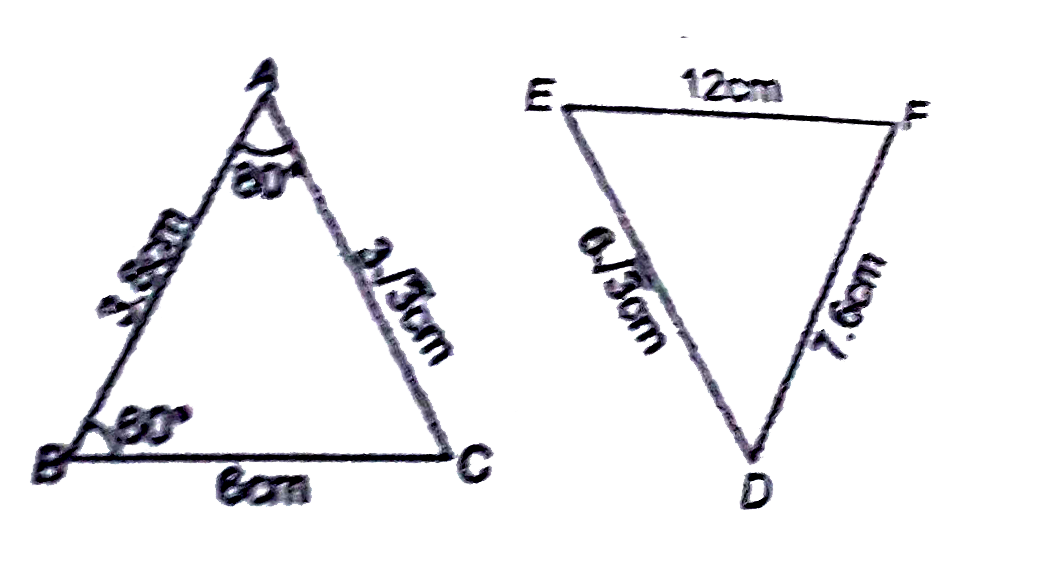
View Solution
