In the given figure ABCDEF is a regular hexagon. Examine which vector are, Collinear but not equal
To determine which vectors in the regular hexagon ABCDEF are collinear but not equal, we can follow these steps:
Step 1: Identify the Vectors
In a regular hexagon, we can represent the vertices as vectors:
- Let →A represent the vector from the center to vertex A.
- Let →B represent the vector from the center to vertex B.
- Let →C represent the vector from the center to vertex C.
- Let →D represent the vector from the center to vertex D.
- Let →E represent the vector from the center to vertex E.
- Let →F represent the vector from the center to vertex F.
Step 2: Determine Collinearity
Two vectors are collinear if they are parallel to each other. In a regular hexagon:
- Opposite sides are parallel, which means the vectors representing these sides are collinear.
Step 3: List Collinear Vector Pairs
From the hexagon, we can identify the following pairs of collinear vectors:
1. →A and →D
2. →B and →E
3. →C and →F
4. →A and →B
5. →B and →C
6. →C and →D
7. →D and →E
8. →E and →F
9. →F and →A
Step 4: Check for Equality
Next, we need to check which of these pairs are not equal:
- Vectors are equal if they have the same magnitude and direction.
Step 5: Identify Collinear but Not Equal Vectors
1. →A and →D: Collinear (opposite directions), not equal.
2. →B and →E: Collinear (opposite directions), not equal.
3. →C and →F: Collinear (opposite directions), not equal.
4. →A and →B: Collinear (adjacent sides), not equal.
5. →B and →C: Collinear (adjacent sides), not equal.
6. →C and →D: Collinear (adjacent sides), not equal.
7. →D and →E: Collinear (adjacent sides), not equal.
8. →E and →F: Collinear (adjacent sides), not equal.
9. →F and →A: Collinear (adjacent sides), not equal.
Final Result
The pairs of vectors that are collinear but not equal are:
- →A and →D
- →B and →E
- →C and →F
In a regular hexagon, we can represent the vertices as vectors:
- Let →A represent the vector from the center to vertex A.
- Let →B represent the vector from the center to vertex B.
- Let →C represent the vector from the center to vertex C.
- Let →D represent the vector from the center to vertex D.
- Let →E represent the vector from the center to vertex E.
- Let →F represent the vector from the center to vertex F.
Two vectors are collinear if they are parallel to each other. In a regular hexagon:
- Opposite sides are parallel, which means the vectors representing these sides are collinear.
From the hexagon, we can identify the following pairs of collinear vectors:
1. →A and →D
2. →B and →E
3. →C and →F
4. →A and →B
5. →B and →C
6. →C and →D
7. →D and →E
8. →E and →F
9. →F and →A
Next, we need to check which of these pairs are not equal:
- Vectors are equal if they have the same magnitude and direction.
1. →A and →D: Collinear (opposite directions), not equal.
2. →B and →E: Collinear (opposite directions), not equal.
3. →C and →F: Collinear (opposite directions), not equal.
4. →A and →B: Collinear (adjacent sides), not equal.
5. →B and →C: Collinear (adjacent sides), not equal.
6. →C and →D: Collinear (adjacent sides), not equal.
7. →D and →E: Collinear (adjacent sides), not equal.
8. →E and →F: Collinear (adjacent sides), not equal.
9. →F and →A: Collinear (adjacent sides), not equal.
The pairs of vectors that are collinear but not equal are:
- →A and →D
- →B and →E
- →C and →F
Similar Questions
In the given figure ABCDEF is a regular hexagon. Examine which vector are, Cointial
View SolutionIn the given figure ABCDEF is a regular hexagon. Examine which vector are, equal
View SolutionIn the given figure, ABCDEF is a regular hexagon, which vectors are:
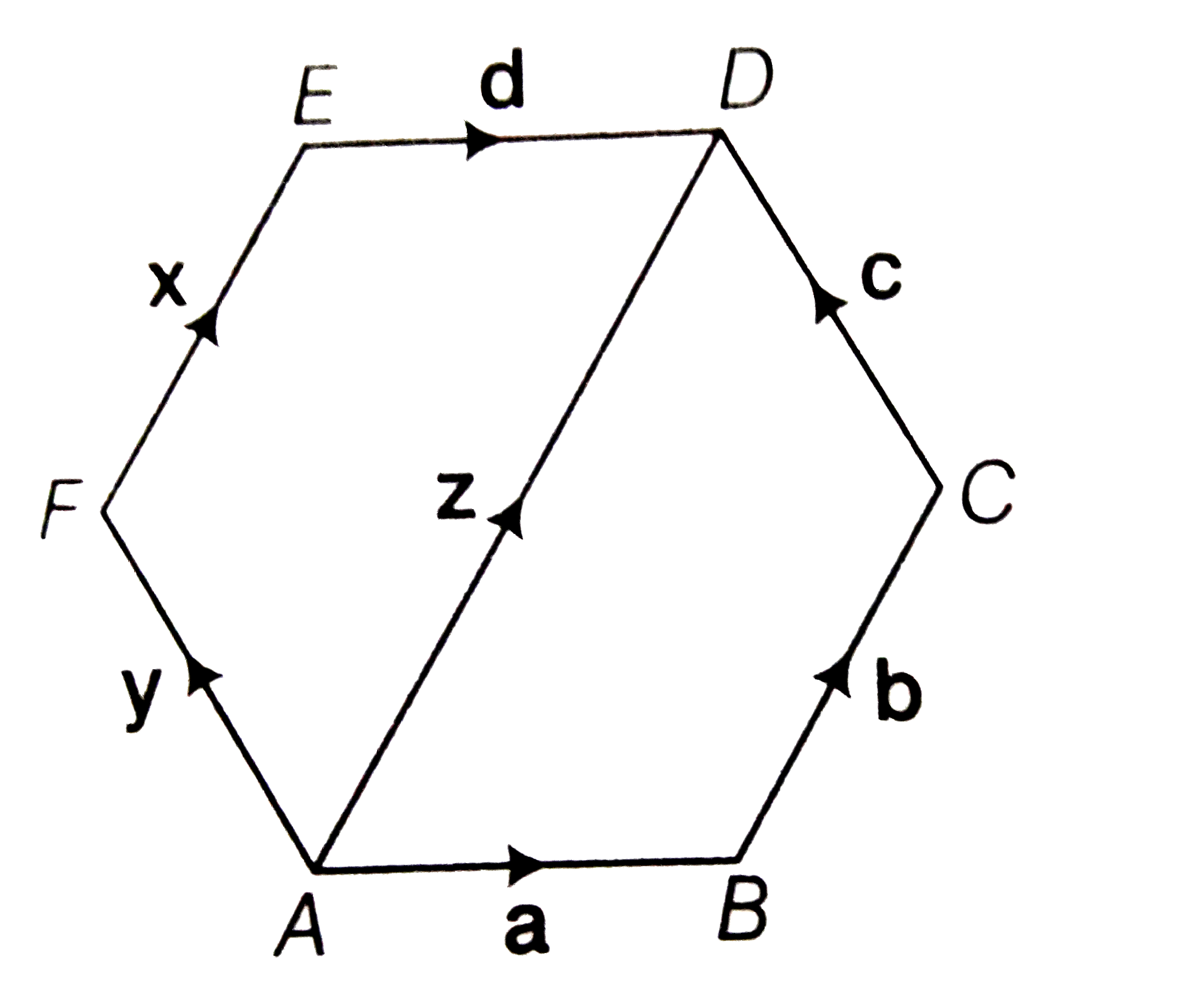
(i) Collinear
(ii) Equal
(iii) Coinitial
(iv) Collinear but not equal.
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear but not equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: collinear
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: equal
View SolutionIn the adjoining figure ABCD is a rectangle . Examine which of the vector are: coinitial
View SolutionIn Fig. ABCD is a regular hexagon, which vectors are: (i) Collinear (ii) Equal (iii) Coinitial (iv) Collinear but not equal
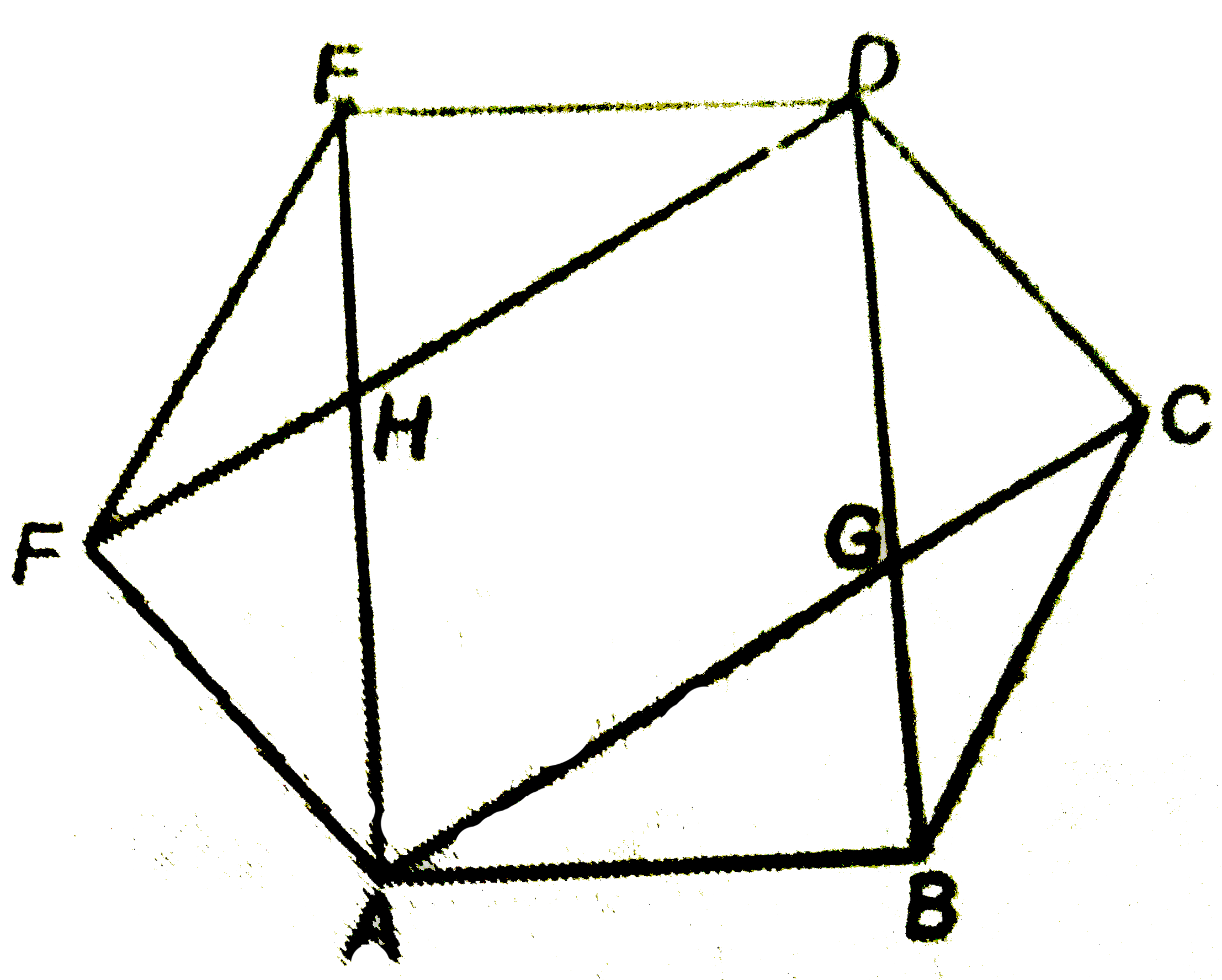
View SolutionIn the adjoining figure, ABCDEF is a regular hexagon. Prove that □ABDE,□ACDFand□AGDH are parallelograms.
View SolutionIn the given figure, AB is a side of a regular hexagon and AC is a side of a regular eight sided polygon. Find :
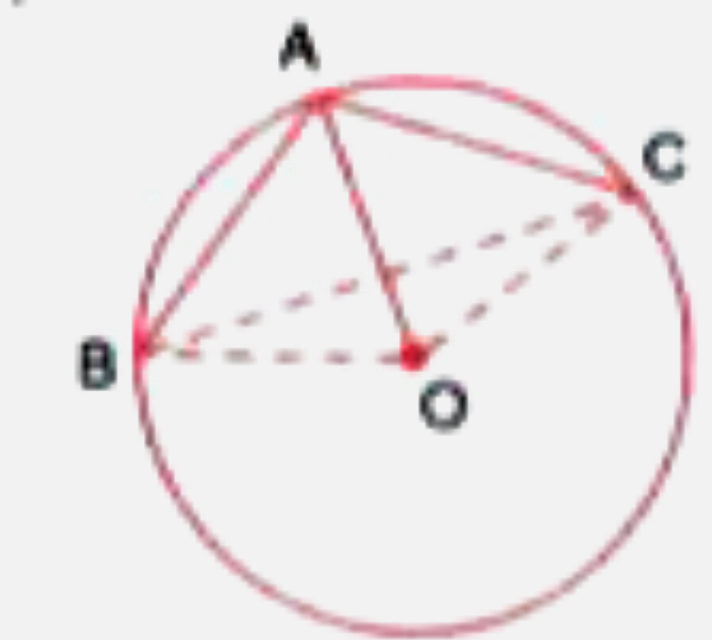
∠BOC
View Solution
