In the given figure, and are parallel lines intersected by a transversal at and respectively, If find all other angles in the figure.
To solve the problem step by step, we will use the properties of angles formed by parallel lines and a transversal.
1. Identify Given Information:
- We have two parallel lines AB and CD.
- A transversal PQ intersects AB at point L and CD at point M.
- We are given that ∠CMQ=60∘.
2. Find Angle 1:
- ∠CMQ and ∠1 form a linear pair (they are on a straight line).
- Therefore, ∠1+∠CMQ=180∘.
- Substitute ∠CMQ=60∘:
∠1+60∘=180∘
- Solving for ∠1:
∠1=180∘−60∘=120∘
3. Find Angle 2:
- ∠CMQ and ∠2 are vertically opposite angles.
- Therefore, ∠2=∠CMQ=60∘.
4. Find Angle 3:
- ∠1 and ∠3 are also vertically opposite angles.
- Therefore, ∠3=∠1=120∘.
5. Find Angle 4:
- ∠CMQ and ∠4 are corresponding angles.
- Therefore, ∠4=∠CMQ=60∘.
6. Find Angle 5:
- ∠1 and ∠5 are corresponding angles.
- Therefore, ∠5=∠1=120∘.
7. Find Angle 6:
- ∠2 and ∠6 are corresponding angles.
- Therefore, ∠6=∠2=60∘.
8. Find Angle 7:
- ∠3 and ∠7 are corresponding angles.
- Therefore, ∠7=∠3=120∘.
Summary of Angles:
- ∠1=120∘
- ∠2=60∘
- ∠3=120∘
- ∠4=60∘
- ∠5=120∘
- ∠6=60∘
- ∠7=120∘
- We have two parallel lines AB and CD.
- A transversal PQ intersects AB at point L and CD at point M.
- We are given that ∠CMQ=60∘.
- ∠CMQ and ∠1 form a linear pair (they are on a straight line).
- Therefore, ∠1+∠CMQ=180∘.
- Substitute ∠CMQ=60∘:
∠1+60∘=180∘
- Solving for ∠1:
∠1=180∘−60∘=120∘
- ∠CMQ and ∠2 are vertically opposite angles.
- Therefore, ∠2=∠CMQ=60∘.
- ∠1 and ∠3 are also vertically opposite angles.
- Therefore, ∠3=∠1=120∘.
- ∠CMQ and ∠4 are corresponding angles.
- Therefore, ∠4=∠CMQ=60∘.
- ∠1 and ∠5 are corresponding angles.
- Therefore, ∠5=∠1=120∘.
- ∠2 and ∠6 are corresponding angles.
- Therefore, ∠6=∠2=60∘.
- ∠3 and ∠7 are corresponding angles.
- Therefore, ∠7=∠3=120∘.
- ∠1=120∘
- ∠2=60∘
- ∠3=120∘
- ∠4=60∘
- ∠5=120∘
- ∠6=60∘
- ∠7=120∘
Topper's Solved these Questions
Similar Questions
In the given figure, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionIn the given figure l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIn the given figure, AB||CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
View SolutionIn Fig. l, m and n are parallel lines intersected by transversal P at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
View SolutionIn the given figure, line l || m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
View SolutionIn Figure, l, m and n are parallel lines intersected by a transversal at X, Y, and Z respectively. Find ∠1, ∠2 and ∠3. Give reasons.
View SolutionIn Fig. 51, l, m and n are parallel lines intersected by a transversal p at X,Y and Z respectively. Find ∠1, ∠2 and ∠3. Give reasons.
View SolutionIn the given figure l||mandp||q. Find the angle x,y, z
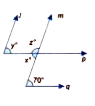
View SolutionIn the given figure, l||mandp||q. Find the angles x, y and z

View SolutionIn the given figure, l||m||nandp||q||r. Find the angles x,y, z and t.
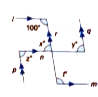
View Solution
