In Fig.66, if AFDE, then x= 37 (b) 57 47 (d) 67
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
1. Identify the Given Information:
- We have two parallel lines, AF and DE.
- We know that angle CAX = 24 degrees and angle EDC = 109 degrees.
2. Use the Property of Parallel Lines:
- Since AF is parallel to DE and DC is a transversal, we can use the property that states the sum of the interior angles on the same side of the transversal is equal to 180 degrees.
- Therefore, we can write the equation:
Angle EDC+Angle 1=180∘
3. Substitute the Known Value:
- We know angle EDC = 109 degrees, so we substitute this into our equation:
109∘+Angle 1=180∘
4. Solve for Angle 1:
- Rearranging the equation gives us:
Angle 1=180∘−109∘=71∘
5. Apply the Exterior Angle Property:
- In triangle ACX, angle 1 (which we found to be 71 degrees) is an exterior angle. The exterior angle is equal to the sum of the two opposite interior angles.
- Therefore, we can write:
Angle 1=Angle CAX+Angle CXA
- Substituting the known values gives us:
71∘=24∘+X
6. Solve for X:
- Rearranging the equation to isolate X gives us:
X=71∘−24∘=47∘
7. Final Answer:
- The value of X is 47 degrees.
Summary:
Thus, the answer to the question is X=47∘.
- We have two parallel lines, AF and DE.
- We know that angle CAX = 24 degrees and angle EDC = 109 degrees.
- Since AF is parallel to DE and DC is a transversal, we can use the property that states the sum of the interior angles on the same side of the transversal is equal to 180 degrees.
- Therefore, we can write the equation:
Angle EDC+Angle 1=180∘
- We know angle EDC = 109 degrees, so we substitute this into our equation:
109∘+Angle 1=180∘
- Rearranging the equation gives us:
Angle 1=180∘−109∘=71∘
- In triangle ACX, angle 1 (which we found to be 71 degrees) is an exterior angle. The exterior angle is equal to the sum of the two opposite interior angles.
- Therefore, we can write:
Angle 1=Angle CAX+Angle CXA
- Substituting the known values gives us:
71∘=24∘+X
- Rearranging the equation to isolate X gives us:
X=71∘−24∘=47∘
- The value of X is 47 degrees.
Thus, the answer to the question is X=47∘.
Topper's Solved these Questions
Similar Questions
In Fig. 4.246, if PBCF and DPEF , then ADDE= (FIGURE) 34 (b) 13 (c) 14 (d) 23
View SolutionIn Fig. if AB∣∣CD , find the value of x .
View SolutionIn Fig.71, if ABCD, then the values of x, y and z are x=56, y=47, z=77 (b) x=47, y=56, z=77 x=77, y=56, z=47 (d) x=56, y=77, z=47
View SolutionIn Fig. AB∣∣DC . Find the value of x
View SolutionIn Figure, for which value of x is l1l2 ? 37 (b) 43 (c) 45 (d) 47
View SolutionIn Fig.72, if AB∣∣CD and AE∣∣BD, then the value of x
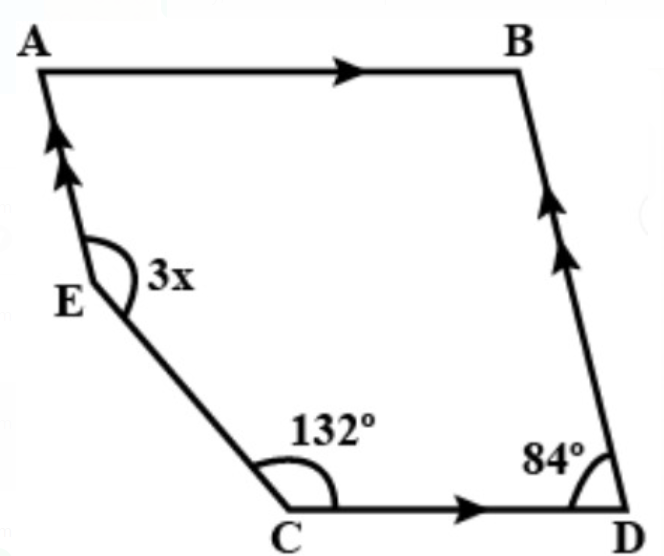 is
(a) 38 (b) 48
(b) 58 (d) 68
is
(a) 38 (b) 48
(b) 58 (d) 68
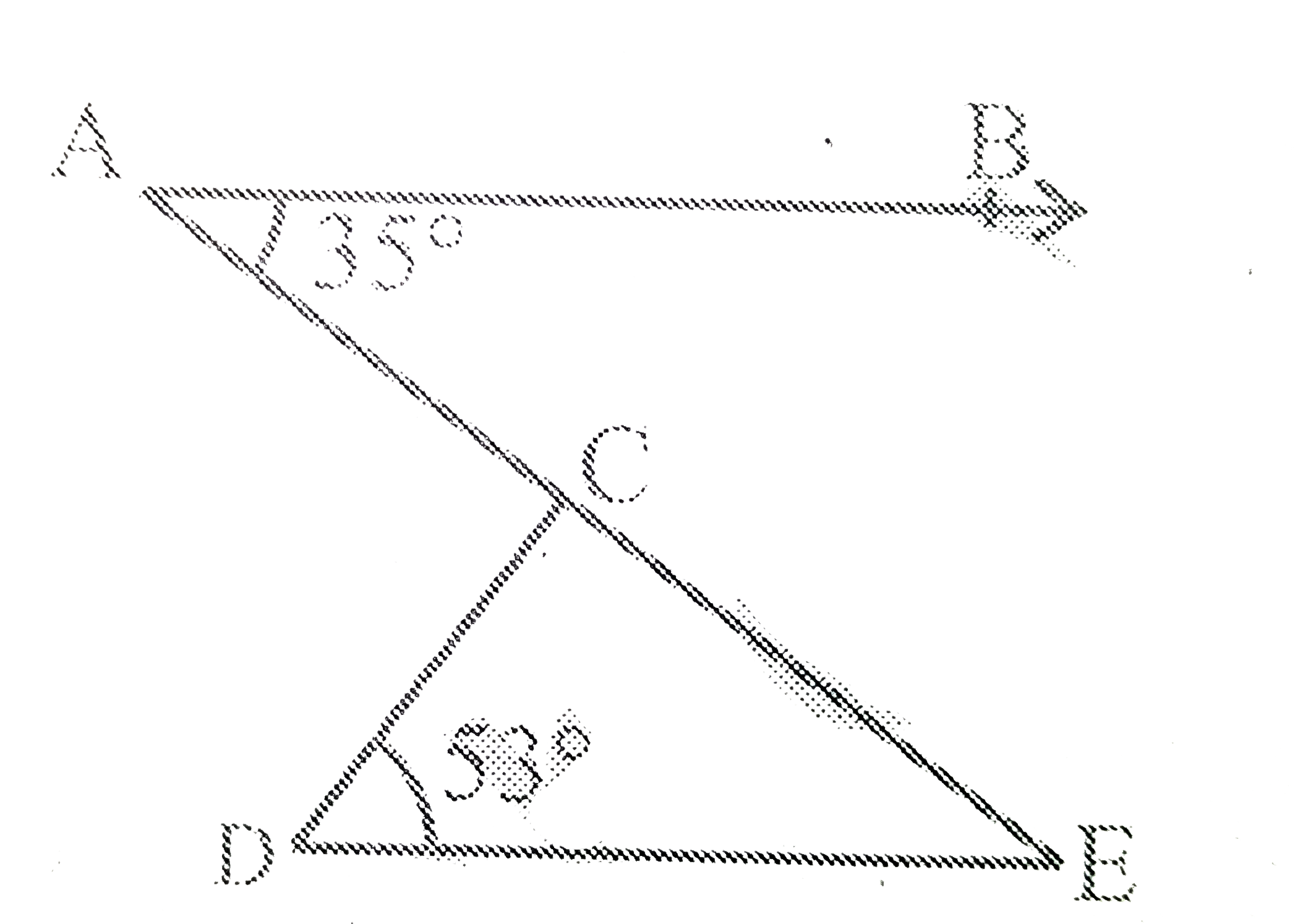
View SolutionIn Fig. 6.41, if AB∣∣DE,∠BAC=35∘ and ∠CDE=53∘, find ∠DCE.
View SolutionIn Fig.95, If AB, CD and EF are straight lines, then x= (a) 5 (b) 10 (c) 20 (d) 30
View SolutionIn Fig. 4.89, if EDC~EBA, ∠BEC=115o and ∠EDC=70o . Find ∠DEC, ∠DCE, ∠EAB, ∠AEB and ∠EBA . (FIGURE)
View SolutionIn Figure, if AB||HF and DE||FG , then the measure of ∠FDE is (a) 1080 (b) 800 (c) 1000 (d) 900
View Solution
