In figure, if , show that .

Given,
Hence, by CPCT. .....(1)
[CPTC: corresponding parts of congruent triangles]
and by CPCT.
.....(2)
Dividing (2) by (1)
....(3)
In and
(common angle)
from (3)
∴ is similar to by SAS criterion.
Hence proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.2
10 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLES
14 Videos
- TRIANGLESBOOK - NCERT ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 6.5
17 Videos
- SURFACE AREAS AND VOLUMESBOOK - NCERT ENGLISHCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - Exercise 13.3
9 Videos
Similar Questions
Δ ABC and Δ ABD are on a common base AB, and AC = BD and BC = AD as shown in Fig. 18. Which of the following statements is true? ΔABC≅ΔABD ΔABC≅ΔADB ΔABC≅ΔBAD
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that: (i) ΔAMC~ΔPNR (ii) CMRN=ABPQ (ii) ΔCMB~ΔRNQ
View SolutionIn Figure, if △ABE≅△ACD , prove that △ADE~△ABC .
View SolutionΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
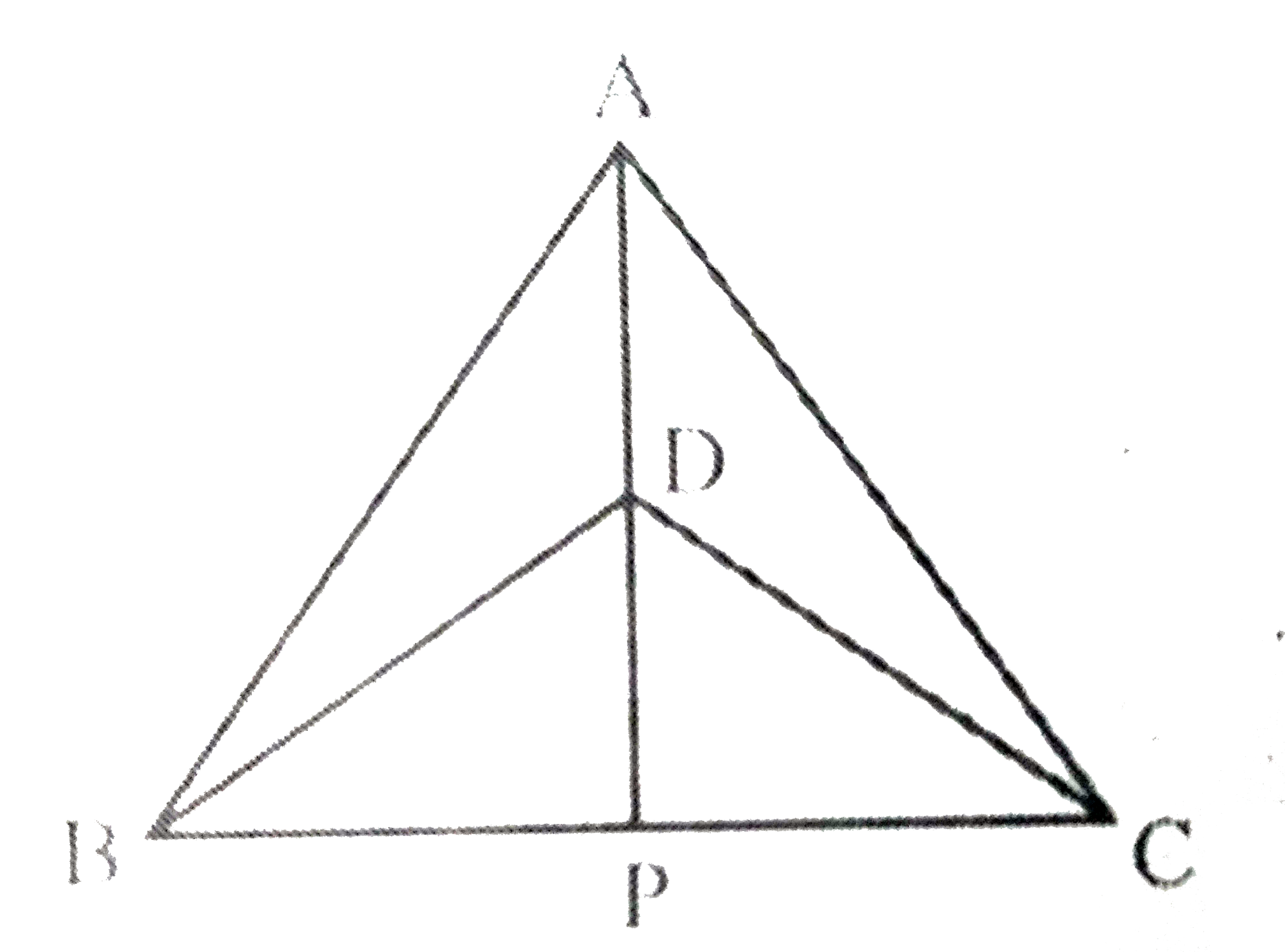
View SolutionIn Figure altitudes AD and CE of A B C intersect each other at the point P. Show that:(i) ΔAEP~ΔCDP (ii) ΔABD~ΔCBE (iii) ΔAEP~ΔADB(iv) ΔPDC~ΔBEC
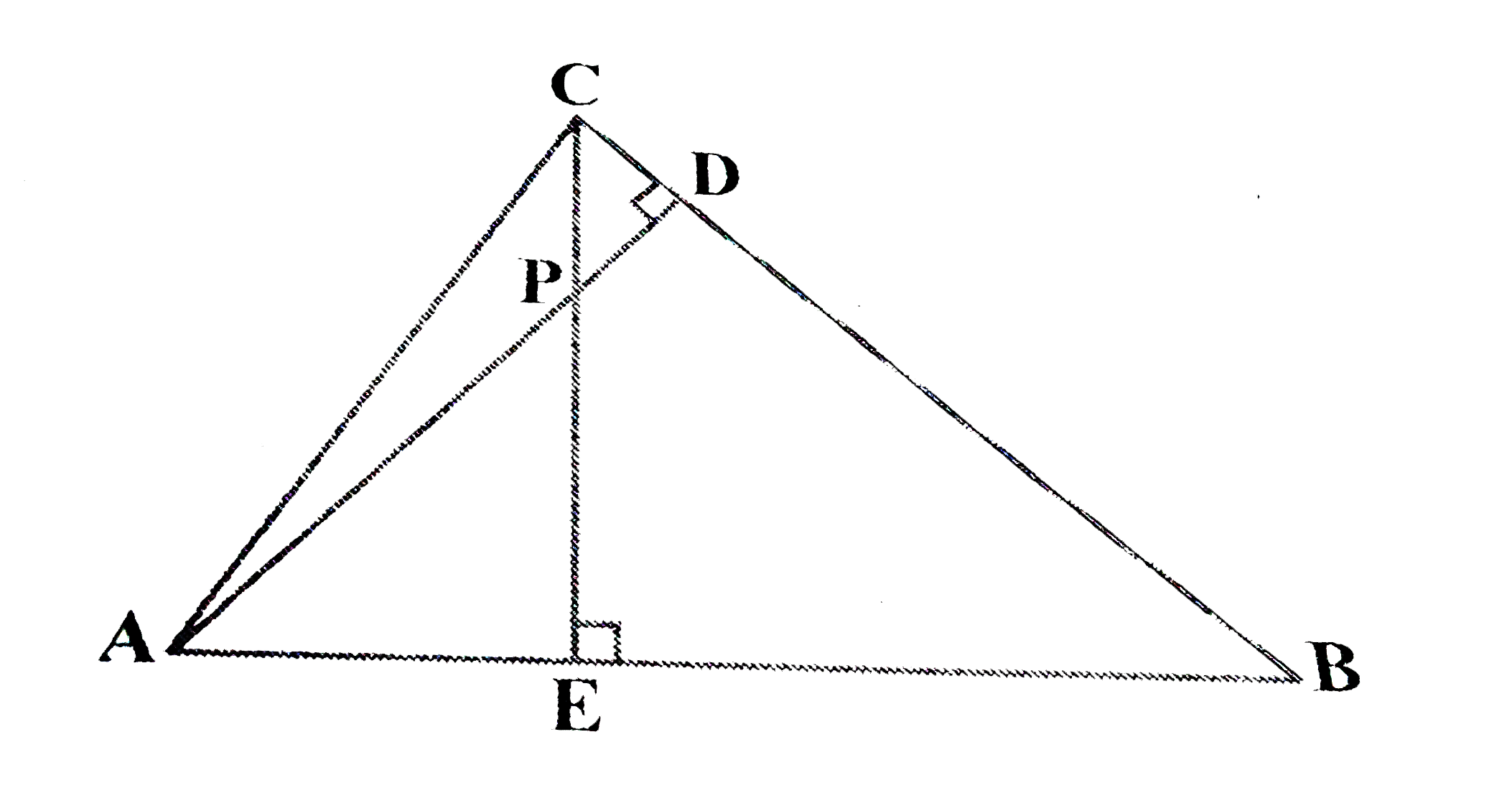
View SolutionSides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of ΔPQR. Show that ΔABC~ΔPQR.
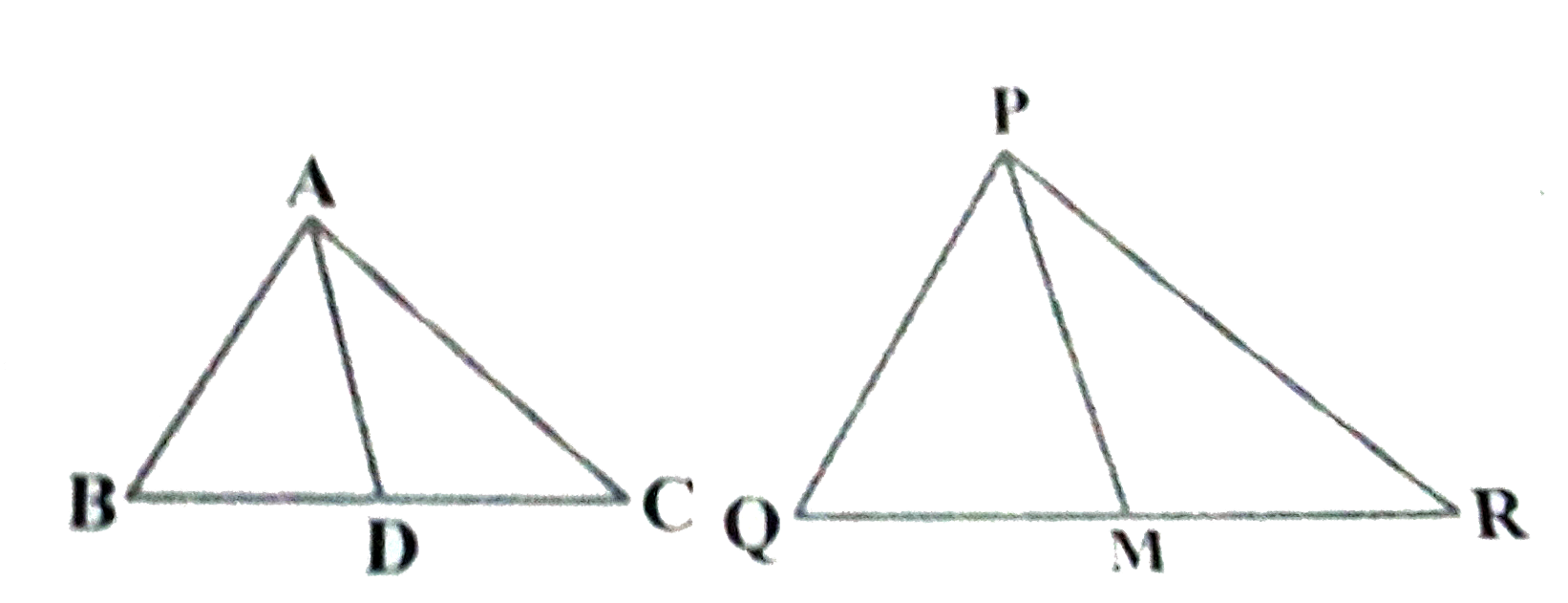
View SolutionIn figure.20,ΔABC is isosceles with AB=AC. State ifΔABC≅ΔACB. If yes, state three relations that you use to arrive at your answer.
View SolutionE is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that ΔABE~ΔCFB.
View SolutionIn figure, AB∣∣DC and AB=DC. (i)IsΔACD≅ΔCAB? (ii)State the three pairs of matching parts used to answer (iii) Which angle is equal to∠CAD ? (iv) Does it follow from (iii) that A D || B C ?
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN aresquares on the sides BC, CA and AB respectively. Line segment AX⊥DEmeets BCat Y. Show that:(i) ΔMBC≅ΔABD(ii) a r\ (B Y X D)\ =\ 2\
View Solution
