ΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC
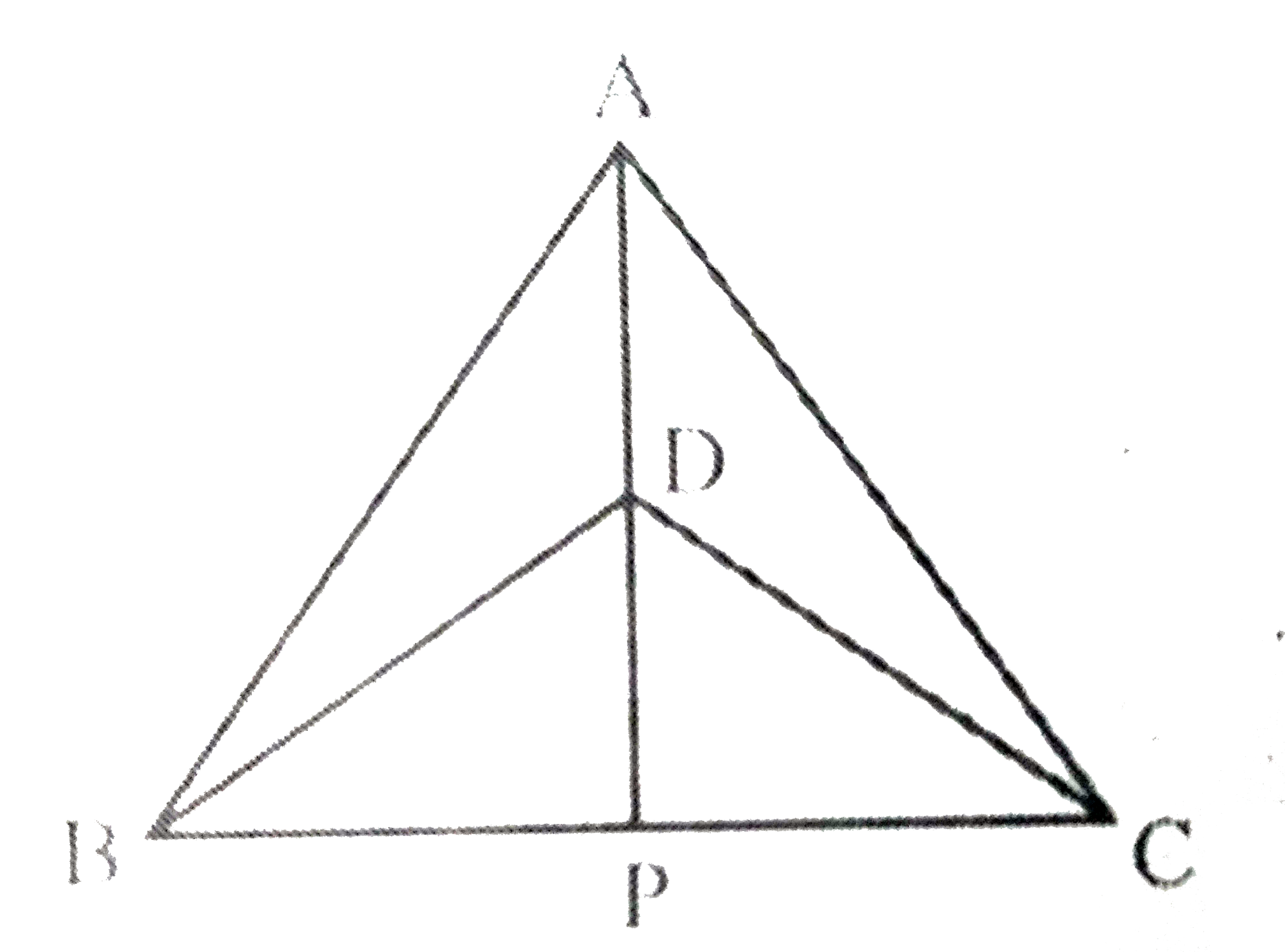
(##IX07_E0301_s01##)
(i) In ΔABD and ΔACD,
AB=AC (Equal sides of isosceles ΔABC)
BD=CD (Equal sides of isosceles ΔDBC)
AD=AD (Common)
ΔABD≅ΔACD (By SSS congruence rule)
By CPCT, we get
∠BAD=∠CAD
∠BAP=∠CAP…. (1)
∠ADB=∠ADC…. (2)
(ii) In ΔABP and ΔACP,
AB=AC (Given)
∠BAP=∠CAP [From equation (1)]
AP=AP (Common)
∴ ΔABP≅ΔACP (By SAS congruence rule)
∴BP=CP (By CPCT)…. (3)
(iii) From Equation (1) we know that ∠BAP = ∠CAP
Hence, AP is the angle bisector of ∠A.
From equation (2), we know that ∠ADB=∠ADC
⇒180∘−∠ADB=180∘−∠ADC
⇒∠BDP=∠CDP.... (4)
Hence, AP is the bisector of ∠D.
(iv) In ΔBDP and ΔCDP,
DP=DP (Common side)
∠BDP=∠CDP (Using (4))
DB=DC (Equal sides of isosceles ΔDBC)
∴ΔBDP≅ΔCDP (By SAS conguence rule)
∴ ∠BPD=∠CPD (By CPCT)…. (5)
∠BPD+∠CPD=180∘ (Linear pair angles)
∠BPD+∠BPD=180∘ [From Equation (5)]
∠BPD=90∘… (6)
Also, BP=CP [From equation (3)]
Similar Questions
Triangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
ΔABP≅ΔACP
View SolutionTriangles ABC and DBC are two isosceles triangles on the same base BC and their vertices A and D are on the same side of BC. If AD is extended to intersect BC at P, show that:
AP bisects angle BAC and BDC.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects ∠A as well as ∠D and AP is the perpendicular bisector of BC
View SolutionThe given figure shows two isosceles triangles ABC and DBC with common base BC. AD is extended to intersect BC at point P. Show that:
ΔABD=ΔACD
(ii) ΔABP=ΔACP
(iii) AP bisects ∠BDC
(iv) AP is perpendicular bisector of BC.
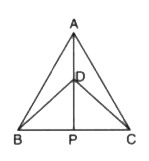
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
View SolutionABC and DBC are two triangle on the same base BC such that A and D lie on the opposite sides of BC,AB=AC and DB =DC ,Show that AD is the perpedicular bisector of BC.
View SolutionIn figure, if ΔABE≅ΔACD, show that ΔADE~ΔABC.

View SolutionIf ΔABC is an isosceles triangle such that AB=AC, then altitude AD from A on BC bisects BC (Fig.43).
View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View Solution