The human body has an average temperature of 98∘F. Assume that vapor pressure of the blood in the veins behaves like that of pure water. Find the minimum atmospheric pressure which is necessary to prevent the blood from boiling. Use figure for the vapor pressures.
To solve the problem of finding the minimum atmospheric pressure necessary to prevent the blood from boiling at an average human body temperature of 98°F, we can follow these steps:
Step 1: Convert Temperature from Fahrenheit to Celsius
We need to convert the temperature from Fahrenheit to Celsius because the vapor pressure data is typically provided in Celsius.
The formula to convert Fahrenheit (°F) to Celsius (°C) is:
T(°C)=59×(T(°F)−32)
Substituting the given temperature:
T(°C)=59×(98−32)=59×66=36.67°C
Step 2: Find the Saturation Vapor Pressure at 36.67°C
Next, we need to find the saturation vapor pressure of water at the calculated temperature of 36.67°C. This can typically be found using a vapor pressure table or graph.
From the graph, we can approximate the saturation vapor pressure at 36.67°C. For this example, we find that the saturation vapor pressure is approximately 50 mmHg.
Step 3: Determine the Minimum Atmospheric Pressure
To prevent the blood from boiling, the external atmospheric pressure must be equal to or greater than the saturation vapor pressure of the blood. Therefore, the minimum atmospheric pressure required is equal to the saturation vapor pressure we found in Step 2.
Thus, the minimum atmospheric pressure necessary to prevent the blood from boiling is:
Pmin=50 mmHg
Final Answer
The minimum atmospheric pressure necessary to prevent the blood from boiling is 50 mmHg.
---
We need to convert the temperature from Fahrenheit to Celsius because the vapor pressure data is typically provided in Celsius.
T(°C)=59×(T(°F)−32)
T(°C)=59×(98−32)=59×66=36.67°C
Next, we need to find the saturation vapor pressure of water at the calculated temperature of 36.67°C. This can typically be found using a vapor pressure table or graph.
To prevent the blood from boiling, the external atmospheric pressure must be equal to or greater than the saturation vapor pressure of the blood. Therefore, the minimum atmospheric pressure required is equal to the saturation vapor pressure we found in Step 2.
Pmin=50 mmHg
The minimum atmospheric pressure necessary to prevent the blood from boiling is 50 mmHg.
Topper's Solved these Questions
Similar Questions
Each phase of a material can exits only in certain regions of pressure and temperature . P−T phase diagrams, in which pressure is plotted versus temperature, show the regions corresponding to various phases and phase transformations . P−V diagrams, on the other hand , can be used to study pressure volume relationship at a constant temperature.
If the liquid and gaseous phases of a pure substances are heated together in a closed container, both the temperature and the vapor pressure will increase until a point is reached at which the two phases can no longer be distinguished from one another. The temperature and pressure at which this occurs are called the critical temperature and pressure. Exceeding either of these parameters, by itself ,will cause the gas/liguid phase transition to disappear. if the other variable is then changed as well, while the first variable is maintained above its critical point , a gradual transition will occur between the gaseous and liquid phases, with no clear boundary.(The liquid and solid phases, on the other hand , maintain a distinct boundary at all pressure above the triple point). Shown in figure is a combined P−T phase diagram for material A and B.
_E01_195_Q01.png)
If heat is added to solids A and B , each in a container that is open to the atmosphere :-
View SolutionEach phase of a material can exits only in certain regions of pressure and temperature . P−T phase diagrams, in which pressure is plotted versus temperature, show the regions corresponding to various phases and phase transformations . P−V diagrams, on the other hand , can be used to study pressure volume relationship at a constant temperature.
If the liquid and gaseous phases of a pure substances are heated together in a closed container, both the temperature and the vapor pressure will increase until a point is reached at which the two phases can no longer be distinguished from one another. The temperature and pressure at which this occurs are called the critical temperature and pressure. Exceeding either of these parameters, by itself ,will cause the gas/liguid phase transition to disappear. if the other variable is then changed as well, while the first variable is maintained above its critical point , a gradual transition will occur between the gaseous and liquid phases, with no clear boundary.(The liquid and solid phases, on the other hand , maintain a distinct boundary at all pressure above the triple point). Shown in figure is a combined P−T phase diagram for material A and B.
_E01_196_Q01.png)
Which is true about the substance in figure?
View Solution
Knowledge Check
When water is heated in a closed system, the vapor pressure increase slowly at first and then more rapidly. As the water reaches the boiling point of 100∘C, the vapor pressure reaches 1 atm, known as 1 standard atmosphere. Which of the following models best describes the increase in vapor pressure as water is heated to its boiling point?
ALinearBQuadraticCPolynomialDExponential
A thin - walled cylinder of mass (m), height (h) and cross- sectional area (A) is filled with a gas and floats on the surface of water. As a result of leakage from the lower part of the cylinder, the depth of its submergence has increased byΔh. Find the initial pressure p1 of the gas in the cylinder if the atmospheric pressure is p0 and the temperature remains constant.
View SolutionAt 70°C the vapor pressure of pure water is 31 kPa. Which of the following is most likely the vapor pressure of a 2.0 molal aq. glucose solution at 70°C?
View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
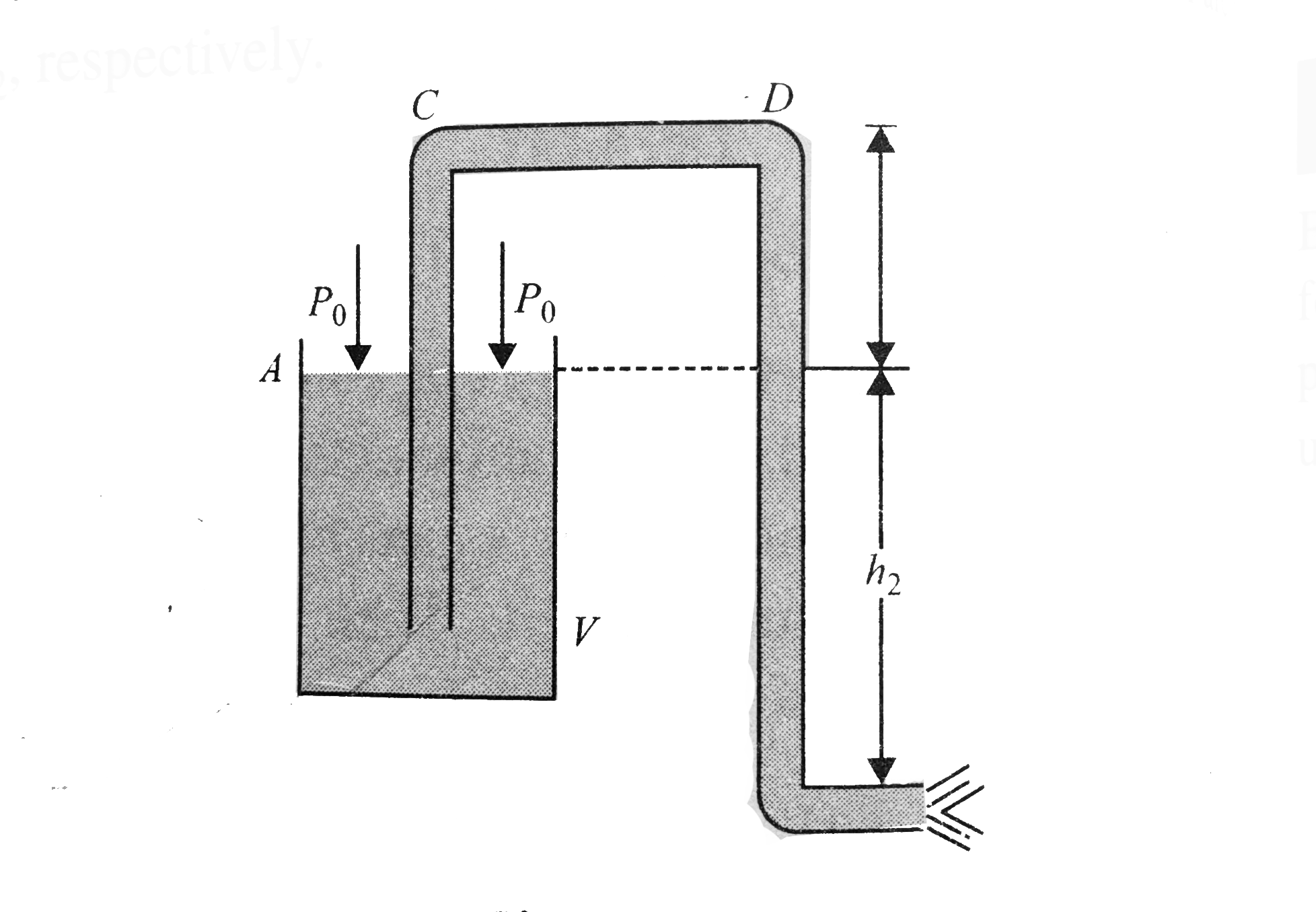
If h1=h2=3.0m, the maximum value of h1, for which the siphon will work will be
View SolutionA liquid having density 6000kg/m3 stands to a height of 4m in a sealed tank as shown in the figure. The tank contains compressed air at a gauge pressure of 3atm. The horizontal outlet pipe has a cross-sectional area of 6cm2 and 3cm2 at larger and smaller sections. Atmospheric pressure =1atm,g=10m/s21atm=105N/m2.

Assume that depth of water in the tank remains constant due to s very large base and air pressure above it remains constant. Based on the above information, answer the following questions.
The discharge rate from the outlet is
View SolutionFigure shows a large closed cylindrical tank containing water, Initially the air trapped above the water surface has a height h0and pressure 2p0 where p0is the atmospheric pressure. There is a hole in the wall of tank at a depth h1below the top from which water comes out. A long vertical tube is connected as shown. (a) Find the height h2 of the water in the long tube above the top initially. (b) Find the speed with which water comes out of hole.(c)Find the height of the water in the long tube above the top when the water stops coming out of the hole.

View SolutionIn a container of negligible heat capacity, 200gm ice at 0∘C and 100gm steam at 100∘C are added to 200gm of water that has temperature 55∘C. Assume no heat is lost to the surroundings and the pressure in the container is constant 1.0atm. (Latent heat of fusion of ice =80cal/gm, Latent heat of vaporization of water =540cal/gm, Specific heat capacity of ice =0.5cal/gm−K, Specific heat capacity of water =1cal/gm−K)
What is the final temperature of the system ?
View SolutionIn a container of negligible heat capacity, 200gm ice at 0∘C and 100gm steam at 100∘C are added to 200gm of water that has temperature 55∘C. Assume no heat is lost to the surrpundings and the pressure in the container is constant 1.0atm. (Latent heat of fusion of ice =80cal/gm, Latent heat of vaporization of water =540cal/gm, Specific heat capacity of ice =0.5cal/gm−K, Specific heat capacity of water =1cal/gm−K)
Amount of the steam left in the system, is equal to
View Solution
