An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area and weight 1kg. The length of the gas column in the vessel now taken into a spaceship revolving round the earth as satellite. The air pressure in the spaceship is maintained at 100kPa. Find the length of the gas column in the cylinder.
To solve the problem step-by-step, we will follow the reasoning provided in the video transcript and apply the principles of the kinetic theory of gases and the ideal gas law.
Step 1: Understand the Given Information
We have a cylindrical vessel with:
- Cross-sectional area A=10cm2=10×10−4m2=10−3m2
- Weight of the piston m=1kg
- Gravitational acceleration g=9.8m/s2
- Atmospheric pressure Patm=1×105Pa
- Pressure in the spaceship P2=100kPa=1×105Pa
Step 2: Calculate the Pressure Inside the Cylinder on Earth
When the gas is on Earth, the pressure inside the cylinder P1 can be calculated as:
P1=Patm+mgA
Substituting the values:
P1=1×105+1×9.810×10−4
Calculating the second term:
mgA=1×9.810×10−4=9.8×103Pa
Thus,
P1=1×105+9.8×103=109.8×103Pa
Step 3: Calculate the Volume of Gas on Earth
The volume V1 of the gas can be calculated using the formula:
V1=A×h
Given that the height h=0.20m:
V1=10−3×0.20=2×10−4m3
Step 4: Apply Boyle's Law for the Gas in the Spaceship
In the spaceship, the pressure is maintained at P2=1×105Pa. According to Boyle's Law:
P1V1=P2V2
Where V2=A×h (height of the gas column in the spaceship).
Step 5: Substitute the Known Values into Boyle's Law
Substituting the known values:
(109.8×103)×(2×10−4)=(1×105)×(h×10−3)
Calculating the left side:
(109.8×103)×(2×10−4)=21.96Pa
Now we have:
21.96=(1×105)×(h×10−3)
Step 6: Solve for Height h
Rearranging the equation to solve for h:
h=21.961×105×10−3=21.96100=0.2196m
Rounding off, we find:
h≈0.22m
Final Answer
The length of the gas column in the cylinder when taken into the spaceship is approximately 0.22m.
---
We have a cylindrical vessel with:
- Cross-sectional area A=10cm2=10×10−4m2=10−3m2
- Weight of the piston m=1kg
- Gravitational acceleration g=9.8m/s2
- Atmospheric pressure Patm=1×105Pa
- Pressure in the spaceship P2=100kPa=1×105Pa
When the gas is on Earth, the pressure inside the cylinder P1 can be calculated as:
P1=Patm+mgA
Substituting the values:
P1=1×105+1×9.810×10−4
Calculating the second term:
mgA=1×9.810×10−4=9.8×103Pa
Thus,
P1=1×105+9.8×103=109.8×103Pa
The volume V1 of the gas can be calculated using the formula:
V1=A×h
Given that the height h=0.20m:
V1=10−3×0.20=2×10−4m3
In the spaceship, the pressure is maintained at P2=1×105Pa. According to Boyle's Law:
P1V1=P2V2
Where V2=A×h (height of the gas column in the spaceship).
Substituting the known values:
(109.8×103)×(2×10−4)=(1×105)×(h×10−3)
Calculating the left side:
(109.8×103)×(2×10−4)=21.96Pa
Now we have:
21.96=(1×105)×(h×10−3)
Rearranging the equation to solve for h:
h=21.961×105×10−3=21.96100=0.2196m
Rounding off, we find:
h≈0.22m
The length of the gas column in the cylinder when taken into the spaceship is approximately 0.22m.
Topper's Solved these Questions
Similar Questions
An ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10cm2 and weight 1kg.The vessel itself is kept in a big chamber containing air at atmospheric pressure 100kPa. The length of the gas column is 20cm.if the chamber is now completely evacuated by an exhaust pump, what will be the length of the gas column? Assume the tempaerature to remain constant throughout the process.
 View Solution
View SolutionA satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
View SolutionA satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
View SolutionA diatomic gas is enclosed in a vessel fitted with massless movable piston. Area of cross section of vessel is 1m2. Initial height of the piston is 1m (see the figure). The initial temperature of the gas is 300K. The temperature of the gas is increased to 400K, keeping pressure constant, calculate the new height of the piston. The piston is brought to its initial position with no heat exchange. Calculate the final temperature of the gas. You can leave answer in fraction.
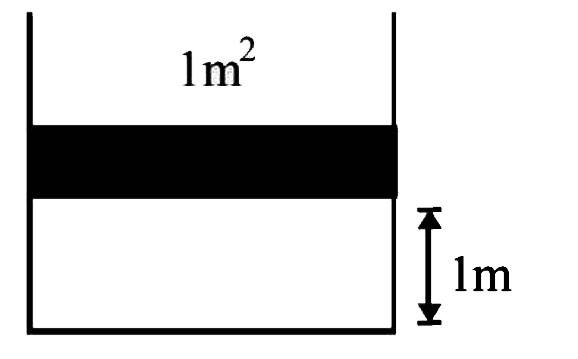 View Solution
View SolutionAn ideal gas is enclosed in a cylinder fitted with a frictionless piston. The piston is connected with a light rod to one plate of capacitor whose other plate is fixed as shown. Initially volume of the gas inside the cylinder is V0 Atmospheric pressure is P0 separation between the plates is L, area of the piston as well as of the capacitor plates is A and emf of battery is ε . A heater supplies heat to the gas so that pressure of the gas is given as P=P0−nε0ε2L2 when piston is displaced by a distance L2 . Find value of n.
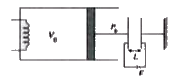 View Solution
View SolutionA gas is enclosed in a cylindrical vessel fitted with a frictionless piston.the gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10cm. Find the increase in the internal energy of the gas, the area of cross section of the cylinder=4cm2 and the atmospheric pressure =100kPa.
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4×10−3m2. The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m. The temperature of the gas increases by 50K. Calculate the spring constant and the heat supplied by the heater. Patm=1×105N/m2R=8.314J/mol−K
View SolutionTwo cylindrical vessels fitted with pistons A and B of area of cross section 8cm2 and 320cm2 respectively. Are joined at their bottom by a tube and they are completely filled with water. When a mass of 4 kg is placed on piston A, find : (i) the pressure on piston A, (ii) the pressure on piston B and (iii) the thrust on piston B.
View SolutionA closed cubical box is made of perfectly insulating material and the only way for heat to enter or leave the box is through two solid cylindrical metal plugs, each of cross sectional area 12cm2 and length 8cm fixed in the opposite walls of the box. The outer surface of one plug is kept at a temperature of 100∘C . while the outer surface of the plug is maintained at a temperature of 4∘C . The thermal conductivity of the material of the plug is 2.0Wm−1C−1 . A source of energy generating 13W is enclosed inside the box. Find the equilibrium temperature of the inner surface of the box assuming that it is the same at all points on the inner surface.
View Solution
A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is P0 and temperature is T0, atmospheric pressure is also P0. Now the temperature of the gas is increased to 2T0, the tension in the wire will beView Solution

