A faulty barometer contains certains amount of air and saturated water vapour . It reads 74.0cm when the atmospheric pressure is 76.0cm of mercury and reads 72.10cm when the atmospheric pressure is 74.0cm of mercury.Saturation vapour pressure at air temperature =1.0cm of mercury. Find the length of the baromerer tube above the mercury level in the reservoir.
To solve the problem, we need to determine the length of the barometer tube above the mercury level in the reservoir. We will use the information provided about the readings of the faulty barometer and the atmospheric pressures.
1. Understanding the Problem:
- We have a faulty barometer that reads different heights of mercury (74.0 cm and 72.1 cm) at different atmospheric pressures (76.0 cm and 74.0 cm of mercury).
- The saturation vapor pressure at the air temperature is given as 1.0 cm of mercury.
2. Define Variables:
- Let h be the length of the barometer tube above the mercury level in the reservoir.
- Let x be the height of the air column above the mercury level.
3. Calculate the Pressure of the Gas:
- In the first case, when the atmospheric pressure is 76.0 cmHg and the barometer reads 74.0 cm:
P1=76.0−74.0=2.0cmHg
The pressure of the gas (considering the saturation vapor pressure) is:
Pgas1=P1−PSVP=2.0−1.0=1.0cmHg
- In the second case, when the atmospheric pressure is 74.0 cmHg and the barometer reads 72.1 cm:
P2=74.0−72.1=1.9cmHg
The pressure of the gas is:
Pgas2=P2−PSVP=1.9−1.0=0.9cmHg
4. Calculate the Volume of the Air Column:
- The volume of the air column in the first case is:
V1=A(h−74.0)
- The volume of the air column in the second case is:
V2=A(h−72.1)
Here, A is the cross-sectional area of the barometer tube.
5. Apply Boyle's Law:
- Since the temperature is constant, we can apply Boyle's Law:
Pgas1V1=Pgas2V2
Substituting the values we have:
1.0⋅A(h−74.0)=0.9⋅A(h−72.1)
We can cancel A (assuming it is non-zero):
1.0(h−74.0)=0.9(h−72.1)
6. Solve for h:
- Expanding both sides:
h−74.0=0.9h−64.89
- Rearranging gives:
h−0.9h=74.0−64.89
0.1h=9.11
h=9.110.1=91.1cm
Final Answer:
The length of the barometer tube above the mercury level in the reservoir is 91.1 cm.
- We have a faulty barometer that reads different heights of mercury (74.0 cm and 72.1 cm) at different atmospheric pressures (76.0 cm and 74.0 cm of mercury).
- The saturation vapor pressure at the air temperature is given as 1.0 cm of mercury.
- Let h be the length of the barometer tube above the mercury level in the reservoir.
- Let x be the height of the air column above the mercury level.
- In the first case, when the atmospheric pressure is 76.0 cmHg and the barometer reads 74.0 cm:
P1=76.0−74.0=2.0cmHg
The pressure of the gas (considering the saturation vapor pressure) is:
Pgas1=P1−PSVP=2.0−1.0=1.0cmHg
P2=74.0−72.1=1.9cmHg
The pressure of the gas is:
Pgas2=P2−PSVP=1.9−1.0=0.9cmHg
- The volume of the air column in the first case is:
V1=A(h−74.0)
- The volume of the air column in the second case is:
V2=A(h−72.1)
Here, A is the cross-sectional area of the barometer tube.
- Since the temperature is constant, we can apply Boyle's Law:
Pgas1V1=Pgas2V2
Substituting the values we have:
1.0⋅A(h−74.0)=0.9⋅A(h−72.1)
We can cancel A (assuming it is non-zero):
1.0(h−74.0)=0.9(h−72.1)
- Expanding both sides:
h−74.0=0.9h−64.89
- Rearranging gives:
h−0.9h=74.0−64.89
0.1h=9.11
h=9.110.1=91.1cm
The length of the barometer tube above the mercury level in the reservoir is 91.1 cm.
Topper's Solved these Questions
Similar Questions
The atmospheric pressure on a hill is 68 cm of mercury. What do you understand from the statement?
View SolutionThe length of a faulty barometer is 90 cm and there is a little air above the mercury. When the atmospheric pressure is 76cm of Hg it reads 74.8 cm. What will be the true atmospheric pressure if the reading on the barometer is 74.3cm ?
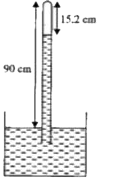
View Solution
Knowledge Check
A manometer reads the pressure of a gas in an enclosure as shown in the figure. The absolute and gauge pressure of the gas in cm of mercury is (take atmospheric pressure =76 cm of mercury)
A76,20B20,76C96,20D20,96
At sea level, the atmospheric pressure is 76 cm of Hg. If air pressure falls by 10 mm of Hg per 120 m of ascent, what is the height of a hill where the barometer reads 70 cm Hg.
View SolutionA barometer correctly reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric temperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionA jar contains a gas and a few drops of water at absolute temperture T_(1). The pressure in the jar is 830mmof mercuryand 25mmof mercury. The temperature of the jar is reduced by 1%. The saturation vapour pressures of water at the two temperatures are 30mm of murcury and 25mm of mercury. Calculate the new pressue in the jar.
View SolutionOne litre of air at 76 cm of mercury is compressed to a pressure of 152 cm of mercury under isothermal conditions. What is the new volume ?
View SolutionIf water be used to construct a barometer, what would be the height of water column at a standard atmospheric presure (76cm of mercury)?
View SolutionA manometer is connected to a gas containing bulb The open arm reads 43.7cm where as the arm connected to the bulb reads 15.6cm If the barometric pressure is 743mm mercury What is the pressure of gas in bar ? .
View SolutionAt sea level, the atmospheric pressure is 76 cm of Hg. If air pressure falls by 10 mm of Hg per 120 m of ascent, what is the height of a hill where the barometer reads 70 cm Hg. State the assumption made by you. .
View Solution
