Two masses M1andM2 are connected by a light rod and the system is slipping down a rough incline of angle θ with the horizontal. The friction coefficient at both the contacts is μ. Find the acceleration of the system, and the force by the rod on one of the blocks.
To solve the problem of two masses M1 and M2 connected by a light rod slipping down a rough incline, we will follow these steps:
Step 1: Draw the Free Body Diagram
Draw the incline and label the angle θ. Mark the two masses M1 and M2 on the incline. Identify the forces acting on each mass: the gravitational force, the normal force, and the frictional force.
Step 2: Identify Forces Acting on Each Mass
For mass M1:
- Gravitational force down the incline: Fg1=M1gsinθ
- Normal force: N1=M1gcosθ
- Frictional force (acting up the incline): Ff1=μN1=μM1gcosθ
For mass M2:
- Gravitational force down the incline: Fg2=M2gsinθ
- Normal force: N2=M2gcosθ
- Frictional force (acting up the incline): Ff2=μN2=μM2gcosθ
Step 3: Write the Equations of Motion
For mass M1:
M1gsinθ−μM1gcosθ=M1a
This simplifies to:
gsinθ−μgcosθ=a
For mass M2:
M2gsinθ−μM2gcosθ=M2a
This simplifies to:
gsinθ−μgcosθ=a
Step 4: Find the Acceleration of the System
From the equations derived, we can see that both masses have the same acceleration:
a=gsinθ−μgcosθ
Step 5: Analyze the Force by the Rod
Since both masses M1 and M2 are accelerating at the same rate, the rod does not exert any force on either mass. Thus, the force by the rod on one of the blocks is:
Frod=0
Final Answers
1. The acceleration of the system is:
a=gsinθ−μgcosθ
2. The force by the rod on one of the blocks is:
Frod=0
---
Draw the incline and label the angle θ. Mark the two masses M1 and M2 on the incline. Identify the forces acting on each mass: the gravitational force, the normal force, and the frictional force.
For mass M1:
- Gravitational force down the incline: Fg1=M1gsinθ
- Normal force: N1=M1gcosθ
- Frictional force (acting up the incline): Ff1=μN1=μM1gcosθ
- Gravitational force down the incline: Fg2=M2gsinθ
- Normal force: N2=M2gcosθ
- Frictional force (acting up the incline): Ff2=μN2=μM2gcosθ
For mass M1:
M1gsinθ−μM1gcosθ=M1a
This simplifies to:
gsinθ−μgcosθ=a
M2gsinθ−μM2gcosθ=M2a
This simplifies to:
gsinθ−μgcosθ=a
From the equations derived, we can see that both masses have the same acceleration:
a=gsinθ−μgcosθ
Since both masses M1 and M2 are accelerating at the same rate, the rod does not exert any force on either mass. Thus, the force by the rod on one of the blocks is:
Frod=0
1. The acceleration of the system is:
a=gsinθ−μgcosθ
2. The force by the rod on one of the blocks is:
Frod=0
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer11videos
FRICTION
- BOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Objective -25videos
FRICTION
- BOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions90videos
FLUID MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers18videos
GRAVITATION
Similar Questions
A block slides down an inclined plane that makes an angle θ with the horizontal. If the coefficient of kinetic friction is μ, find the acceleration of the block.
View SolutionA block of mass m is placed on a rough plane inclined at an angle θ with the horizontal. The coefficient of friction between the block and inclined plane is μ . Ifθ<tan−1(μ) , then net contact force exerted by the plane on the block is :
View SolutionA block of mass m slides down an inclined plane which makes an angle θ with the horizontal. The coefficient of friction between the block and the plane is μ. The force exerted by the block on the plane is
View SolutionA block of mass m is placed at rest on an inclination θ to the horizontal. If the coefficient of friction between the block and the plane is μ, then the total force the inclined plane exerts on the block is
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionTwo bodies of masses m1andm2 are connected by a light string going over a smooth lilght pulley at the end of an incline. The mass1 lies on the incline m2 hangs vertically. The system is t rest. Find the angle of the incline and the fore exerted by the incline on the body of mass m_1.
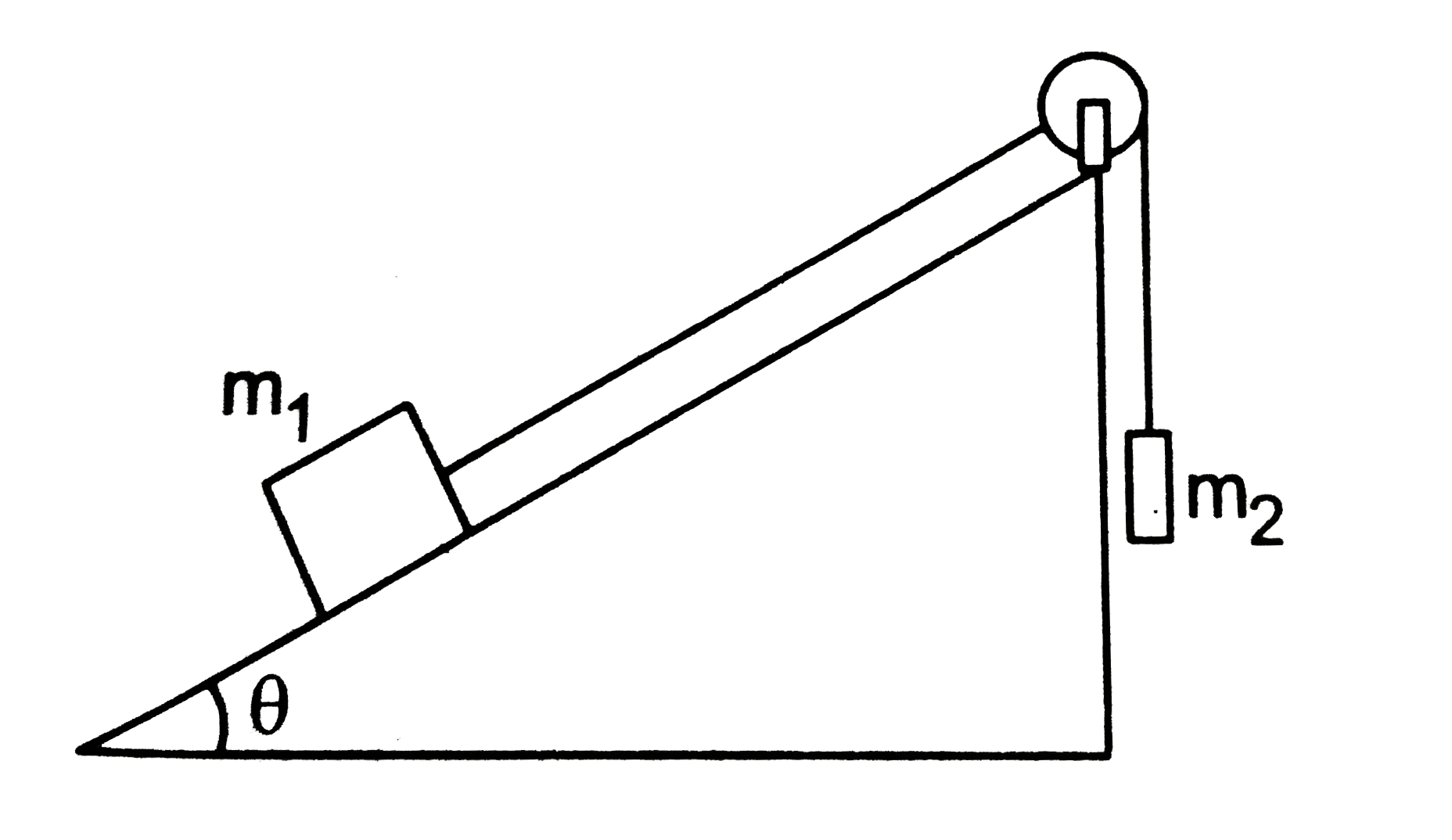 View Solution
View SolutionTwo small spheres of masses m1 and m2 are connected by a light right rod.The system is placed between a rought floor and smooth verticle wall as shown in Fig. The co-efficent of friction between the floor and the sphere of mass m2 isμ .Find the minimum value of θ so that the system of masses does not slip
 View Solution
View SolutionTwo blocks of masses m1=1kgandm2=2kg are connected by a string and side down a plane inclined at an angle θ=45∘ with the horizontal. The coefficient of sliding friction between m1 and plane is μ1=0.4, and that between m2 and plane is μ2=0.2. Calculate the common acceleration of the two blocks and the tension in the string.
 View Solution
View SolutionA block of mass m sides down an inclined right angled trough .If the coefficient of friction between block and the trough is μk acceleration of the block down the plane is
 View Solution
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View Solution

