Equal torques asct on the discs A and B of theh previous problem, initially both being at rest. At a later instant, theliear speeds of a point on therim of a A another potin on the rim of B are VAandVB respectively. We have
VA<VB
VA=VB
VA<VB
the relation depends on the tactual magnitude of the torques
The correct Answer is:A
To solve the problem, we need to establish the relationship between the linear speeds VA and VB of points on the rims of discs A and B, respectively. Here's a step-by-step solution:
Step 1: Understand the Given Information
We have two discs, A and B:
- Disc A has a radius r and moment of inertia IA.
- Disc B has a radius 4r and moment of inertia IB.
- Equal torques τ are applied to both discs, and they start from rest.
Step 2: Relate the Moments of Inertia
From the previous problem, we know that:
IB=64IA
This is because the moment of inertia for a disc is proportional to the square of its radius, and since 4r is four times the radius of r, the moment of inertia increases by a factor of 42=16. However, since the thickness is also considered, the total factor becomes 16×4=64.
Step 3: Calculate Angular Acceleration
Using the relation for torque:
τ=IAαAandτ=IBαB
We can express the angular accelerations αA and αB:
αA=τIAandαB=τIB
Substituting IB=64IA:
αB=τ64IA=164τIA=164αA
Step 4: Calculate Angular Velocities
Since both discs start from rest, we can use the equation for angular velocity:
ωA=αAtandωB=αBt
Substituting for αB:
ωB=(164αA)t=164ωA
Step 5: Relate Linear Velocities
The linear velocities at the rim of the discs are given by:
VA=rωAandVB=4rωB
Substituting ωB:
VB=4r(164ωA)=4r64ωA=r16ωA
Step 6: Substitute for VA
Now substituting for VA:
VA=rωA
Thus, we can express the relationship between VA and VB:
VB=r16VAr=116VA
Step 7: Conclusion
From the above relationship, we conclude:
VA=16VB
This means that the linear speed of point A is greater than that of point B, confirming that:
VA>VB
We have two discs, A and B:
- Disc A has a radius r and moment of inertia IA.
- Disc B has a radius 4r and moment of inertia IB.
- Equal torques τ are applied to both discs, and they start from rest.
From the previous problem, we know that:
IB=64IA
This is because the moment of inertia for a disc is proportional to the square of its radius, and since 4r is four times the radius of r, the moment of inertia increases by a factor of 42=16. However, since the thickness is also considered, the total factor becomes 16×4=64.
Using the relation for torque:
τ=IAαAandτ=IBαB
We can express the angular accelerations αA and αB:
αA=τIAandαB=τIB
Substituting IB=64IA:
αB=τ64IA=164τIA=164αA
Since both discs start from rest, we can use the equation for angular velocity:
ωA=αAtandωB=αBt
Substituting for αB:
ωB=(164αA)t=164ωA
The linear velocities at the rim of the discs are given by:
VA=rωAandVB=4rωB
Substituting ωB:
VB=4r(164ωA)=4r64ωA=r16ωA
Now substituting for VA:
VA=rωA
Thus, we can express the relationship between VA and VB:
VB=r16VAr=116VA
From the above relationship, we conclude:
VA=16VB
This means that the linear speed of point A is greater than that of point B, confirming that:
VA>VB
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples
29 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
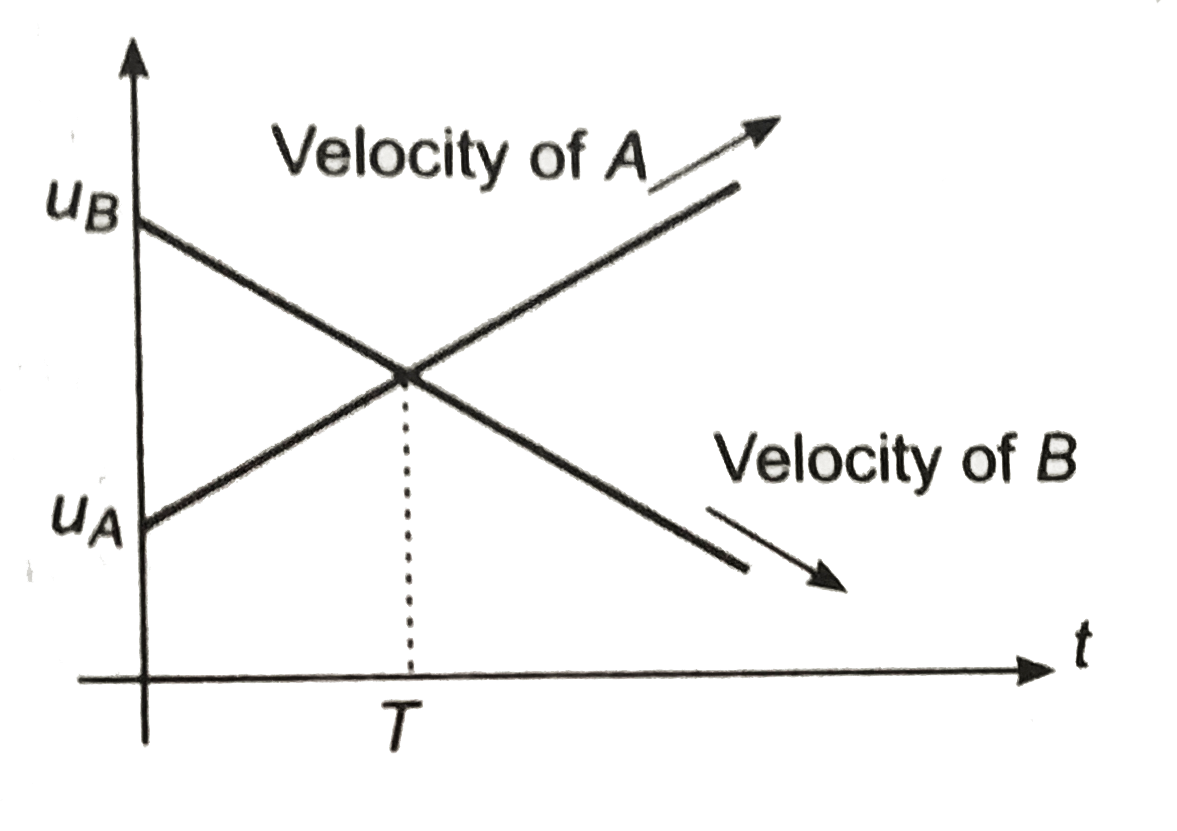
A situation is shown in which two objects A and B start their motion from same point in same direction. The graph of their velocities against time is drawn. uAanduB are the initial velocities of A and B respectively. T is the time at which their velocities become equal after start of motion. You cannot use the data of one question while solving another question of the same set. So all the questions are independent of each other.
6. Let vAandvB be the velocities of the particles A and B respectively at the moment A and B meet after start of the motion. If uA=5ms−1anduB=15ms−1, then the magnitude of the difference of velocities vAandvB is
View SolutionConsider the elastic collision f two bodies A and B of equal mass. Initially B is at rest and A moves with velocity v. After the collision -
View Solution
Knowledge Check
Two particles A and B, initially at rest, moves towards each other under a mutual force of attraction. At the instant when the speed of A is v and the speed of B is 2 v, the speed of centre of mass is
AzeroBvC1.5 vD3 vTwo particles A and B intiallly at rest, move towards each other under a mutual force of attraction. AT the instant when the speed of A is v and the speed of B is 2 v, the speed of the centre of mass of the system is
AzeroBvC1.5 vD3 v
A uniform electric field E0 exists in a region at angle 45∘ with the x - axis. There are two point A(a,0)andB(0,b) having potential VAandVB, respectively, then
 .
.
View SolutionTwo particles A and B with particle A having mass m, are moving towards each other under their mutual force of attraction. If their speeds at certain instant are v and 2v respectively, then find the K.E. of the system.
View SolutionTwo particles A and B of masses mA and mB respectively and having the same charge are moving ina plane. A uniform magnetic field exists perependicular to this plane. The speeds of the particles are vA and vB respectively and the trajectories are as shown in the figure. Then,

View SolutionIn the given circuit diagram, both capacitors are initially uncharged. The capacitance C1=2μFandC2=4μF, emf of battery A and B are 2V and 4V respectively.


View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration a1anda2 respectively. Show that v=√a1a2t.
View SolutionIn a car race, car A takes a time t less than car B at the finish and passes the finishing point with speed v more than that of the car B. Assuming that both the cars start from rest and travel with constant acceleration a1anda2 respectively. Show that v=√a1a2t.
View Solution
