A circular disc A of radius r is made from an iron plate of thickness t and another circular disc B of radius 4r is made from an iron plate of thickness t/4. The relation between the moments of inertia IAandIB is
IA>IB
IA=IB
IA<IB
depends on the actual values of t and r
The correct Answer is:C
To find the relation between the moments of inertia IA and IB for the two circular discs, we will follow these steps:
Step 1: Calculate the Mass of Disc A
The mass mA of disc A can be calculated using the formula:
mA=Density×Volume
The volume VA of disc A is given by:
VA=Area×Thickness=πr2×t
Thus, the mass of disc A is:
mA=ρ×VA=ρ×πr2t
Step 2: Calculate the Moment of Inertia of Disc A
The moment of inertia IA for a circular disc is given by:
IA=12mAr2
Substituting the expression for mA:
IA=12(ρπr2t)r2=12ρπtr4
Step 3: Calculate the Mass of Disc B
For disc B, the radius is 4r and the thickness is t4. The volume VB of disc B is:
VB=π(4r)2×t4=π×16r2×t4=4πr2t
Thus, the mass of disc B is:
mB=ρ×VB=ρ×4πr2t
Step 4: Calculate the Moment of Inertia of Disc B
The moment of inertia IB for disc B is:
IB=12mB(4r)2
Substituting the expression for mB:
IB=12(ρ×4πr2t)(16r2)=12×4×16ρπr2t×r2=32ρπtr4
Step 5: Compare the Moments of Inertia
Now we have:
IA=12ρπtr4
IB=32ρπtr4
To compare IA and IB:
IB=64IA
Thus, we find that:
IA<IB
Conclusion
The relation between the moments of inertia IA and IB is:
IA<IB
The mass mA of disc A can be calculated using the formula:
mA=Density×Volume
The volume VA of disc A is given by:
VA=Area×Thickness=πr2×t
Thus, the mass of disc A is:
mA=ρ×VA=ρ×πr2t
The moment of inertia IA for a circular disc is given by:
IA=12mAr2
Substituting the expression for mA:
IA=12(ρπr2t)r2=12ρπtr4
For disc B, the radius is 4r and the thickness is t4. The volume VB of disc B is:
VB=π(4r)2×t4=π×16r2×t4=4πr2t
Thus, the mass of disc B is:
mB=ρ×VB=ρ×4πr2t
The moment of inertia IB for disc B is:
IB=12mB(4r)2
Substituting the expression for mB:
IB=12(ρ×4πr2t)(16r2)=12×4×16ρπr2t×r2=32ρπtr4
Now we have:
IA=12ρπtr4
IB=32ρπtr4
IB=64IA
IA<IB
The relation between the moments of inertia IA and IB is:
IA<IB
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples
29 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A uniform circular disc A of radius r is made from A copper plate of thickness t and another uniform circular disc B of radius 2r is made from a copper plate of thickness t/2. The relation between the moments of inertia IAandIB is?
View SolutionA circular disc X of radius R is made from an iron of thickness t, and another disc Y of radius 4R is made from an iron plate of thickness t/4. Then the relation between the moment of mertia Ix and IY is :
View SolutionTwo circular discs are of same thickness. The diameter of A is twice that of B. The moment of inertia of A as compared to that of B is
View SolutionIf two circular discs A and B are of same mass but of radii r and 2r respectively, then the moment of inertia of A is
View SolutionA circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of new disc is αR from the center of the bigger disc. The value of α is
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionA concentric hole of radius R/2 is cut from a thin circular plate of mass M and radius R. The moment of inertia of the remaining plate about its axis will be
View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
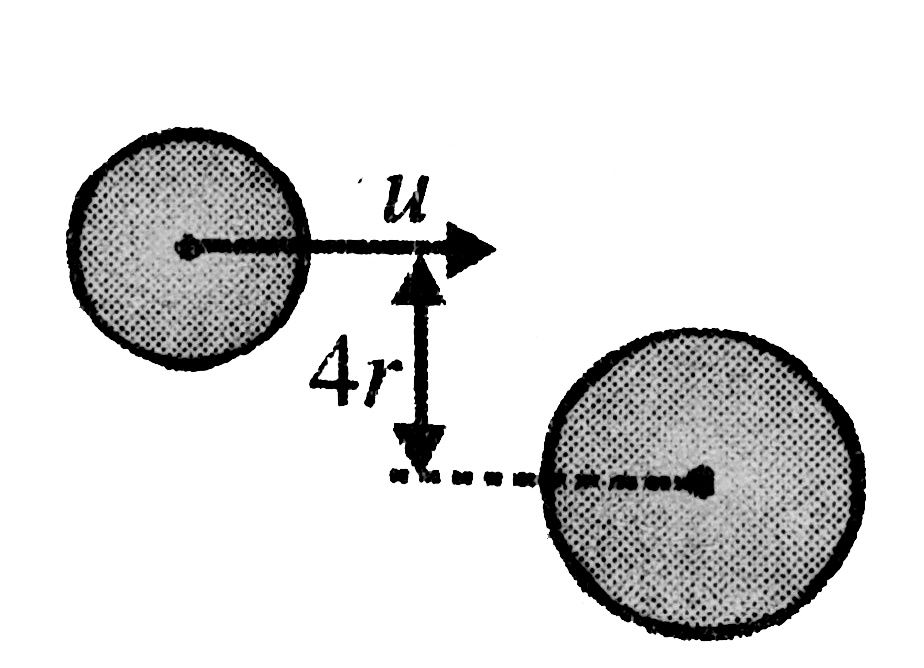 What is the final velocity of the heavier disc?
What is the final velocity of the heavier disc?
View SolutionA circular disc of mass '2m' and radius '3r' is resting on a flat frictionless surface. Another circular disc of mass m and radius '2r', moving with a velocity 'u'. hits the first disc as shown in the figure. The collision is elastic.
What is the magnitude of normal component of final velocity of the smaller disc'?
View Solution
