A body having its centre of mass at the origin has three of its particles at (a,0,0),(0,a,0),(0,0,a). The moments of inertia of the body about the X and Y axes are 0.20 kg −m2 each. The moment of inertia about the Z-axis
is 0.20 kg−m2
is 0.40 kg−m2
is 0.20√2 kg−m2
cannot be deduced with this information.
The correct Answer is:D
To find the moment of inertia of the body about the Z-axis, we can follow these steps:
Step 1: Identify the particles and their positions
We have three particles located at:
- Particle 1: (a,0,0)
- Particle 2: (0,a,0)
- Particle 3: (0,0,a)
Step 2: Understand the moment of inertia formula
The moment of inertia I about an axis for a system of particles is given by the formula:
I=∑mir2i
where mi is the mass of the particle and ri is the perpendicular distance from the axis of rotation to the particle.
Step 3: Calculate the moment of inertia about the X-axis
For the X-axis:
- Particle 1 contributes 0 because it lies on the X-axis.
- Particle 2 contributes m2a2 (distance from the X-axis is a).
- Particle 3 contributes m3a2 (distance from the X-axis is a).
Thus, the moment of inertia about the X-axis is:
Ix=0+m2a2+m3a2=(m2+m3)a2
Given Ix=0.2kg m2, we have:
(m2+m3)a2=0.2(Equation 1)
Step 4: Calculate the moment of inertia about the Y-axis
For the Y-axis:
- Particle 1 contributes m1a2 (distance from the Y-axis is a).
- Particle 2 contributes 0 because it lies on the Y-axis.
- Particle 3 contributes m3a2 (distance from the Y-axis is a).
Thus, the moment of inertia about the Y-axis is:
Iy=m1a2+0+m3a2=(m1+m3)a2
Given Iy=0.2kg m2, we have:
(m1+m3)a2=0.2(Equation 2)
Step 5: Calculate the moment of inertia about the Z-axis
For the Z-axis:
- Particle 1 contributes m1a2 (distance from the Z-axis is a).
- Particle 2 contributes m2a2 (distance from the Z-axis is a).
- Particle 3 contributes 0 because it lies on the Z-axis.
Thus, the moment of inertia about the Z-axis is:
Iz=m1a2+m2a2+0=(m1+m2)a2
Step 6: Solve for Iz
To find Iz, we need to express m1+m2 in terms of known quantities. From Equations 1 and 2, we can express:
- m2+m3=0.2a2
- m1+m3=0.2a2
However, we have two equations with three unknowns, which means we cannot uniquely determine m1,m2, and m3 without additional information. Thus, we cannot deduce Iz with the information given.
Conclusion
The moment of inertia about the Z-axis cannot be determined with the information provided.
We have three particles located at:
- Particle 1: (a,0,0)
- Particle 2: (0,a,0)
- Particle 3: (0,0,a)
The moment of inertia I about an axis for a system of particles is given by the formula:
I=∑mir2i
where mi is the mass of the particle and ri is the perpendicular distance from the axis of rotation to the particle.
For the X-axis:
- Particle 1 contributes 0 because it lies on the X-axis.
- Particle 2 contributes m2a2 (distance from the X-axis is a).
- Particle 3 contributes m3a2 (distance from the X-axis is a).
Ix=0+m2a2+m3a2=(m2+m3)a2
Given Ix=0.2kg m2, we have:
(m2+m3)a2=0.2(Equation 1)
For the Y-axis:
- Particle 1 contributes m1a2 (distance from the Y-axis is a).
- Particle 2 contributes 0 because it lies on the Y-axis.
- Particle 3 contributes m3a2 (distance from the Y-axis is a).
Iy=m1a2+0+m3a2=(m1+m3)a2
Given Iy=0.2kg m2, we have:
(m1+m3)a2=0.2(Equation 2)
For the Z-axis:
- Particle 1 contributes m1a2 (distance from the Z-axis is a).
- Particle 2 contributes m2a2 (distance from the Z-axis is a).
- Particle 3 contributes 0 because it lies on the Z-axis.
Iz=m1a2+m2a2+0=(m1+m2)a2
To find Iz, we need to express m1+m2 in terms of known quantities. From Equations 1 and 2, we can express:
- m2+m3=0.2a2
- m1+m3=0.2a2
The moment of inertia about the Z-axis cannot be determined with the information provided.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - worked out Examples
29 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A particle of mass 1 kg is kept at (1m,1m,1m). The moment of inertia of this particle about Z-axis would be
View SolutionA mass of 1 kg is placed at (1m, 2m, 0). Another mass of 2 kg is placed at (3m, 3m, 0). Find the moment of inertial of both the masses about z-axis
View SolutionA wheel comprises a ring of radius R and mass M and three spokes of mass m each. The moment of inertia of the wheel about its axis is

View SolutionA symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
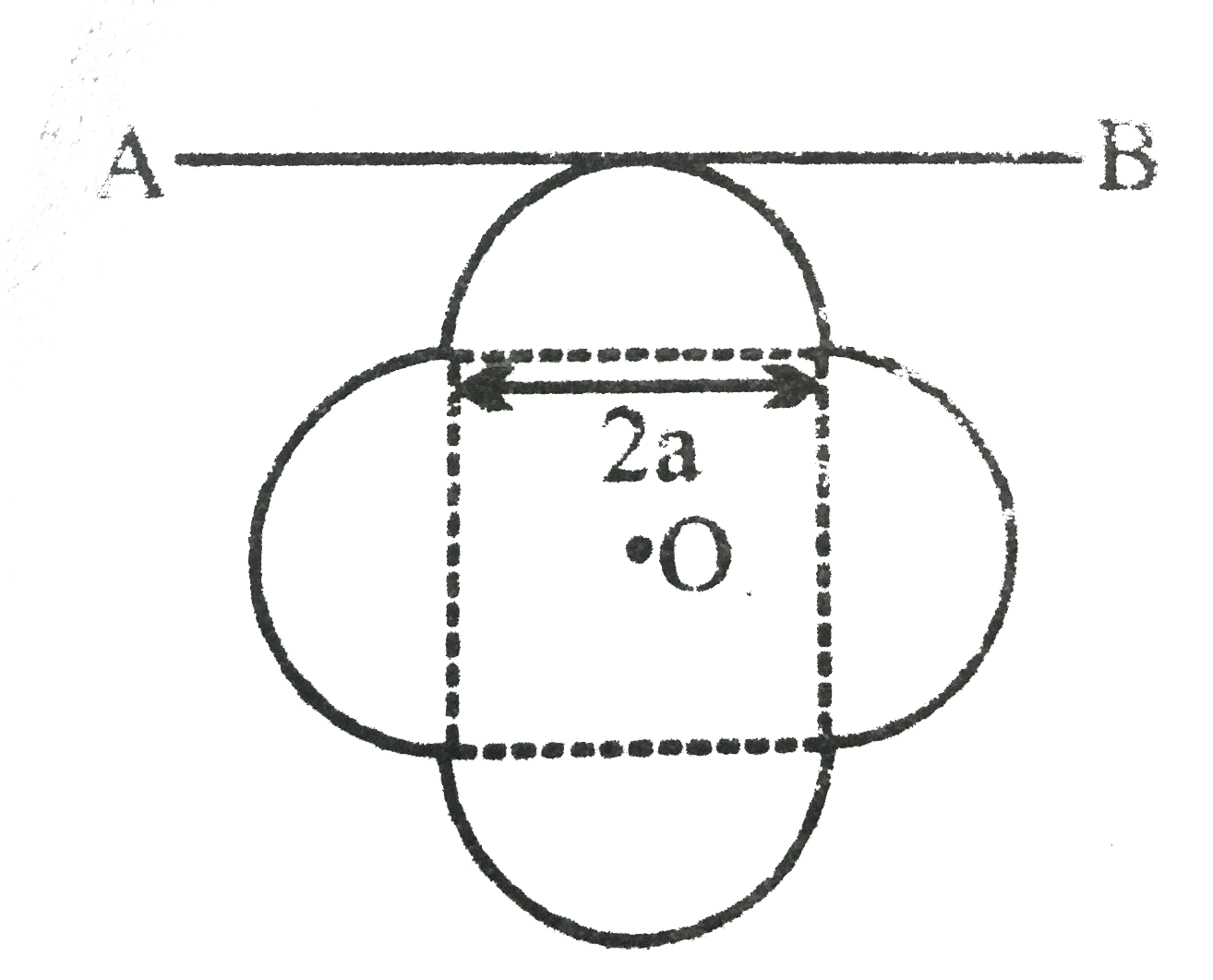 .
.
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionThe axis X and Z in the plane of a disc are mutually perpendicular and Y-axis is perpendicular to the plane of the disc. If the moment of inertia of the body about X and Y axes is respectively 30 kg m2 and 40 kg m2 then M.I. about Z-axis in kg m2 will be:
View SolutionFour identical rods, each of mass m and length l, make a square frame in the xy plane as shown in Fig.
a. Calculate its moment of inertia about the x-and y-axes.
b. Also, calculate its moment of inertia about the z-axis.

View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)
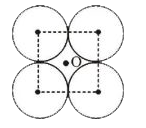
View SolutionFour solid spheres, each of mass (m) and diameter (d) are stuck together such that the lines joining the centres form a square of side length (d). The ratio of I0 & IA , where I0 is the moment of inertia of the system about an axis through the centre of the square and IA is moment of inertia of the system about the centre of any one of the spheres, is equal to (both axes are perpendicular to plane of paper)

View SolutionThe moment of inertia of a cube of mass M and edge length a about an axis passing through one of its edge is
View Solution
