A wheel of radius 20 cm is pushed ot move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolutionabout the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
along the velocity of the wheel
opposite to the velocity o the wheel
perpendicular to the velocity of the wheel
zero
The correct Answer is:A
To solve the problem, we need to analyze the motion of the wheel and the forces acting on it. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Given Information
- The radius of the wheel (R) = 20 cm = 0.2 m
- The distance traveled by the wheel in one complete revolution = 60 cm = 0.6 m
- The circumference of the wheel (C) = 2πR = 2π(0.2 m) = 0.4π m ≈ 0.628 m
Step 2: Compare the Distance Traveled with the Circumference
The distance traveled (0.6 m) is less than the circumference of the wheel (approximately 0.628 m). This indicates that the wheel is slipping as it rolls.
Step 3: Analyze the Motion
Since the wheel is rolling on a rough surface and the distance traveled is less than the circumference, it suggests that the translational speed of the wheel (Vt) is less than the rotational speed (Vr) at the point of contact.
Step 4: Determine the Direction of Friction
The frictional force acts to oppose the relative motion between the wheel and the surface. Since the wheel is slipping, the frictional force will act in the direction of the translational motion (the direction the wheel is rolling).
Step 5: Conclude the Direction of Frictional Force
Since the translational velocity (Vt) is less than the rotational velocity (Vr), the frictional force must act in the direction of Vt. Therefore, the frictional force is along the direction of the wheel's movement.
Step 6: Identify the Correct Option
From the options provided, the correct option states that the frictional force acting on the wheel is along the velocity of the wheel.
Final Answer
The frictional force acting on the wheel by the surface is directed along the velocity of the wheel.
---
- The radius of the wheel (R) = 20 cm = 0.2 m
- The distance traveled by the wheel in one complete revolution = 60 cm = 0.6 m
- The circumference of the wheel (C) = 2πR = 2π(0.2 m) = 0.4π m ≈ 0.628 m
The distance traveled (0.6 m) is less than the circumference of the wheel (approximately 0.628 m). This indicates that the wheel is slipping as it rolls.
Since the wheel is rolling on a rough surface and the distance traveled is less than the circumference, it suggests that the translational speed of the wheel (Vt) is less than the rotational speed (Vr) at the point of contact.
The frictional force acts to oppose the relative motion between the wheel and the surface. Since the wheel is slipping, the frictional force will act in the direction of the translational motion (the direction the wheel is rolling).
Since the translational velocity (Vt) is less than the rotational velocity (Vr), the frictional force must act in the direction of Vt. Therefore, the frictional force is along the direction of the wheel's movement.
From the options provided, the correct option states that the frictional force acting on the wheel is along the velocity of the wheel.
The frictional force acting on the wheel by the surface is directed along the velocity of the wheel.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -2
Explore 14 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercises
Explore 86 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:worked out Examples
Explore 29 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
Similar Questions
If a body has kinetic energy. T, moving on a rough horizontal surface stops at distance y. The frictional force exerted on the body is
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
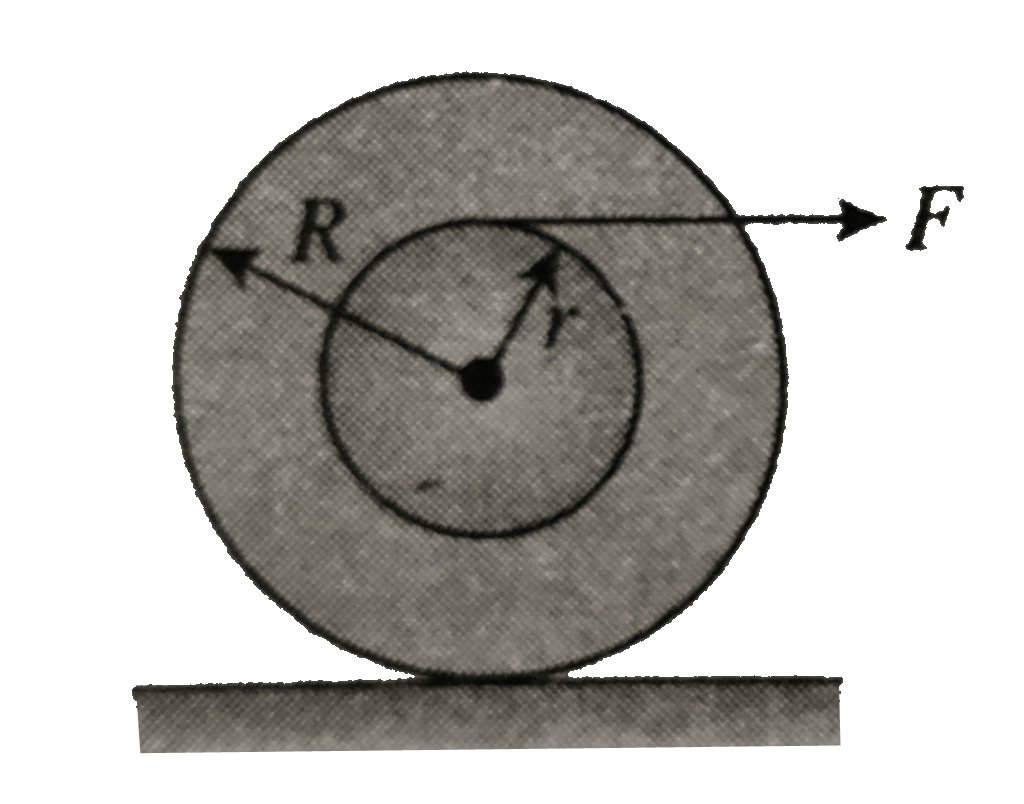
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

View SolutionA block of mass 5kg rests on a rough horizontal surface. It is found that a force of 10N is required to make the block just move However , once the motion begains, a force of only 8N is enough to maintain the motion find the coefficient of kinetic and static friction between the block and the horizontal surface

View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 200 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 5.00 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
View SolutionA uniform hollow sphere of mass 400 g rolls without slipping on a plane horizontal surface with its centre moving at a speed of 10 cm/s. Its kinetic energy is:
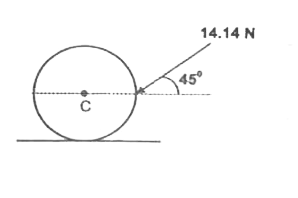
View SolutionA uniform sphere of mass 20kg and radius 10cm is placed on a rough horizontal surface . The coefficient of friction between the sphere and the surface is 0.5.If a force of magnitude 14.14 N is applied on the sphere at an angle of 45∘ with horizontal as shown in the figure, calculate
(a) frictional force
(b) acceleration of the sphere
(c ) angular acceleration of the sphere
View Solution