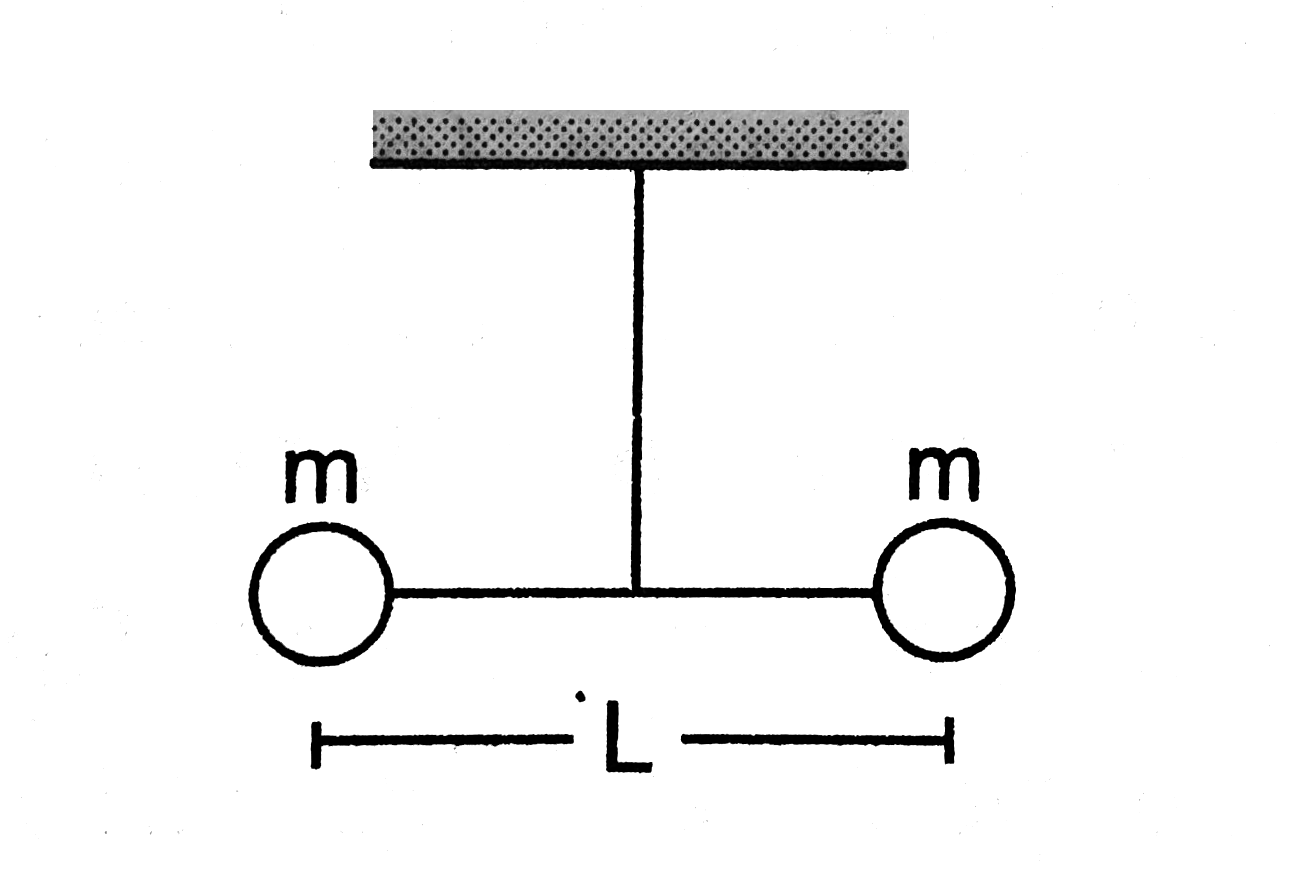
Two small balls, each of mass m are connected by a light rigid rod of length L. The system is suspended from its centre by a thin wire of torsional constant k. The rod is rotated about the wire through an angle θ0 and released. Find the tension in the rod as the system passes through the mean position.
The correct Answer is:A, B, D
The M.I. of the two ball system
I=2m(L2)2=mL22

At any position θ during the oscillation
→rque=kθ
So, work done during the displacement 0→θ0.
ω=∫θ00kθdthη=kθ202
By work energy method
12Iω2−0=workdo≠=kθ202
∴=kθ2I=kθ20mL2

Now from the free body diagram of the rod
T2=√(mω2L)2+(mg)2
=√mkθ20mL2×L2⎞⎟⎠+m2g2
=⎛⎜
⎜⎝√k2θ20L2+m2g2⎞⎟
⎟⎠
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
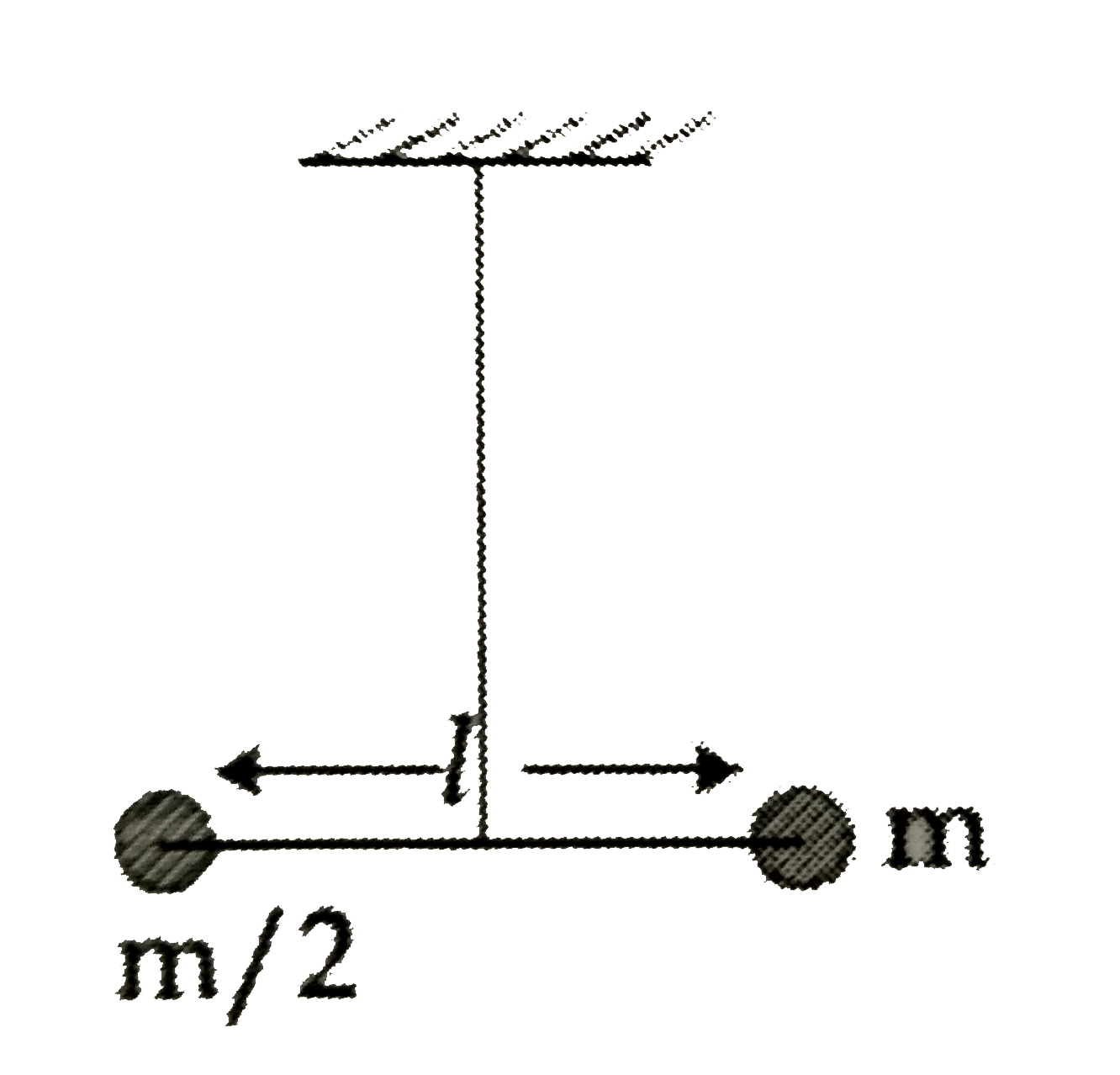
Two masses m and m2 are connected at the two ends of a massless rigid rod of length l. The rod is suspended by a thin wire of torsional constant k at the centre of mass of the rod-mass system(see figure). Because of torsional constant k, the restoring torque is τ=kθ for angular displacement θ. If the rod is rotated by θ0 and released, the tension in it when it passes through its mean position will be :
View SolutionTwo point masses m and 4m are connected by a light rigid rod of length l at the opposite ends. Moment of inertia of the system about an axis perpendicular to the length and passing through the centre of mass is
View Solution
Knowledge Check
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2
Two beads each of mass m are welded at the ends of two light rigid rods each of length l. if the pivots are smooth, find the ratio of translational and rotational kinetic energy of system.
View SolutionTwo small balls A and B of positive charge Q each and masses m and 2m, respectively, are connected by a nonconducting light rod of length L. This system is released in a uniform electric field of strength E as shown. Just after the release (assume no other force acts on the system)
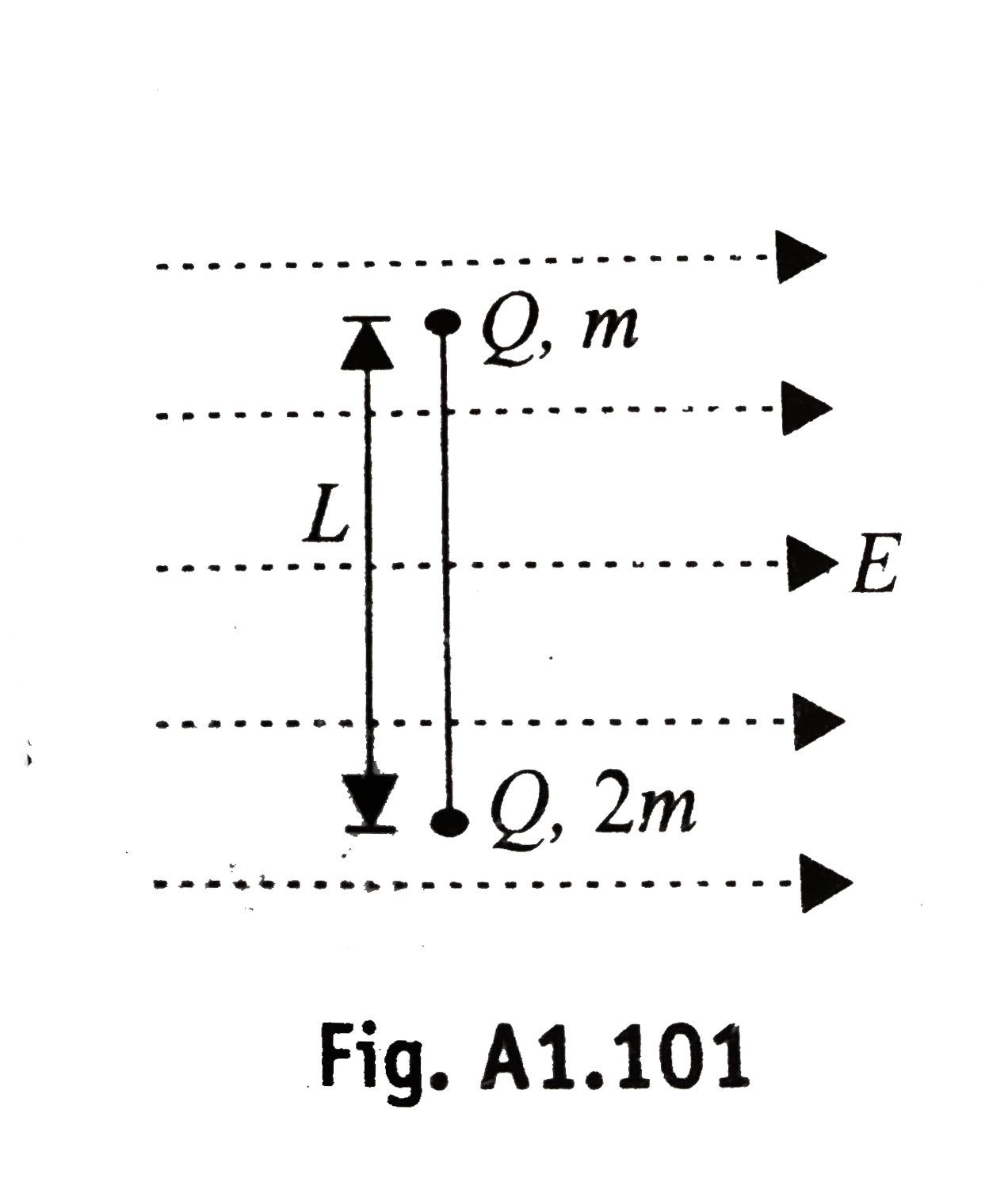
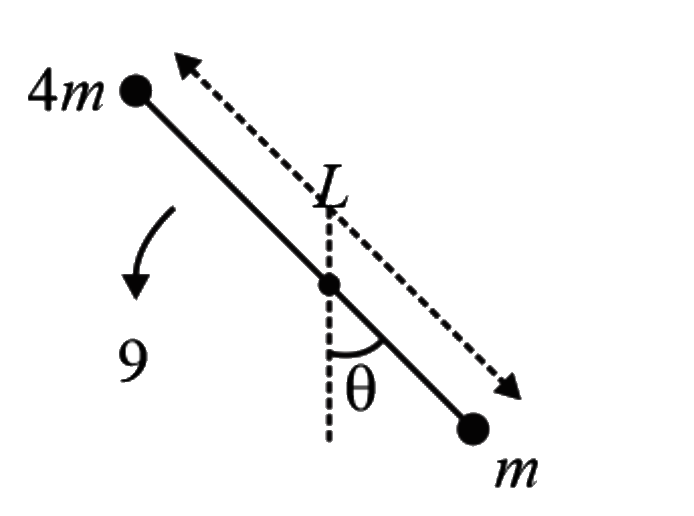
View SolutionTwo balls of mass m and 4m are connected by a rod of length L. The mass of the rod is small and can be treated as zero . The size of the balls also can of the neglected . We also assume the centre of the rod is hinged ,but the rod can rotate about its centre in the vertical plane without friction . What is the gravity - induced angular acceleration of the rod when the angle between the rod and the vertical is θ as shown ?
View SolutionTwo small balls A and B each of mass m, are attached tightly to the ends of a light rod of length d. The structure rotates about the perpendicular bisector of the rod at an angular speed ω. Calculate the angular momentum of the individual balls and of the system about the axis of rotation.
View SolutionThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View SolutionTwo particles of masses m1andm2 are joined by a light rigid rod of length r. The system rotates at an angular speed ω about an axis through the centre of mass of the system and perpendicular to the rod. Show that the angular momentum of the system is L=μr2ω where μ is the reduced mass of the system defined as μ=m1m2m1+m2
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View Solution
