A satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1m long placed inn the satellite?
To solve the problem of determining the height of the mercury column in a barometer tube placed inside a satellite, we can follow these steps:
Step 1: Understand the conditions inside the satellite
The problem states that the air pressure inside the satellite is maintained at 76 cm of mercury. This pressure is equivalent to the atmospheric pressure on Earth.
Step 2: Analyze the barometer tube
A barometer tube is a device used to measure atmospheric pressure. Under normal conditions on Earth, a barometer filled with mercury will rise to a height of approximately 76 cm due to the atmospheric pressure exerted on the mercury.
Step 3: Consider the effect of gravity in the satellite
In a satellite, which is in free fall, the effective gravitational force (g) is essentially zero. This means that there is no weight of mercury acting downwards to balance the pressure exerted by the atmosphere inside the satellite.
Step 4: Determine the height of mercury in the barometer tube
Since the pressure inside the satellite is maintained at 76 cm of mercury, and there is no gravitational force to counteract this pressure, the mercury in the barometer tube will rise to fill the entire tube. Therefore, if the barometer tube is 1 meter long, the mercury will rise to the full height of the tube.
Conclusion
The height of the mercury column in the barometer tube placed in the satellite will be 1 meter.
Final Answer
The height of the mercury column in the barometer tube inside the satellite will be 1 meter.
---
The problem states that the air pressure inside the satellite is maintained at 76 cm of mercury. This pressure is equivalent to the atmospheric pressure on Earth.
A barometer tube is a device used to measure atmospheric pressure. Under normal conditions on Earth, a barometer filled with mercury will rise to a height of approximately 76 cm due to the atmospheric pressure exerted on the mercury.
In a satellite, which is in free fall, the effective gravitational force (g) is essentially zero. This means that there is no weight of mercury acting downwards to balance the pressure exerted by the atmosphere inside the satellite.
Since the pressure inside the satellite is maintained at 76 cm of mercury, and there is no gravitational force to counteract this pressure, the mercury in the barometer tube will rise to fill the entire tube. Therefore, if the barometer tube is 1 meter long, the mercury will rise to the full height of the tube.
The height of the mercury column in the barometer tube placed in the satellite will be 1 meter.
The height of the mercury column in the barometer tube inside the satellite will be 1 meter.
Topper's Solved these Questions
Similar Questions
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass135∘ and surface tension of mercury =0.466Nm−1. Density of mercury=13600kgm−3.
View SolutionExplain how is the height of mercury column in the tube of a simple barometer, a measure of the atmospheric pressure.
View SolutionA barometer correctly reads the atmospheric pressure as 76cm of mercury. Water droplets are slowly introduced into the barometer tube by a dropper. The height of the mercury column first decreases and then become constant. If the saturation vapour pressure at the atmospheric temperature is 0.80cm of mercury, find the height if the mercury column when it reaches its minimum value.
View SolutionOne litre of air at 76 cm of mercury is compressed to a pressure of 152 cm of mercury under isothermal conditions. What is the new volume ?
View SolutionIf water be used to construct a barometer, what would be the height of water column at a standard atmospheric presure (76cm of mercury)?
View SolutionAn ideal gas is kept in a long cylindrical vessel fitted with a frictionless piston of cross-sectional area 10cm2and weight 1kg. The length of the gas column in the vessel now taken into a spaceship revolving round the earth as satellite. The air pressure in the spaceship is maintained at 100kPa. Find the length of the gas column in the cylinder.
View SolutionA satellite is to revolve round the earth in as circle of radius 8000 km. With what speed should this satellite be projected into orbit? What will be the time period?
Take g at the surface =9.8ms−2 and radius of the earth =6400 km.
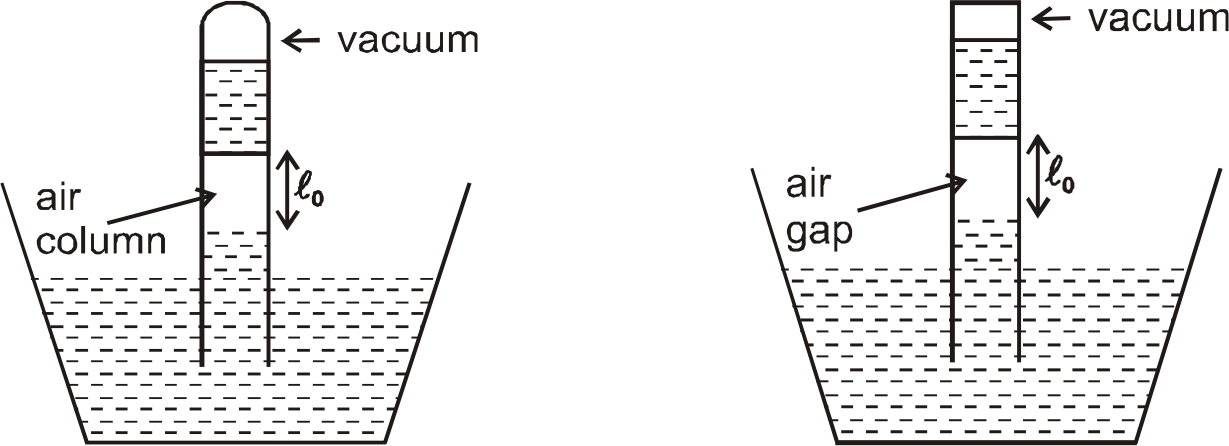
View SolutionAt the middle of the mercury barometer tube there is a little column of air with the length l0 and there is vacuum at the top as shown. Under the normal atmospheric pressure and the temperature of 200 le,vom/ l0=10cm. What will be the length of the air column if the temperature rises to 330 kelvin? (Neglict expansion of the tube)
View Solution
Artificial satellites go round the earth in their respective orbits. Astronauts are able to float in side the satellite. Inside space of the satellite could be treated as gravity free space. If a beaker filled with a liquid upto height h having a small hole in the bottom is placed in such a satellite, you will wonder te liquid does not come out of the hole. You have to squeeze or force the liquid to come out. suppose a constant pressure p is applied on the liquid through piston to force it out through the hole. Out side pressure could be neglected in comparison with p Cross-sectional area of beaker is too greater than that of hole (A>>a)
View SolutionAt a given place, a mercury barometer records a pressure of 0.70 m of Hg. What would be the height of water column if mercury in barometer is replaced by water? Take R.D. of mercury = 13.6.
View Solution
