A point object O is placed in fornt of a transparent slab at a distance x from its surface. It is seenfrom the other side of he slab by light incident nearlyl normally to the slab. The thickness of the slab is t and its refractive index is μ. Show that the apparent shift in the position of the object is independent of x and find its value.
To solve the problem, we need to determine the apparent shift in the position of a point object O placed in front of a transparent slab of thickness t and refractive index μ. The light is incident nearly normally to the slab.
1. Understanding the Setup:
- Let O be the point object placed at a distance x from the first surface of the slab.
- The slab has thickness t and refractive index μ.
- We need to find the apparent position of the object when viewed from the other side of the slab.
2. Refraction at the First Surface:
- When light travels from air (refractive index n1=1) to the slab (refractive index n2=μ), it bends towards the normal.
- Using the formula for refraction at a plane surface:
n2v−n1u=0
where v is the image distance from the first surface (let's denote it as ai1) and u is the object distance from the first surface (which is aO=x).
- Substituting the values, we get:
μai1=1x
- Rearranging gives:
ai1=μx
3. Refraction at the Second Surface:
- Now, the image i1 acts as a virtual object for the second surface of the slab.
- The distance from the second surface to the image i1 is t+ai1.
- Applying the refraction formula again:
1μ=bi2t+ai1
where bi2 is the image distance from the second surface.
- Substituting ai1=μx gives:
1μ=bi2t+μx
- Rearranging gives:
bi2=t+μxμ
4. Finding the Apparent Shift:
- The apparent shift S is given by the difference between the original object distance and the final image distance:
S=bO−bi2
- The distance bO (the distance from the second surface to the object) is t+x.
- Thus:
S=(t+x)−(t+μxμ)
- Simplifying this expression:
S=t+x−tμ−μxμ
S=t+x−tμ−x
S=t−tμ
S=t(1−1μ)
5. Conclusion:
- The apparent shift S is given by:
S=t(1−1μ)
- This shows that the apparent shift is independent of x.
- Let O be the point object placed at a distance x from the first surface of the slab.
- The slab has thickness t and refractive index μ.
- We need to find the apparent position of the object when viewed from the other side of the slab.
- When light travels from air (refractive index n1=1) to the slab (refractive index n2=μ), it bends towards the normal.
- Using the formula for refraction at a plane surface:
n2v−n1u=0
where v is the image distance from the first surface (let's denote it as ai1) and u is the object distance from the first surface (which is aO=x).
- Substituting the values, we get:
μai1=1x
- Rearranging gives:
ai1=μx
- Now, the image i1 acts as a virtual object for the second surface of the slab.
- The distance from the second surface to the image i1 is t+ai1.
- Applying the refraction formula again:
1μ=bi2t+ai1
where bi2 is the image distance from the second surface.
- Substituting ai1=μx gives:
1μ=bi2t+μx
- Rearranging gives:
bi2=t+μxμ
- The apparent shift S is given by the difference between the original object distance and the final image distance:
S=bO−bi2
- The distance bO (the distance from the second surface to the object) is t+x.
- Thus:
S=(t+x)−(t+μxμ)
- Simplifying this expression:
S=t+x−tμ−μxμ
S=t+x−tμ−x
S=t−tμ
S=t(1−1μ)
- The apparent shift S is given by:
S=t(1−1μ)
- This shows that the apparent shift is independent of x.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -1
15 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -2
7 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
Similar Questions
An object is seen through a glass slab of thickness 36cm and refractive index 3/2. The observer, and the slab are dipped in water (μ=4/3). The shift produced in the position of the object is
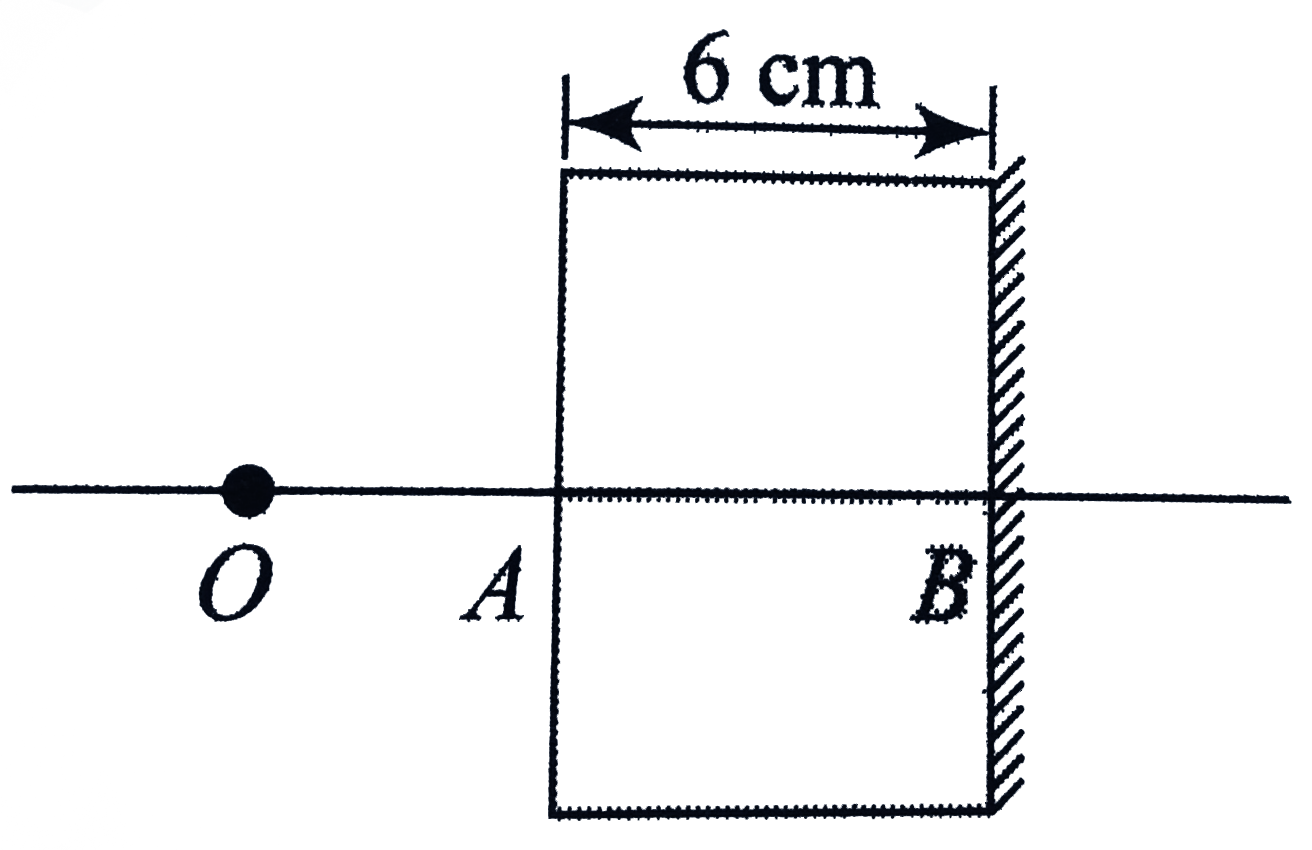
View SolutionAn object O is placed at 8cm in front of a glass slab, whose one face is silvered as shown in Figure. The thickness of the slab is 6cm. If the image formed 10 cm behind the silvered face, find the refractive index of glass.
View SolutionIn YDSE when slab of thickness t and refractive index μ is placed in front of one slit then central maxima shifts by one fringe width. Find out t in terms of λ and μ.
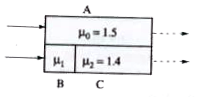
View SolutionA slab of transparent materials is made as shown in the figure. Monochromatic parallel beams of light are normally incident on the slabs. The thickness of C is twice the thickness of B. The number of waves is A= the number of waves in the combination of B and C. The refractive index of material A is μ0=1.5 and that of C is μ2=1.4
View SolutionFind the distance of object placed in the slab of refractive index μ from point P of the curved surface of radius R so that image is formed at infinity:

View SolutionA cubical transparent slab is used as a paper weight. What should be the minimum refractive index of the material of the slab so that letters below it are not visible from any of its vertical faces.
View Solution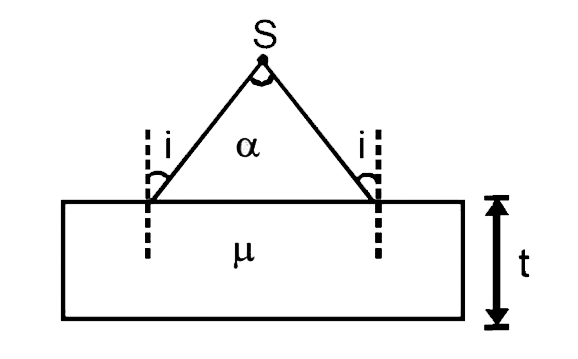
A diverging beam of light from a point source S having devergence angle α, falls symmetrically on a glass slab as shown. The angles of incidence of the two extreme rays are equal. If the thickness of the glass slab is t and the refractive index n, then the divergence angle of the emergent beam is
View SolutionDoes the escape speed of a body from the earth depend on.
(i)mass of the body
(ii)the location from where it is projected
(iii)the direction of projection
(iv)the height of the location from where the body is launched?
View SolutionA ray of light is incident on one face of a transparent slab of thickness 15 cm. The angle of incidence is 60∘. If the lateral displacement of the ray on emerging from the parallel plane is 5√3 cm, the refractive index of the material of the slab is
View SolutionTwo transparent slabs having equal thickness but different refractive indices μ1andμ2, are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits ?
View Solution
