The refractive indices of silicate fint glass for wavelength 400 nm and 700 nm are 1.66 aned 1.61 respectively. Find the minimum angles of deviation of an equailateral prism made of this glass for light of wavelength 400 nm and 700 nm.
To find the minimum angles of deviation of an equilateral prism made of silicate fint glass for light of wavelengths 400 nm and 700 nm, we can follow these steps:
Step 1: Understand the Problem
We are given the refractive indices of silicate fint glass for two different wavelengths of light (400 nm and 700 nm). The refractive indices are:
- For 400 nm: μ1=1.66
- For 700 nm: μ2=1.61
We need to find the minimum angle of deviation (D) for an equilateral prism, which has an apex angle A=60∘.
Step 2: Use the Formula for Minimum Angle of Deviation
For an equilateral prism, the relationship between the refractive index (μ), the angle of the prism (A), and the minimum angle of deviation (D) is given by:
μ=sin(A+D2)sin(A2)
Step 3: Substitute Known Values
Since the angle A for an equilateral prism is 60∘, we can substitute this into the equation.
First, calculate sin(A2):
A2=60∘2=30∘⇒sin(30∘)=12
Now, we can rewrite the equation for both wavelengths:
1. For μ1=1.66:
1.66=sin(30∘+D12)12⇒sin(30∘+D12)=1.66⋅12=0.83
2. For μ2=1.61:
1.61=sin(30∘+D22)12⇒sin(30∘+D22)=1.61⋅12=0.805
Step 4: Solve for D1 and D2
Now we need to find D1 and D2 for both cases.
1. For D1:
30∘+D12=sin−1(0.83)
Calculating sin−1(0.83):
sin−1(0.83)≈56.44∘
Thus,
D12=56.44∘−30∘=26.44∘⇒D1=2×26.44∘≈52.88∘
2. For D2:
30∘+D22=sin−1(0.805)
Calculating sin−1(0.805):
sin−1(0.805)≈53.13∘
Thus,
D22=53.13∘−30∘=23.13∘⇒D2=2×23.13∘≈46.26∘
Final Answers
- Minimum angle of deviation for 400 nm: D1≈52.88∘
- Minimum angle of deviation for 700 nm: D2≈46.26∘
We are given the refractive indices of silicate fint glass for two different wavelengths of light (400 nm and 700 nm). The refractive indices are:
- For 400 nm: μ1=1.66
- For 700 nm: μ2=1.61
For an equilateral prism, the relationship between the refractive index (μ), the angle of the prism (A), and the minimum angle of deviation (D) is given by:
Since the angle A for an equilateral prism is 60∘, we can substitute this into the equation.
A2=60∘2=30∘⇒sin(30∘)=12
1.66=sin(30∘+D12)12⇒sin(30∘+D12)=1.66⋅12=0.83
1.61=sin(30∘+D22)12⇒sin(30∘+D22)=1.61⋅12=0.805
Now we need to find D1 and D2 for both cases.
30∘+D12=sin−1(0.83)
Calculating sin−1(0.83):
sin−1(0.83)≈56.44∘
Thus,
D12=56.44∘−30∘=26.44∘⇒D1=2×26.44∘≈52.88∘
30∘+D22=sin−1(0.805)
Calculating sin−1(0.805):
sin−1(0.805)≈53.13∘
Thus,
D22=53.13∘−30∘=23.13∘⇒D2=2×23.13∘≈46.26∘
- Minimum angle of deviation for 400 nm: D1≈52.88∘
- Minimum angle of deviation for 700 nm: D2≈46.26∘
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -115videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
The refractive indices of flint glass for red and violet lights are 1.613 and 1.632, respectively. Find the angular dispersion produced by a thin prism of flint glass having refracting angle 5∘.
View SolutionThe refractive indices of flint glass for red and violet light are 1.613 and 1.632, respectively. Find the angular dispersion produced by the thin prism of flint glass having refracting angle 4∘.
View SolutionThe refractive indices of filnt glass for red and violet light are 1.613 and 1.632 respectively. Find the angular dispersion prouduced by a thin prism of flint glass having refracting angle 5∘
View SolutionThe refractive indices of the crown glass for violet and red lights are1.51and 1.49respectively and those of the flint glass are1.77and1.73respectively A prism of angle 6∘is made of crown glass .A beam of white light is incident at a small angle on this prism.The other thin flint glass prism is combined white the crown glass prism such that te net mean deviation is1.5∘anticlockwise.
(i)Determine the angle of the flint glass prism.
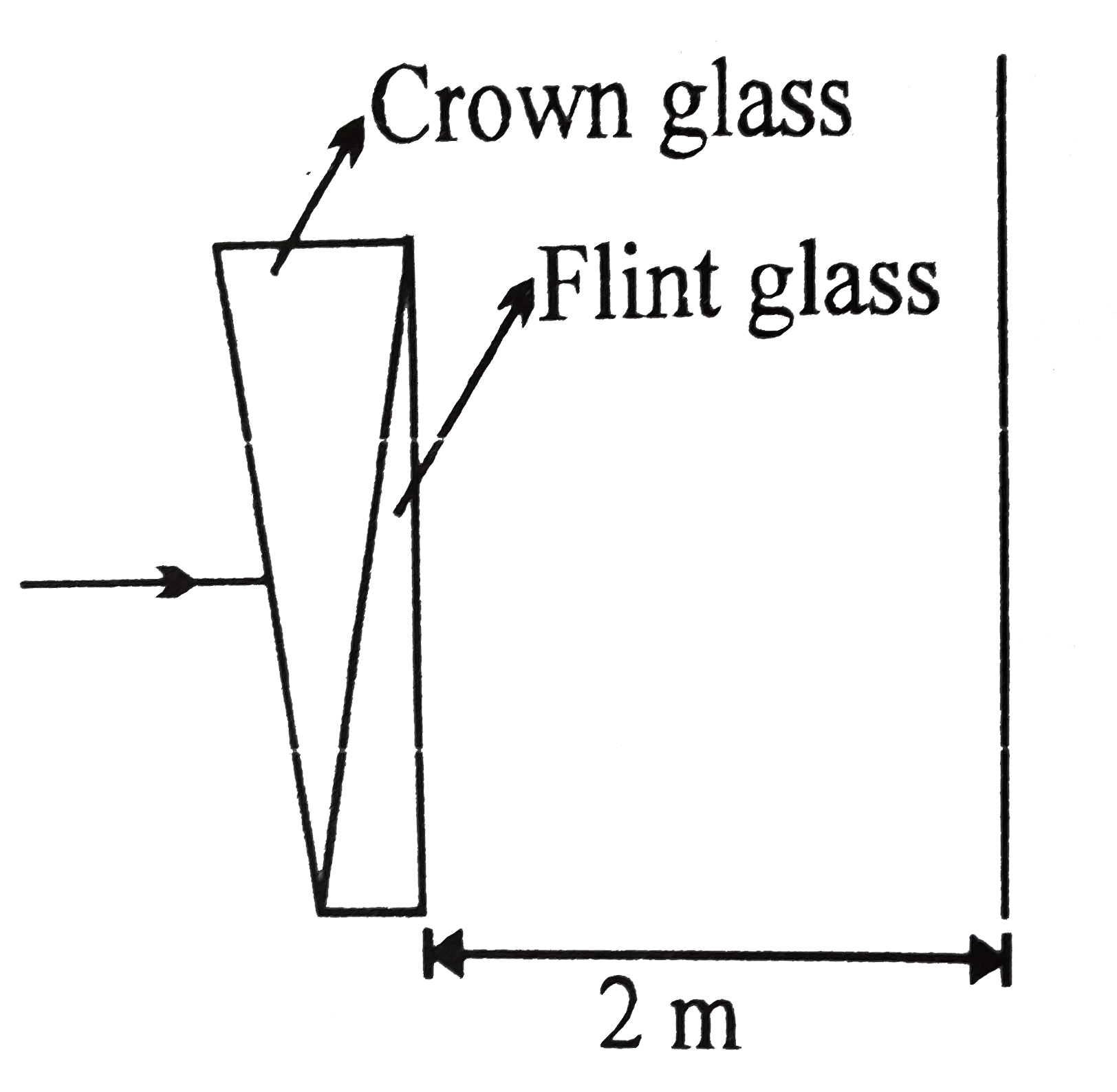
(ii)A screen is placed normal to the emerging beam at a distance of2mfrom the prism combination.find the distance between red and violet spot on the screen Which is the topmost colour on screen.View SolutionThe refractive index of a glass is 1.520 for red light and 1.525 for blue light. Let D1 and D2 be angles of minimum deviation for red and blue light respectively in a prism of this glass. Then,
View SolutionLight has a wavelength 600 nm in free space. it passes into the glass , which has an index of refraction of 1.50 what is the frequency of the light inside the glass?
View SolutionCalculate angle of minimum deviation (δm) for a regular glass prism. (Refractive index of glass = 1 6)
View SolutionIn this problem , which wavelength (s) will have a strong intensity if light have wavelength 400 nm-700 nm?
 View Solution
View SolutionThe index of refraction of heavy flint glass is 1.68 at 434nm and 1.65 at 671nm. Calculate the difference in the angle of deviation of blue (434nm) and red (671nm) light incident at 65∘ on one side of a heavy flint glass prism with apex angle 60∘.
View SolutionAn equilateral glass prism is made of a material of refractive index 1.500. Find its angle of minimum deviation.
View Solution

