The index of refraction of heavy flint glass is 1.68 at 434nm and 1.65 at 671nm. Calculate the difference in the angle of deviation of blue (434nm) and red (671nm) light incident at 65∘ on one side of a heavy flint glass prism with apex angle 60∘.
The correct Answer is:B
To solve the problem of calculating the difference in the angle of deviation of blue (434 nm) and red (671 nm) light incident at 65° on a heavy flint glass prism with an apex angle of 60°, we will follow these steps:
Step 1: Calculate the angle of refraction for blue light (R1)
Using Snell's Law:
μ=sinIsinR
Where:
- μ is the refractive index of the glass for blue light (1.68),
- I is the angle of incidence (65°),
- R1 is the angle of refraction for blue light.
Rearranging gives:
sinR1=sinIμ
Substituting the values:
sinR1=sin65°1.68
Calculating R1:
R1≈32.6°
Step 2: Calculate the angle of refraction for red light (R1)
Using the same approach for red light with a refractive index of 1.65:
sinR1=sin65°1.65
Calculating R1:
R1≈33.3°
Step 3: Calculate the second angle of refraction (R2) for both colors
Using the formula for the angles in a prism:
R2=A−R1
Where A is the apex angle of the prism (60°).
For blue light:
R2blue=60°−32.6°=27.4°
For red light:
R2red=60°−33.3°=26.7°
Step 4: Calculate the angle of incidence at the second face (I2)
Using Snell's Law again:
sinI2=μ⋅sinR2
For blue light:
sinI2blue=1.68⋅sin27.4°
Calculating I2blue:
I2blue≈50.6°
For red light:
sinI2red=1.65⋅sin26.7°
Calculating I2red:
I2red≈47.8°
Step 5: Calculate the angle of deviation for both colors
The angle of deviation D is given by:
D=I1+I2−A
For blue light:
Dblue=65°+50.6°−60°=55.6°
For red light:
Dred=65°+47.8°−60°=52.8°
Step 6: Calculate the difference in the angle of deviation
ΔD=Dblue−Dred
Calculating the difference:
ΔD=55.6°−52.8°=2.8°
Thus, the difference in the angle of deviation of blue and red light is 2.8°.
---
Using Snell's Law:
μ=sinIsinR
Where:
- μ is the refractive index of the glass for blue light (1.68),
- I is the angle of incidence (65°),
- R1 is the angle of refraction for blue light.
sinR1=sinIμ
Substituting the values:
sinR1=sin65°1.68
Calculating R1:
R1≈32.6°
Using the same approach for red light with a refractive index of 1.65:
sinR1=sin65°1.65
Calculating R1:
R1≈33.3°
Using the formula for the angles in a prism:
R2=A−R1
Where A is the apex angle of the prism (60°).
R2blue=60°−32.6°=27.4°
R2red=60°−33.3°=26.7°
Using Snell's Law again:
sinI2=μ⋅sinR2
sinI2blue=1.68⋅sin27.4°
Calculating I2blue:
I2blue≈50.6°
sinI2red=1.65⋅sin26.7°
Calculating I2red:
I2red≈47.8°
The angle of deviation D is given by:
D=I1+I2−A
Dblue=65°+50.6°−60°=55.6°
Dred=65°+47.8°−60°=52.8°
ΔD=Dblue−Dred
Calculating the difference:
ΔD=55.6°−52.8°=2.8°
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions8videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Level 2 Single Correct41videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Objective Questions1videos
REFRACTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective12videos
SEMICONDUCTORS
Similar Questions
The refractive index of a glass is 1.520 for red light and 1.525 for blue light. Let D1 and D2 be angles of minimum deviation for red and blue light respectively in a prism of this glass. Then,
View Solution(a) Deduce the expression, by drawing a suitable ray diagram, for the refractive index of a triangular glass prisms in terms of the angle of minimum deviation (D) and the angle of prism (A).
Draw a plot showing the variation of the angle of deviation with the angle of incidence.
(b) Calculate the value of the angle of incidence when a ray of light incident on one face of an equilateral glass prism produces the emergent ray, which just grazes along the adjacent face. Refractive index of prism is √2View SolutionAn equilateral glass prism is made of a material of refractive index 1.500. Find its angle of minimum deviation.
View SolutionThe refractive indices of silicate fint glass for wavelength 400 nm and 700 nm are 1.66 aned 1.61 respectively. Find the minimum angles of deviation of an equailateral prism made of this glass for light of wavelength 400 nm and 700 nm.
View SolutionThe refractive indices of the crown glass for violet and red lights are1.51and 1.49respectively and those of the flint glass are1.77and1.73respectively A prism of angle 6∘is made of crown glass .A beam of white light is incident at a small angle on this prism.The other thin flint glass prism is combined white the crown glass prism such that te net mean deviation is1.5∘anticlockwise.
(i)Determine the angle of the flint glass prism.
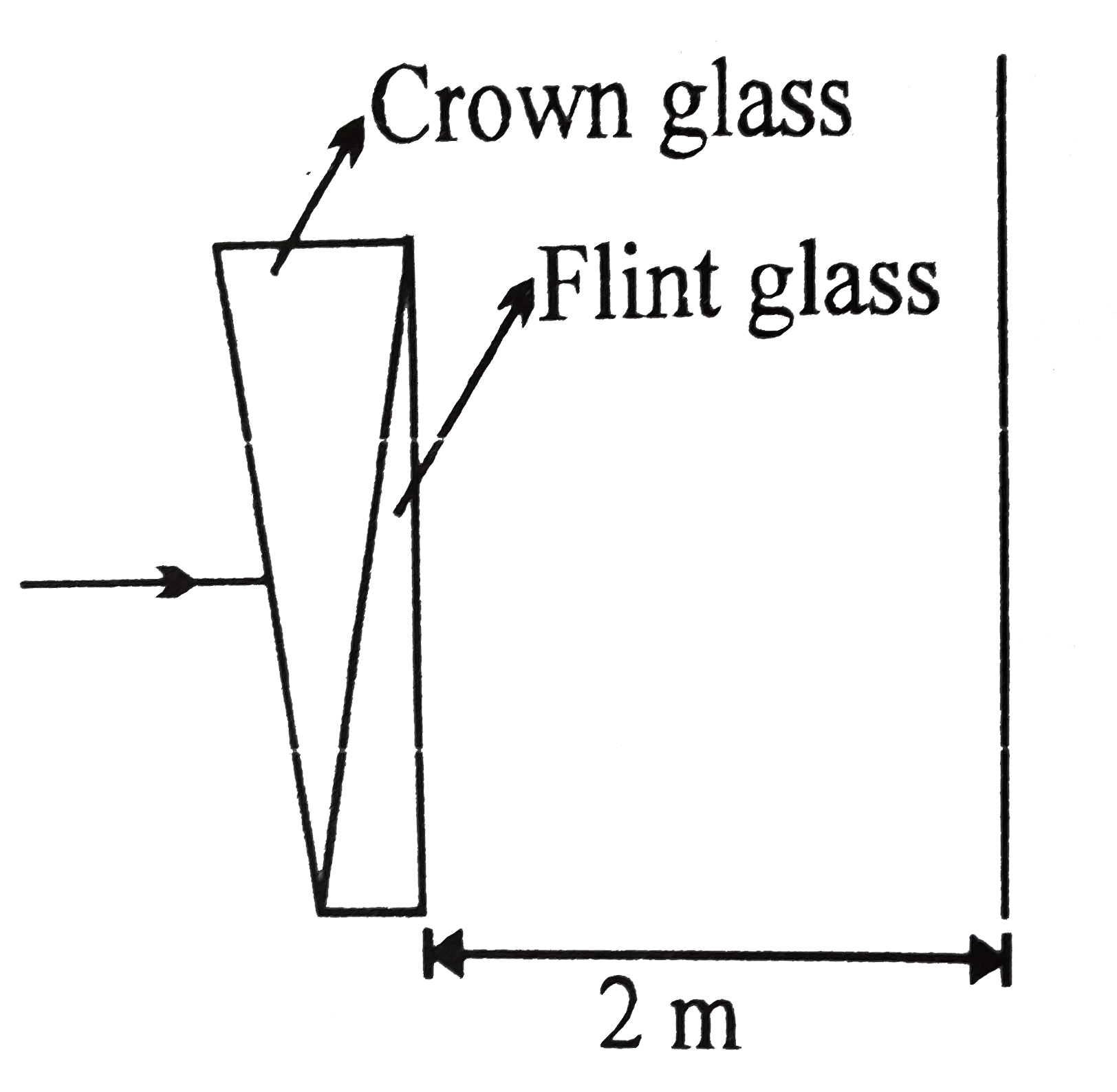
(ii)A screen is placed normal to the emerging beam at a distance of2mfrom the prism combination.find the distance between red and violet spot on the screen Which is the topmost colour on screen.View SolutionA ray of light is incident normally on one of the faces of a prism of apex angle 30 degree and refractive index √2. The angle of deviation of the ray in degrees is
View SolutionA ray of light passes from glass, having a refractive index of 1.6, to air. The angle of incidence for which the angle of refraction is twice the angle of incidence is
View SolutionAn equilateral glass prism has a refrective index 1.6 in air. Calculate the angle of minimum deviation of the prism, when kept in a medium of refractive index 4√25.
View SolutionThe least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is 1.5. Then the angle of the prism is
View SolutionThe least angle of deviation for a glass prism is equal to its refracting angle. The refractive index of glass is 1.5. Then the angle of the prism is
View Solution

