A small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t<dV, (b) at a time t>dV.
The correct Answer is:A, B, D
To solve the problem step by step, we need to analyze the motion of the block and the mirror, as well as the properties of the concave mirror.
Step 1: Understanding the Initial Setup
We have a block of mass m and a concave mirror with radius R on a smooth horizontal table, separated by a distance d. The block is moving towards the mirror with a constant speed V.
Step 2: Determine Object Distance Before Collision
At time t, the distance of the block from the mirror can be expressed as:
u=−(d−Vt)
This is because the object distance u is taken as negative in the mirror formula convention, and the block is moving towards the mirror.
Step 3: Calculate Focal Length of the Mirror
The focal length f of a concave mirror is given by:
f=−R2
Step 4: Apply the Mirror Formula
Using the mirror formula:
1f=1v+1u
Substituting the values of f and u:
1−R2=1v+1−(d−Vt)
This simplifies to:
−2R=1v−1(d−Vt)
Step 5: Solve for Image Distance v
Rearranging gives:
1v=−2R+1(d−Vt)
1v=(d−Vt)−(−2R)R(d−Vt)
v=R(d−Vt)(d−Vt)+2R
Step 6: Find the Velocity of the Image for t<dV
For t<dV, the block has not yet collided with the mirror. The velocity of the image vi can be found by differentiating v with respect to time t:
dvdt=ddt(R(d−Vt)(d−Vt)+2R)
Using the quotient rule, we can find dvdt.
Step 7: Collision and Post-Collision Analysis
When the block collides with the mirror, since the collision is perfectly elastic, the block will come to rest, and the mirror will move with velocity V.
Step 8: Determine Object Distance After Collision
After the collision, the object distance u becomes:
u=d−Vt
for t>dV.
Step 9: Apply the Mirror Formula Again
Using the same mirror formula:
1v=−2R+1(d−Vt)
We can solve for v again.
Step 10: Final Velocity of the Image
The final velocity of the image after the collision can be expressed as:
vi=velocity of the mirror+velocity of the image due to the mirror
Summary of Results
- For t<dV: The velocity of the image can be calculated using the derived formula.
- For t>dV: The velocity of the image will be influenced by the motion of the mirror and can be calculated similarly.
We have a block of mass m and a concave mirror with radius R on a smooth horizontal table, separated by a distance d. The block is moving towards the mirror with a constant speed V.
At time t, the distance of the block from the mirror can be expressed as:
u=−(d−Vt)
This is because the object distance u is taken as negative in the mirror formula convention, and the block is moving towards the mirror.
The focal length f of a concave mirror is given by:
f=−R2
Using the mirror formula:
1f=1v+1u
Substituting the values of f and u:
1−R2=1v+1−(d−Vt)
This simplifies to:
−2R=1v−1(d−Vt)
Rearranging gives:
1v=−2R+1(d−Vt)
1v=(d−Vt)−(−2R)R(d−Vt)
v=R(d−Vt)(d−Vt)+2R
For t<dV, the block has not yet collided with the mirror. The velocity of the image vi can be found by differentiating v with respect to time t:
dvdt=ddt(R(d−Vt)(d−Vt)+2R)
Using the quotient rule, we can find dvdt.
When the block collides with the mirror, since the collision is perfectly elastic, the block will come to rest, and the mirror will move with velocity V.
After the collision, the object distance u becomes:
u=d−Vt
for t>dV.
Using the same mirror formula:
1v=−2R+1(d−Vt)
We can solve for v again.
The final velocity of the image after the collision can be expressed as:
vi=velocity of the mirror+velocity of the image due to the mirror
- For t<dV: The velocity of the image can be calculated using the derived formula.
- For t>dV: The velocity of the image will be influenced by the motion of the mirror and can be calculated similarly.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXAMPLE9videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer18videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Objective -27videos
GEOMETRICAL OPTICS
- BOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question7videos
GAUSS LAW
- BOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer11videos
LIGHT WAVES
Similar Questions
An object is moving towards a convex mirror with a constant velocity. P is the pole of mirror.
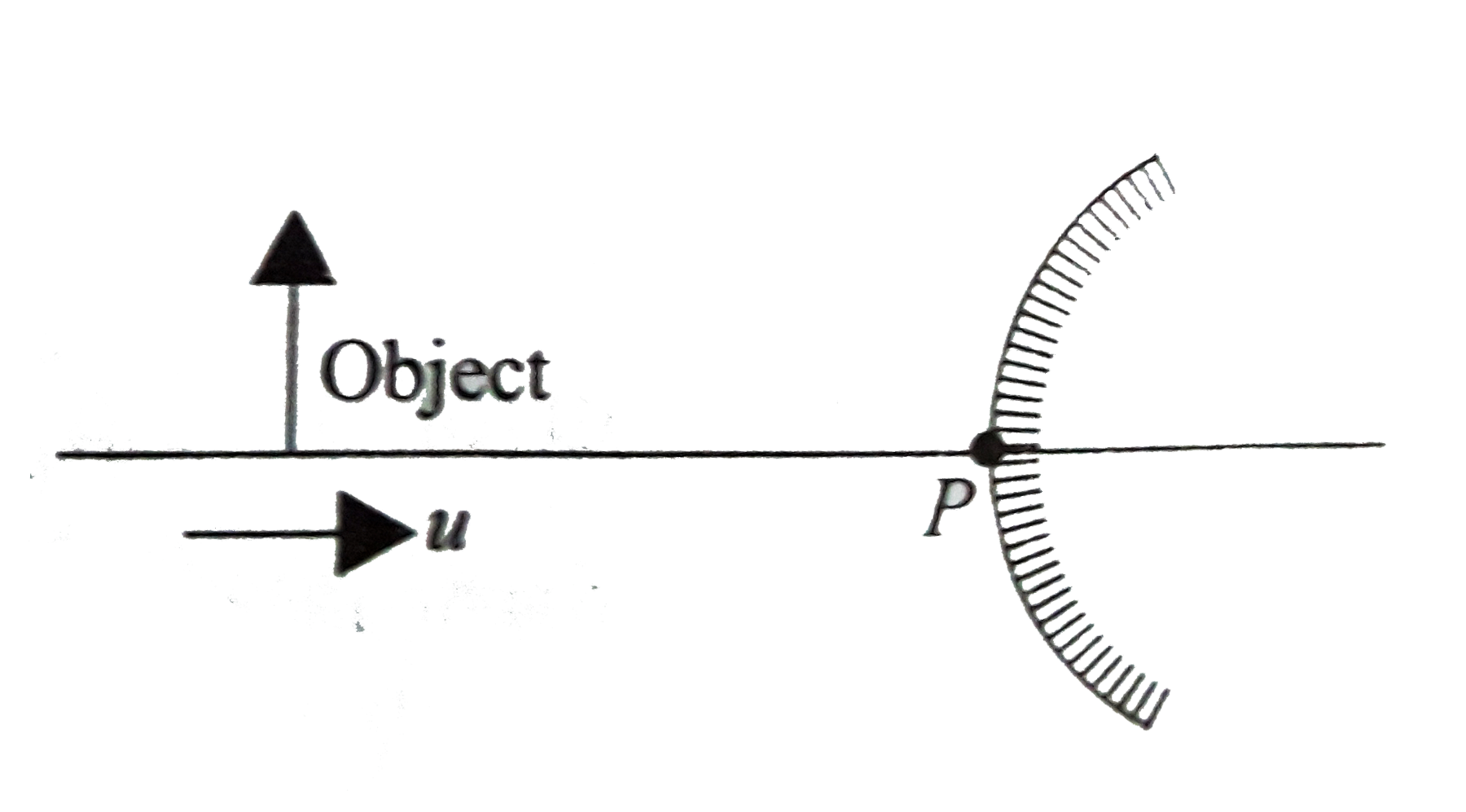 View Solution
View SolutionWe use concave mirrors as rear view mirrors.
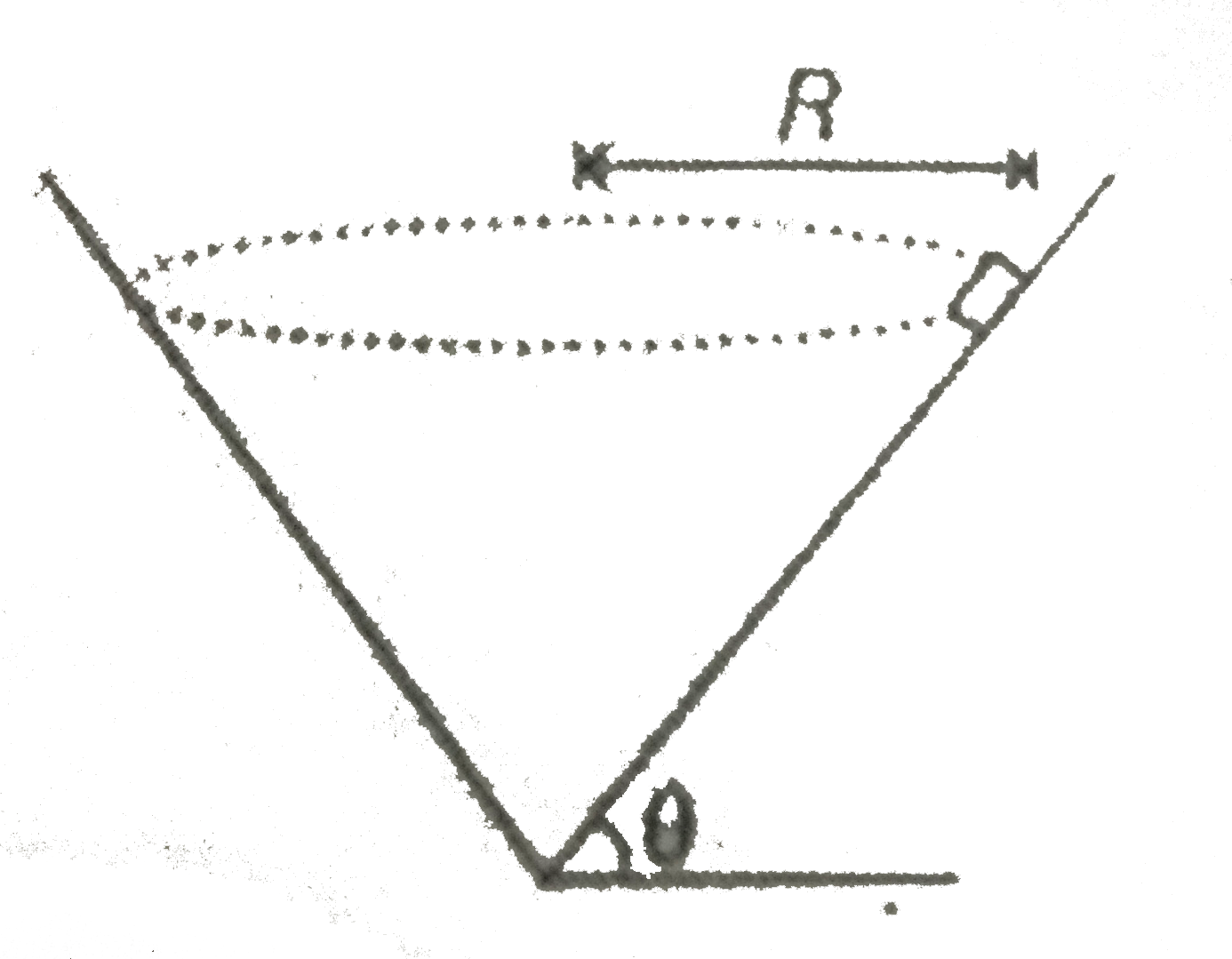
View SolutionA block of mass m is moving in a circle of radius R with speed v inside a smooth cone as shown in figure. Choose the wrong options
 View Solution
View SolutionA point object is moving on the principal axis of a concave mirror of focal length 24cm towards the mirror. When it is at a distance of 60cm from the mirror, its velocity is . 9sec/cm What is the velocity of the image at that instant
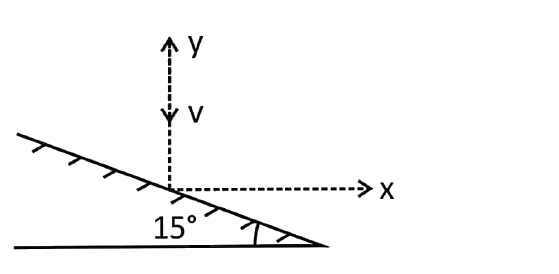
View SolutionAn object is moving towards a mirror with a velocity of 10ms−1 as shown in the figure. If the collision between the mirror and the object is perfectly elastic, then the velocity of the image after collision with mirror in vector form is
 View Solution
View SolutionThree masses A, B and C are kept on a smooth horizontal surface as shown in the fiugre. A sharp impulse is given to the mass A, so that it starts moving towards B with speed v0. What is the minimum value of m so that there is only one collision between masses A and B (all collisions are elastic)
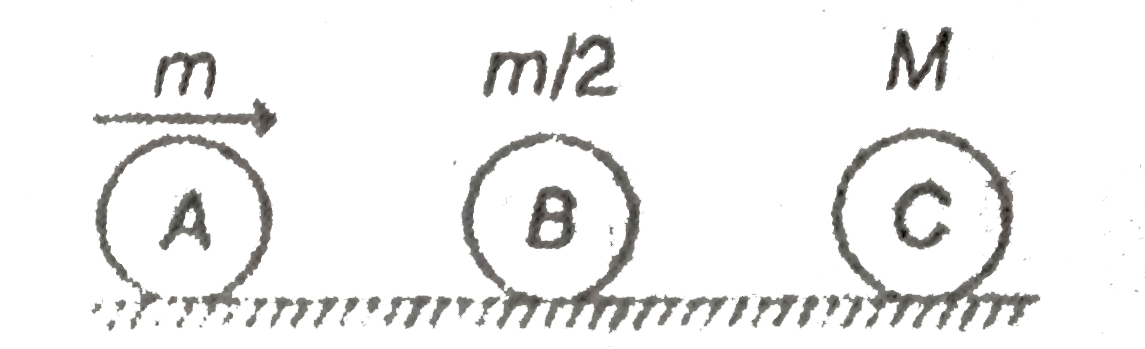 View Solution
View SolutionA person moves with a velocity v towards a plane mirror. With what velocity does his image move towards him ?
View SolutionA man runs towards a mirror at a speed 15 m/s. The speed of the image relative to the man is
View SolutionA real object is placed in front of a convex mirror (fixed).The object is moving toward the mirror. If v0 is the speed of object and vi is the speed of image, then
View SolutionA block of mass m is revolving in a smooth horizontal plane with a constant speed v.If the radius of the circle path is R find the total contact force received by the block
 View Solution
View Solution

