Question

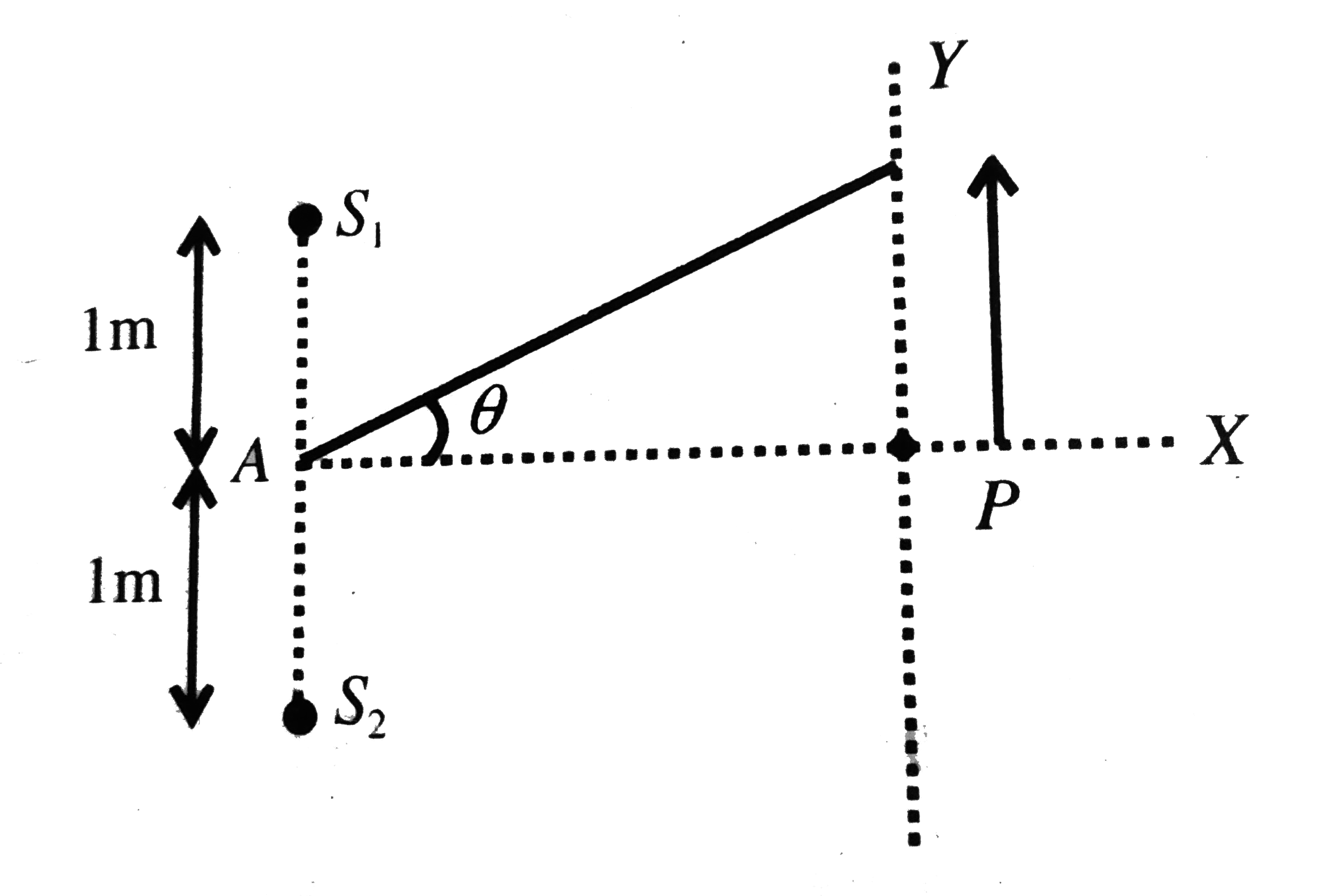
Two speakers ${\displaystyle S_1\text{and}{S}_2}$ derived by the same amplifier and placed at ${\displaystyle y=1.0m\text{and}y=-1.0m}$ (Fig . 7.9) The speakers vibrate in phase at ${\displaystyle 600Hz}$. A man stands at a point on the x - axis at a very large distance from the origin and starts moving parallel to the Y - axis . The speed of sound in air is ${\displaystyle 330m/s}$.
(a). At what angle will the intensity of sound drop to a minimum for the first time ?
(b) At what angle will the sound intensity be maximum for the first time ?
(c ) If he continues to walk along the line , how many more maxima can he hear ?

Answer

A::B::C

Explanation

Given `f=600 Hz and v=330 m/s`
`rarr lamda=v/f=330/660=0.5mm`
Let OP=D, PQ=y
`rarr theta=y/r`…..i
Now path difference is given by
`x=S_2Q-S_1Q=(yd)/D`
where d=2`
`[the proof of x=(yd)/D` is discussed in interference of light waves]`
a.for minimum intensity
`x=(2n+1)(lamda/2)`
`:. (yd)/2=lamda/2 [for minimum y,x=lamda/2]`
`:. (yd)/D=theta=lamda/(2d)`
`0.55/4=0.1375rad`
`=0.1375xx(57.1)^@=7.9^@`
b. for minimum intensity
`x=2n(lamda/2)`
`(yd)/D=lamda`
`rarr lamda(D-theta)=lamda/d`
`=00.55/2=0.275rad`
`:. thet= 16^@`
c. For more maxima` (yd)/D=2lamda, 3lamda, 4 lamda,..........`
`rarr y/D=theta=32^@, 64^@, 128^@`
But since the maximum vlaue of theta can be `90^@` he will hear two more maximum i.e. at `32^@ and 64^@`.