A dielectric slab is inserted between the plates of an isolatted charged capacitor. Which of the following quantities will remain the same?
The electric field in the capacitor
The charge on the capacitor
The cpotential difference between the plates
The stored energy in the capacitor
The correct Answer is:B
To solve the problem, we need to analyze the effect of inserting a dielectric slab into an isolated charged capacitor. We will evaluate each of the given options to determine which quantity remains unchanged.
1. Understanding the System:
- We have an isolated charged capacitor, meaning it is not connected to any external voltage source (battery). The charge on the capacitor plates is fixed.
2. Analyzing the Electric Field (E):
- The electric field (E) in a capacitor without a dielectric is given by the formula:
E=σϵ0
where σ is the surface charge density.
- When a dielectric slab is inserted, the electric field becomes:
E′=σϵ0K
where K is the dielectric constant of the material.
- Since K>1, it follows that E′<E. Therefore, the electric field decreases when the dielectric is inserted. Conclusion: Electric field changes.
3. Analyzing the Charge (Q):
- For an isolated capacitor, the charge Q on the plates remains constant because there is no external circuit to allow charge to flow. Conclusion: Charge remains the same.
4. Analyzing the Potential Difference (V):
- The potential difference V across the capacitor is given by:
V=QC
- When a dielectric is inserted, the capacitance increases to C′=KC0. Thus, the new potential difference becomes:
V′=QKC0
- Since K>1, it follows that V′<V. Therefore, the potential difference decreases. Conclusion: Potential difference changes.
5. Analyzing the Stored Energy (U):
- The energy stored in the capacitor is given by:
U=Q22C
- With the new capacitance C′=KC0, the energy becomes:
U′=Q22KC0
- Since K>1, it follows that U′<U. Therefore, the stored energy decreases. Conclusion: Stored energy changes.
Final Answer:
The quantity that remains the same when a dielectric slab is inserted between the plates of an isolated charged capacitor is the charge on the capacitor.
Summary of Results:
- Electric Field: Changes
- Charge: Remains the same
- Potential Difference: Changes
- Stored Energy: Changes
- We have an isolated charged capacitor, meaning it is not connected to any external voltage source (battery). The charge on the capacitor plates is fixed.
- The electric field (E) in a capacitor without a dielectric is given by the formula:
E=σϵ0
where σ is the surface charge density.
- When a dielectric slab is inserted, the electric field becomes:
E′=σϵ0K
where K is the dielectric constant of the material.
- Since K>1, it follows that E′<E. Therefore, the electric field decreases when the dielectric is inserted. Conclusion: Electric field changes.
- For an isolated capacitor, the charge Q on the plates remains constant because there is no external circuit to allow charge to flow. Conclusion: Charge remains the same.
- The potential difference V across the capacitor is given by:
V=QC
- When a dielectric is inserted, the capacitance increases to C′=KC0. Thus, the new potential difference becomes:
V′=QKC0
- Since K>1, it follows that V′<V. Therefore, the potential difference decreases. Conclusion: Potential difference changes.
- The energy stored in the capacitor is given by:
U=Q22C
- With the new capacitance C′=KC0, the energy becomes:
U′=Q22KC0
- Since K>1, it follows that U′<U. Therefore, the stored energy decreases. Conclusion: Stored energy changes.
The quantity that remains the same when a dielectric slab is inserted between the plates of an isolated charged capacitor is the charge on the capacitor.
- Electric Field: Changes
- Charge: Remains the same
- Potential Difference: Changes
- Stored Energy: Changes
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Exercise
65 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - Objective 1
12 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
When a dielectric slab is gradually inserted between the plates of an isolated parallel-plate capacitor , the energy of the system decreases.What can you conclude about the force on the slab exerted by the electric field?
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionOn placing dielectric slab between the plates of an isolated charged condenser its
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors in figure , which of the following properties increase ?
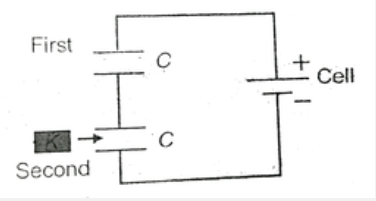
View SolutionThe separation between the plates of a charged parallel-plate capacitor is increased. Which of the following quantities will change?
View SolutionAssertion: A dielectric slabis inserted between plates of an isolated capacitor. charge on capacitor will remain same.
Reason Charge on an isolated system is conserved.
View SolutionA dielectric slab is inserted between the plates of a capacitor. The charge on the capacitor is Q and the magnitude of the induced charge on each surface of the dielectric is Q'.
View SolutionA parallel plate capacitor has plate of length 'l' width 'w' and separation of plates is 'd' . It is connected to a battery of emf V . A dielectric slab of the same thickness 'd' and of dielectric constant k=4 is being inserted between the plates of the capacitor . At what lenght of the slab inside plates , will the energy stored in the capacitor be two time the initial energy stored ?
View SolutionAssertion : Resonance frequency will decrease in L−C−R series circuit if a dielectric slab is inserted in between the plates of the capacitor.
Reason : By doing so, capacity of capacitor will increase.
View SolutionWhen a dielectric slab is inserted between the plates of one of the two identical capacitors shown in the figure then match the following:
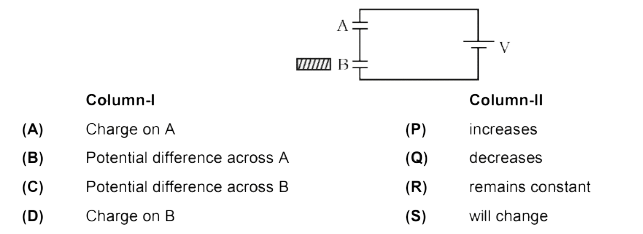
View Solution
