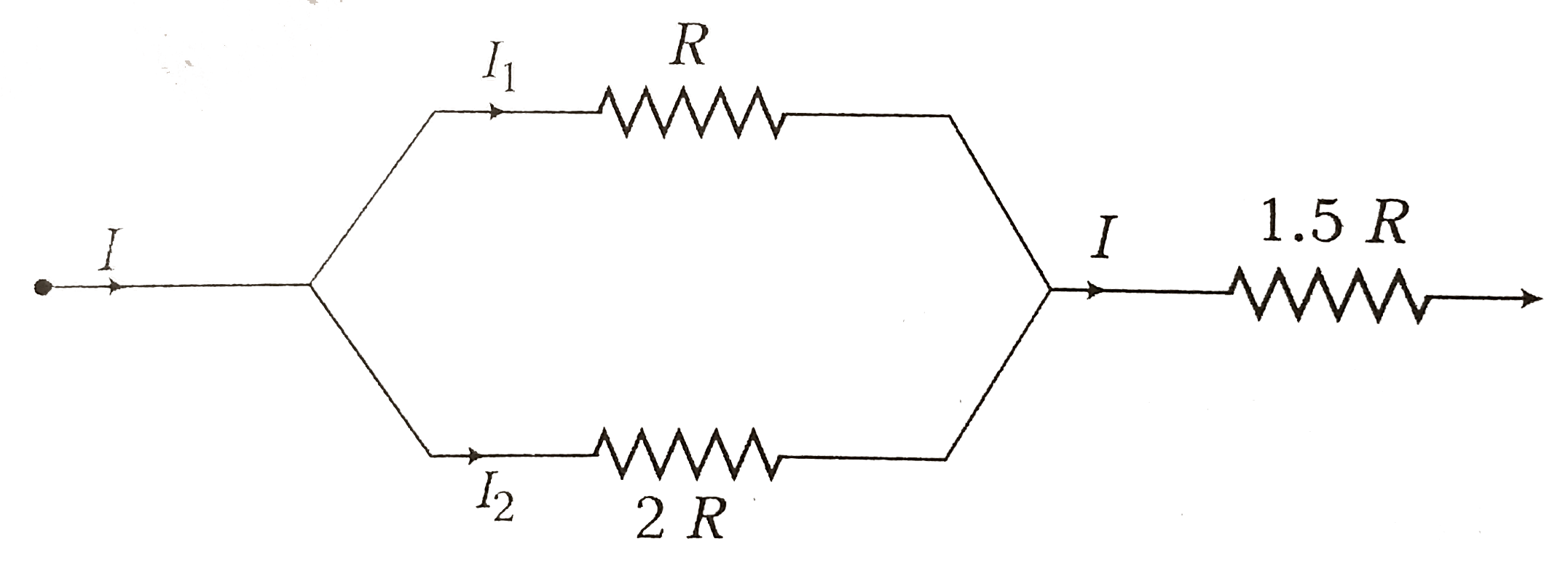
Two resistors R and 2R are connected in series in an electric circuit. The thermal energy developed in R and 2R are in the ratio
(a)1:2
(b)2:1
(c )1:4
(d)4:1
The correct Answer is:A
To find the ratio of thermal energy developed in resistors R and 2R connected in series, we can follow these steps:
1. Identify the Resistors and Their Values:
- Let the first resistor be R1=R.
- Let the second resistor be R2=2R.
2. Understand the Circuit Configuration:
- The resistors are connected in series across a potential difference V.
- In a series circuit, the same current I flows through both resistors.
3. Use the Formula for Heat Dissipation:
- The heat (thermal energy) developed in a resistor can be calculated using the formula:
H=I2RT
- Where H is the heat developed, I is the current, R is the resistance, and T is the time for which the current flows.
4. Calculate Heat Developed in Each Resistor:
- For resistor R1 (which is R):
H1=I2RT
- For resistor R2 (which is 2R):
H2=I2(2R)T=2I2RT
5. Find the Ratio of Heat Developed:
- To find the ratio H1H2:
H1H2=I2RT2I2RT
- Simplifying this gives:
H1H2=12
6. Conclusion:
- The ratio of thermal energy developed in resistors R and 2R is 1:2.
Final Answer:
The thermal energy developed in R and 2R are in the ratio 1:2.
---
- Let the first resistor be R1=R.
- Let the second resistor be R2=2R.
- The resistors are connected in series across a potential difference V.
- In a series circuit, the same current I flows through both resistors.
- The heat (thermal energy) developed in a resistor can be calculated using the formula:
H=I2RT
- Where H is the heat developed, I is the current, R is the resistance, and T is the time for which the current flows.
- For resistor R1 (which is R):
H1=I2RT
- For resistor R2 (which is 2R):
H2=I2(2R)T=2I2RT
- To find the ratio H1H2:
H1H2=I2RT2I2RT
- Simplifying this gives:
H1H2=12
- The ratio of thermal energy developed in resistors R and 2R is 1:2.
The thermal energy developed in R and 2R are in the ratio 1:2.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 2
9 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example
33 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
Knowledge Check
When resistors R1andR2 are connected in a parallel electric circuit, the total resistance is 11R1+1R2. This fraction is equivalent to
AR1+R2BR1+R2R1R2CR1R2+R2R1DR1R2R1+R2
When two resistances R1andR2 are connected in series , they consume 12 W powers . When they are connected in parallel , they consume 50 W powers . What is the ratio of the powers of R1andR2 ?
View SolutionWhat is the ratio of heat generated in R and 2R

View SolutionTwo unequal resistances R1andR2 ae connected across two identical batteries of emfε and internal resistance r(figure). Can the thermal energies developed in R1andR2 be equal in a given time. If yes, what will be the condition? (Figure Question)

View SolutionA parallel combination of an 8Ω resistor and an unknown resistor R is connected in series with a 16Ω resistor and a battery. This circuit is then disassembled, and the three resistors are then connected in series with each other oand the same battery. in both arrangements, the current through the 8Ω resistor is the same. What is the unknown resistance R?

View Solution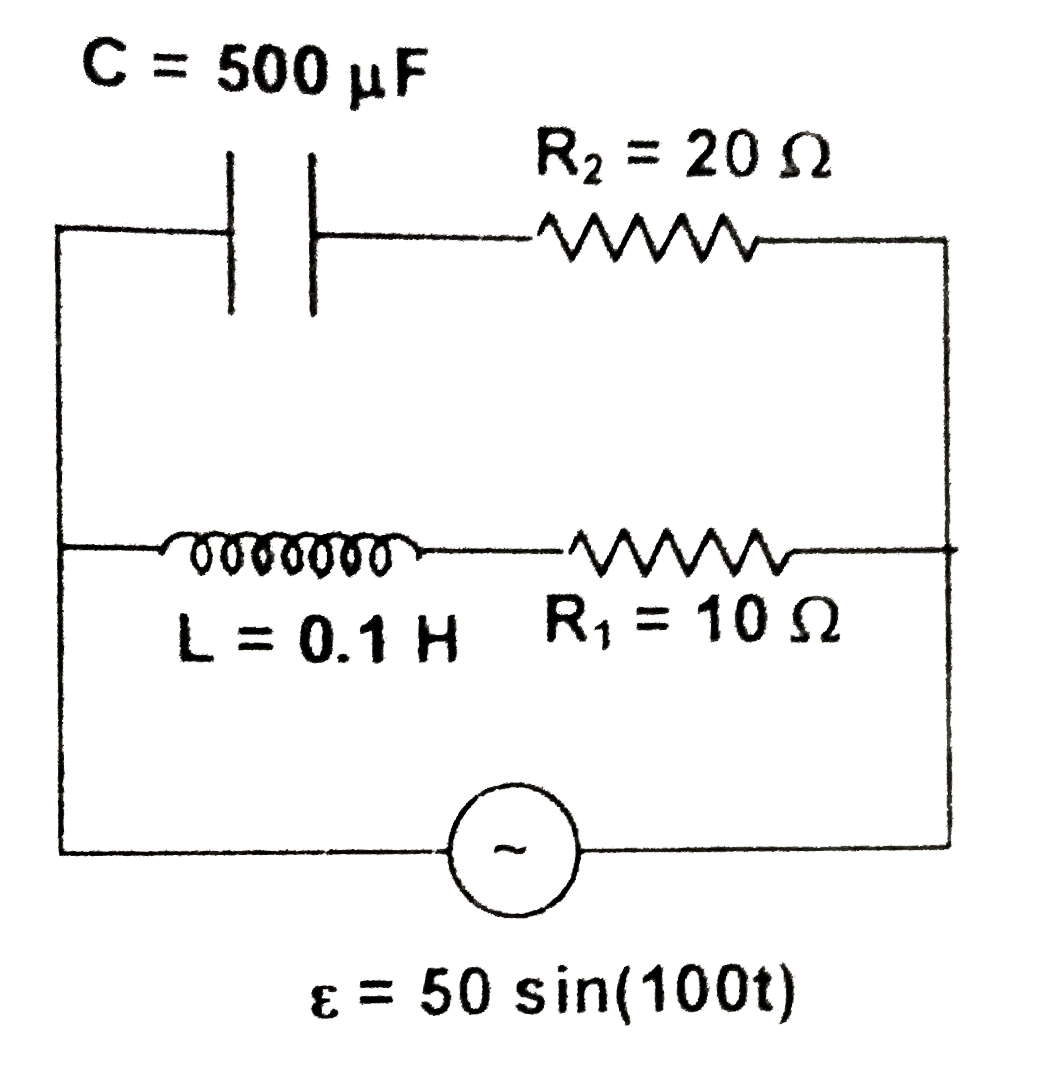
In the circuit shown the average power developed in the resistor R1 is
View SolutionTwo resistors R1=400ΩandR2=20Ω are connected in parallel to a battery. If heating power developed in R1 is 25. W. find the heating power developed in R2.
View SolutionThree resistors R1,R2 and R3 are to be combined to form an electrical circuit as shown in the figure. It is found that when R1R2andR3 are put respectively in positions A, B and C, the effective resistance of the circuit is 70 ΩWhen R2,R3andR1 are put respectively in position A, B and C the effective resistance is 35Ω and when R3,R1andR2 are respectively put in the position A, B and C, the effective resistance is 42Ω
If R1,R2 andR3are put in series, the effective resistance will be
View Solution