Two resistances R and 2R are connected in parallel in an electric circuit. The thermal energy developed in R and 2R are in the ratio
(a)1:2
(b)2:1
(c )1:4
(d)4:1
The correct Answer is:B
To solve the problem of finding the ratio of thermal energy developed in two resistances R and 2R connected in parallel, we can follow these steps:
Step 1: Understand the Concept of Heat Dissipation
The thermal energy (or heat) developed in a resistor can be calculated using the formula:
H=I2RT
where H is the heat developed, I is the current flowing through the resistor, R is the resistance, and T is the time for which the current flows.
Step 2: Apply Ohm's Law
From Ohm's Law, we know that:
V=IR⇒I=VR
where V is the voltage across the resistor.
Step 3: Determine the Current through Each Resistor
For the resistors R and 2R in parallel, the voltage across both resistors is the same. Let:
- I1 be the current through resistor R
- I2 be the current through resistor 2R
Using Ohm's law:
I1=VRandI2=V2R
Step 4: Calculate Heat Developed in Each Resistor
Now, we can calculate the heat developed in each resistor:
- For resistor R:
H1=I21RT=(VR)2RT=V2R2RT=V2TR
- For resistor 2R:
H2=I22(2R)T=(V2R)2(2R)T=V24R2(2R)T=V2T2R
Step 5: Find the Ratio of Heat Developed
Now, we can find the ratio of heat developed in R and 2R:
H1H2=V2TRV2T2R=2RR=2
Thus, the ratio of thermal energy developed in R to that in 2R is:
H1:H2=2:1
Conclusion
The thermal energy developed in resistances R and 2R are in the ratio 2:1.
---
The thermal energy (or heat) developed in a resistor can be calculated using the formula:
H=I2RT
where H is the heat developed, I is the current flowing through the resistor, R is the resistance, and T is the time for which the current flows.
From Ohm's Law, we know that:
V=IR⇒I=VR
where V is the voltage across the resistor.
For the resistors R and 2R in parallel, the voltage across both resistors is the same. Let:
- I1 be the current through resistor R
- I2 be the current through resistor 2R
I1=VRandI2=V2R
Now, we can calculate the heat developed in each resistor:
- For resistor R:
H1=I21RT=(VR)2RT=V2R2RT=V2TR
H2=I22(2R)T=(V2R)2(2R)T=V24R2(2R)T=V2T2R
Now, we can find the ratio of heat developed in R and 2R:
H1H2=V2TRV2T2R=2RR=2
Thus, the ratio of thermal energy developed in R to that in 2R is:
H1:H2=2:1
The thermal energy developed in resistances R and 2R are in the ratio 2:1.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 29videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises84videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - worked out Example33videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer6videos
ELECTRIC CURRENT THROUGH GASES
Similar Questions
Knowledge Check
- Question 1 - Select One
When resistors R1andR2 are connected in a parallel electric circuit, the total resistance is 11R1+1R2. This fraction is equivalent to
AR1+R2BR1+R2R1R2CR1R2+R2R1DR1R2R1+R2
In the circuit diagram,heat produces in R, 2R and 1.5R are in the ratio of
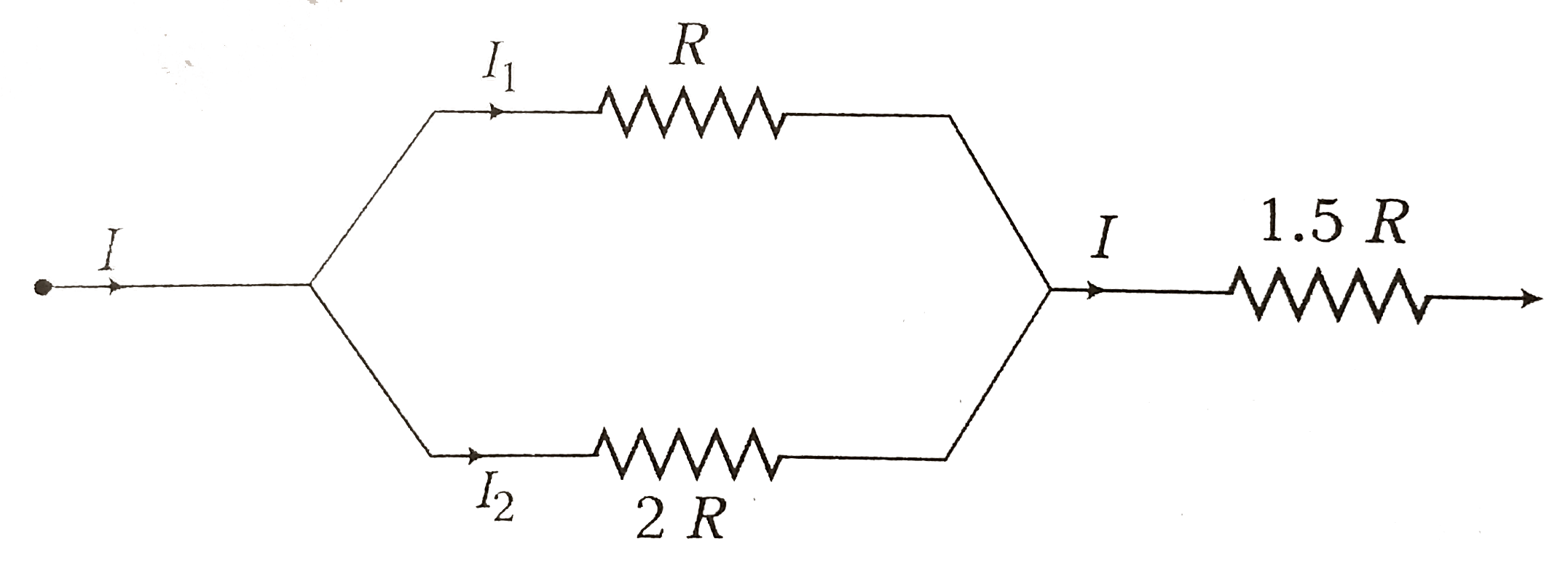 View Solution
View SolutionTwo resistors R1=400ΩandR2=20Ω are connected in parallel to a battery. If heating power developed in R1 is 25. W. find the heating power developed in R2.
View SolutionShow by a diagram how two resistors R1andR2 are joined in parallel. Obtain an expression for the total resistance of the combination.
View SolutionTwo cells of equal e.m.f. E b ut of difference internal resistance r1 and r2 are connected in parallel and the combination is connected with an external resistance R to obtain maximum power in R. find the value of R
 View Solution
View SolutionTwo unequal resistances R1andR2 ae connected across two identical batteries of emfε and internal resistance r(figure). Can the thermal energies developed in R1andR2 be equal in a given time. If yes, what will be the condition? (Figure Question)
 View Solution
View SolutionWhen two resistances R1andR2 are connected in series , they consume 12 W powers . When they are connected in parallel , they consume 50 W powers . What is the ratio of the powers of R1andR2 ?
View Solution
Two batteries of E1 internal resistance r1 & emf E2 internal resistance r2 are connected in parallel and makes a battery system. An external resistance R is connected across this system as shown in the figure.View Solution

