A capacitance C, a resistance R and an emf (ε)are connected in series at t=0.What is the maximum value of (a) the potential difference across the resistor, (b) the current in the circuit,(c )the potential difference across the capacitor, (d) the energy stored in the capacitor ,(e)the power delivered by the battery and (f) the power converted int heat.
To solve the problem step by step, we will analyze each part of the question regarding the circuit consisting of a capacitor (C), a resistor (R), and an EMF source (ε) connected in series.
1. Maximum Potential Difference Across the Resistor (V_R):
- At time t=0, the capacitor is uncharged, and it behaves like a short circuit. Therefore, the entire EMF is across the resistor.
- Formula: VR=ϵ
- Answer: The maximum potential difference across the resistor is ϵ.
2. Maximum Current in the Circuit (I_max):
- At t=0, the current is at its maximum because the capacitor has not started charging yet.
- Using Ohm's Law, the maximum current can be calculated as:
- Formula: Imax=ϵR
- Answer: The maximum current in the circuit is ϵR.
3. Maximum Potential Difference Across the Capacitor (V_C):
- As time approaches infinity, the capacitor becomes fully charged, and the potential difference across it equals the EMF of the battery.
- Formula: VC=ϵ
- Answer: The maximum potential difference across the capacitor is ϵ.
4. Energy Stored in the Capacitor (U):
- The energy stored in a capacitor when fully charged is given by the formula:
- Formula: U=12Cϵ2
- Answer: The maximum energy stored in the capacitor is 12Cϵ2.
5. Maximum Power Delivered by the Battery (P_max):
- The maximum power delivered by the battery occurs at the moment the current is maximum, which can be calculated as:
- Formula: Pmax=ϵ2R
- Answer: The maximum power delivered by the battery is ϵ2R.
6. Power Converted into Heat (P_heat):
- The power converted into heat in the resistor is equal to the power delivered by the battery at the moment of maximum current.
- Formula: Pheat=ϵ2R
- Answer: The power converted into heat is ϵ2R.
Summary of Answers:
- (a) VR=ϵ
- (b) Imax=ϵR
- (c) VC=ϵ
- (d) U=12Cϵ2
- (e) Pmax=ϵ2R
- (f) Pheat=ϵ2R
- At time t=0, the capacitor is uncharged, and it behaves like a short circuit. Therefore, the entire EMF is across the resistor.
- Formula: VR=ϵ
- Answer: The maximum potential difference across the resistor is ϵ.
- At t=0, the current is at its maximum because the capacitor has not started charging yet.
- Using Ohm's Law, the maximum current can be calculated as:
- Formula: Imax=ϵR
- Answer: The maximum current in the circuit is ϵR.
- As time approaches infinity, the capacitor becomes fully charged, and the potential difference across it equals the EMF of the battery.
- Formula: VC=ϵ
- Answer: The maximum potential difference across the capacitor is ϵ.
- The energy stored in a capacitor when fully charged is given by the formula:
- Formula: U=12Cϵ2
- Answer: The maximum energy stored in the capacitor is 12Cϵ2.
- The maximum power delivered by the battery occurs at the moment the current is maximum, which can be calculated as:
- Formula: Pmax=ϵ2R
- Answer: The maximum power delivered by the battery is ϵ2R.
- The power converted into heat in the resistor is equal to the power delivered by the battery at the moment of maximum current.
- Formula: Pheat=ϵ2R
- Answer: The power converted into heat is ϵ2R.
- (a) VR=ϵ
- (b) Imax=ϵR
- (c) VC=ϵ
- (d) U=12Cϵ2
- (e) Pmax=ϵ2R
- (f) Pheat=ϵ2R
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer17videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 29videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer6videos
ELECTRIC CURRENT THROUGH GASES
Similar Questions
In the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
View SolutionIn the given circuit, calculate -

(a) the total resistance of the circuit,
(b) the current through the circuit, and
(c) the potential differences across R1andR2View SolutionThere identical point masses, each of mass 1 kg lie in the xy-plane at points (0, 0), (0, 0.2 m) and (0, 2m, 0). The net gravitational force on the mass at the origin is:
View Solutionin a series LCR circuit, what is the phase difference between VLandVC where VL is the potential difference across the inductor and VC is the potential difference across the capacitor?
View SolutionIn the circuit the potential difference across the capacitor is 10V. Each resistance is of 3Ω The cell is ideal. The emf of the cell is
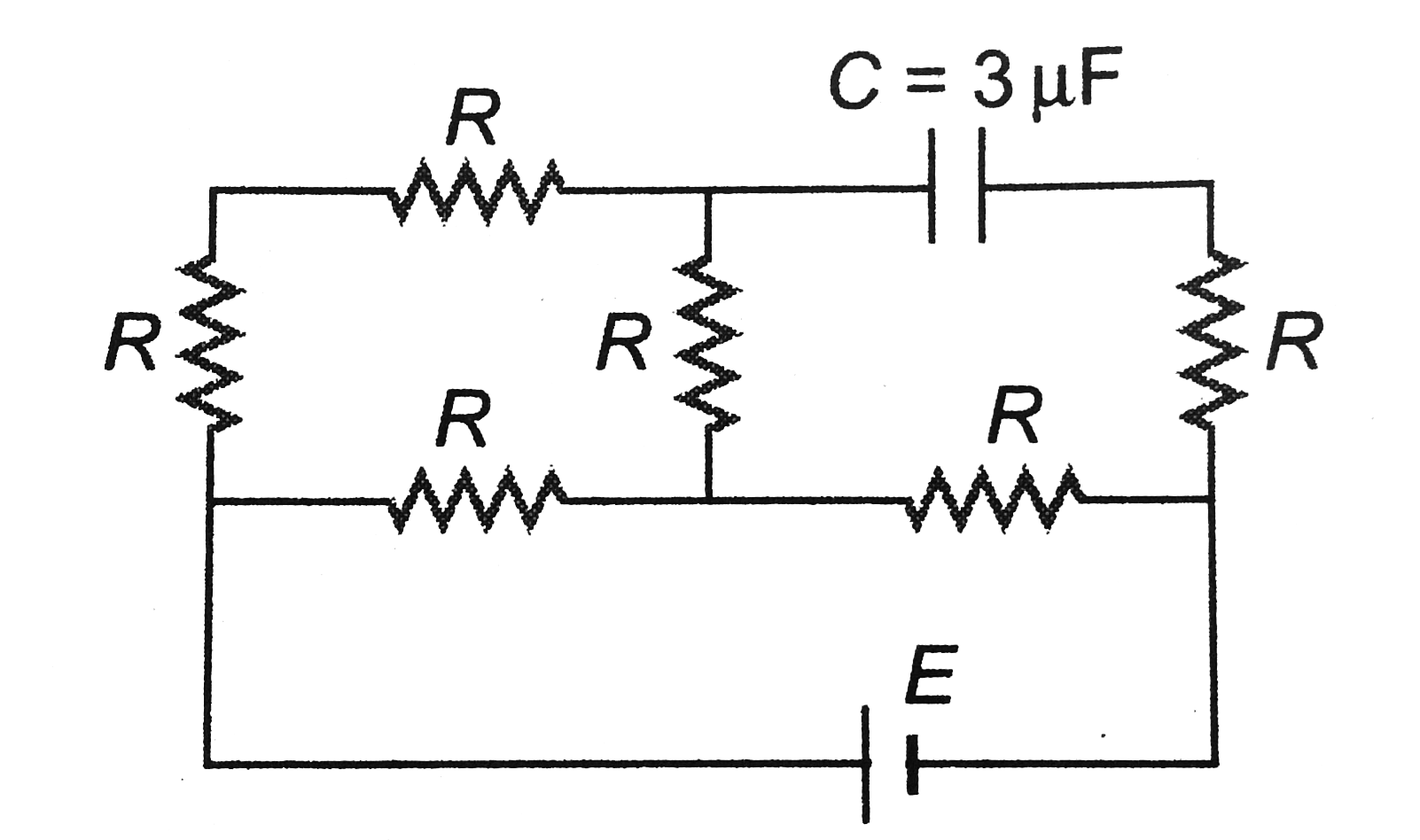 View Solution
View SolutionIf A is connerted with D and B is connected with C find the potential difference a across each capacitor and the final charge in each capacitor.
View SolutionAn AC source is connected with a resistance ( R) and an unchanged capacitance C, in series. The potential difference across the resistor is in phase with the initial potential difference across the capacitor for the first time at the instant (assume that at t =0 , emf is zero)
View SolutionTwo capacitors of capacitances 20.0pF and 50.0pF are connected in series with a 6.00V bettery . Find (a )the potential difference across each capacitor and (b) the energy stored in each capacitor .
View SolutionTwo capacitances of capacity C1and C2 are connected in series and potential difference V is applied across it. Then the potential difference across C1 will be
View SolutionAn electric lamp of resistance 2Ω and a conductor of resistance 4Ωare connected to a
6V Battery as shown in the circuit. Calculate:
(a) the totak resistance of the circuit,
(b) the current through the circuit,
(c) the potential difference across the (i) electric lamp
and (ii) conductor, and
(d) power of the lamp.
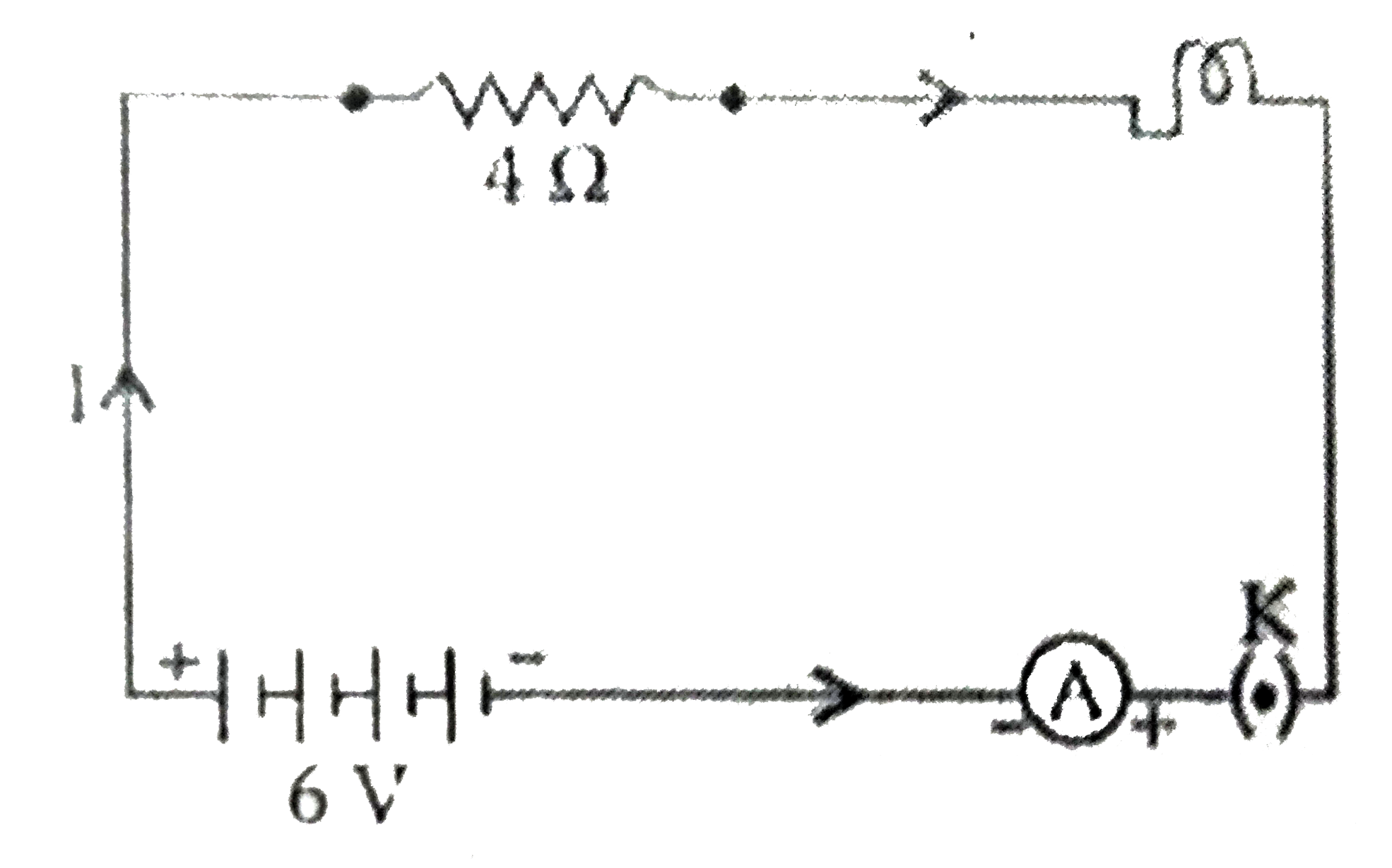 View Solution
View Solution

