The magnetic field due to a long straight wire has been derived in terms of μ0,i and d. Express this in terms of var epsilon_0, c, I, and d.
To express the magnetic field B due to a long straight wire in terms of ϵ0, c, I, and d, we start from the known expression for the magnetic field:
1. Starting Expression: The magnetic field B at a distance d from a long straight current-carrying wire is given by:
B=μ0I2πd
2. Relate μ0 to ϵ0 and c: We know that the speed of light c is related to the permeability μ0 and permittivity ϵ0 of free space by the equation:
c=1√μ0ϵ0
Squaring both sides gives:
c2=1μ0ϵ0
Rearranging this, we find:
μ0=1c2ϵ0
3. Substituting μ0 into the Magnetic Field Equation: Now we substitute μ0 back into the expression for B:
B=1c2ϵ0I2πd
4. Simplifying the Expression: This simplifies to:
B=I2πϵ0c2d
5. Final Expression: Thus, the magnetic field B in terms of ϵ0, c, I, and d is given by:
B=I2πϵ0c2d
B=μ0I2πd
c=1√μ0ϵ0
Squaring both sides gives:
c2=1μ0ϵ0
Rearranging this, we find:
μ0=1c2ϵ0
B=1c2ϵ0I2πd
B=I2πϵ0c2d
B=I2πϵ0c2d
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
Dimension of resistance R in terms of μ0&ε0 are
View SolutionDimension of resistance R in terms of μ0&ε0 are
View SolutionWhich of the following correctly describes the magnetic field near a long straight wire?
(a) The field consists of straight lines perpendicular to the wire.
(b) The field consists of straight lines parallel to the wire.
(c) The field consists of radial lines originating from the wire.
(d) The field consists of concentric circles centered on the wire.
View SolutionB0 is the magnetic field at point P for a given straight wire as shown in figure. If this wirre is bent into a circular loop, then magnetic field at the centre of loop is
_PHY_E06_130_Q01.png)
View SolutionThe magnetic field strength at a point P distant r due to an infinite straight wire carrying a current i is as shown in the figure
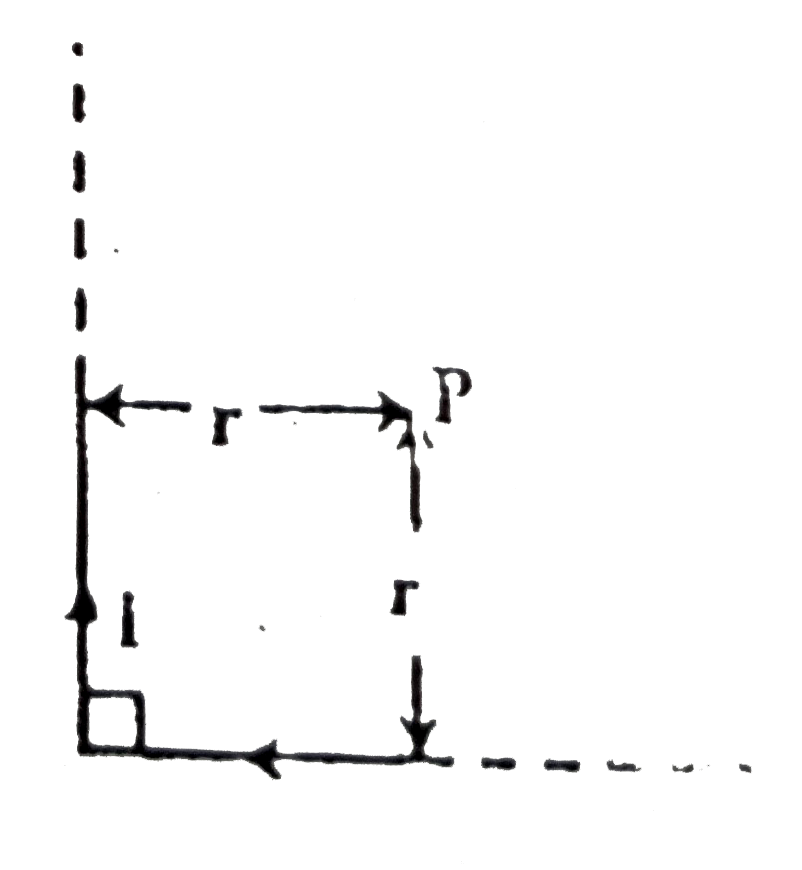
View SolutionA long conducting wire carrying a current I is bent at 120∘( see figure). The magnetic field B at a point P on the right bisector of bending angle at a distance d from the bend is
(μ0 is the permeability of free space)

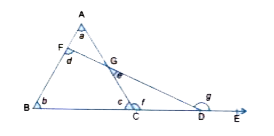
View SolutionUse the given figure to express :
(i) a in terms of b and f,
(ii) e in terms of f and g,
(iii) d in terms of a and e,
(iv) c in terms of e and g.
View SolutionThe magnetic field at a distance r from a long wire carryimg current I is 0.4 T. The magnetic field at a distance 2r is
View SolutionA very long bar magnet is placed with its north pole coinciding with the centre of a circular loop carrying an electric current. i. The magnetic field due to the magnet at a point on the periphery of the wire is B. The radius of the loop is a. The force on the wire is
View SolutionAccording to Biot-Savarat's law, magentic field due to a straight current carrying wire at a point at a distance r form it is given by
B=μ0I4πr(sinϕ1+sinϕ2)
The direction of magnetic field being perpendicular to the plane containing the wire and the point.

Figure, shows a closed loop AOCBA in which current I is flowing as shown. Given OA=OB=OC=a. Find the magnetic field at point B due to this loop.

View Solution
