Quite often, connecting wires carrying currents in opposite directions are twisted together in using electrical appliances. Explain how it avoids unwanted magnetic fields.
To explain how twisting wires carrying currents in opposite directions avoids unwanted magnetic fields, we can break down the solution into several steps:
1. Understanding Current Direction:
- Consider two wires: Wire 1 carries current in one direction (let's say upwards), and Wire 2 carries current in the opposite direction (downwards).
2. Magnetic Field Generation:
- According to Ampère's circuital law, a current-carrying wire generates a magnetic field around it. The direction of this magnetic field can be determined using the right-hand thumb rule. For Wire 1, the magnetic field will be directed out of the plane (towards you), and for Wire 2, it will be directed into the plane (away from you).
3. Analyzing Magnetic Fields:
- When we analyze the magnetic fields produced by both wires:
- For Wire 1, the magnetic field lines are directed out of the plane.
- For Wire 2, the magnetic field lines are directed into the plane.
- If we consider a point equidistant from both wires, the magnetic fields produced by each wire will oppose each other.
4. Resultant Magnetic Field:
- Since the magnetic fields from the two wires are equal in magnitude but opposite in direction, they will cancel each other out. This means that at any point in space between the two wires, the net magnetic field will be zero.
5. Long Length of Wires:
- This cancellation effect holds true along the entire length of the twisted wires. Therefore, when the wires are twisted together, the net magnetic field produced by the two wires remains zero, effectively avoiding any unwanted magnetic fields in the surrounding area.
6. Conclusion:
- By twisting the wires carrying currents in opposite directions, we ensure that their magnetic fields cancel each other out, leading to a net magnetic field of zero. This is particularly useful in electrical appliances where unwanted magnetic fields can cause interference or affect the operation of other components.
- Consider two wires: Wire 1 carries current in one direction (let's say upwards), and Wire 2 carries current in the opposite direction (downwards).
- According to Ampère's circuital law, a current-carrying wire generates a magnetic field around it. The direction of this magnetic field can be determined using the right-hand thumb rule. For Wire 1, the magnetic field will be directed out of the plane (towards you), and for Wire 2, it will be directed into the plane (away from you).
- When we analyze the magnetic fields produced by both wires:
- For Wire 1, the magnetic field lines are directed out of the plane.
- For Wire 2, the magnetic field lines are directed into the plane.
- If we consider a point equidistant from both wires, the magnetic fields produced by each wire will oppose each other.
- Since the magnetic fields from the two wires are equal in magnitude but opposite in direction, they will cancel each other out. This means that at any point in space between the two wires, the net magnetic field will be zero.
- This cancellation effect holds true along the entire length of the twisted wires. Therefore, when the wires are twisted together, the net magnetic field produced by the two wires remains zero, effectively avoiding any unwanted magnetic fields in the surrounding area.
- By twisting the wires carrying currents in opposite directions, we ensure that their magnetic fields cancel each other out, leading to a net magnetic field of zero. This is particularly useful in electrical appliances where unwanted magnetic fields can cause interference or affect the operation of other components.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
STATEMENT-1: In electric circuits, wires carrying currents in opposite directions are often twisted together. because
STATEMENT-2: The magnetic field in the surrounding space of a twisted wire system is not precisely zero because the wires are not in the same location in space.
View SolutionHow does use of a fuse-wire protect electrical appliances ?
View SolutionTwo long wires carrying same currents in opposite directions are placed at separation D as shown.Predict variation of magnetic field as one moves from the point O and A
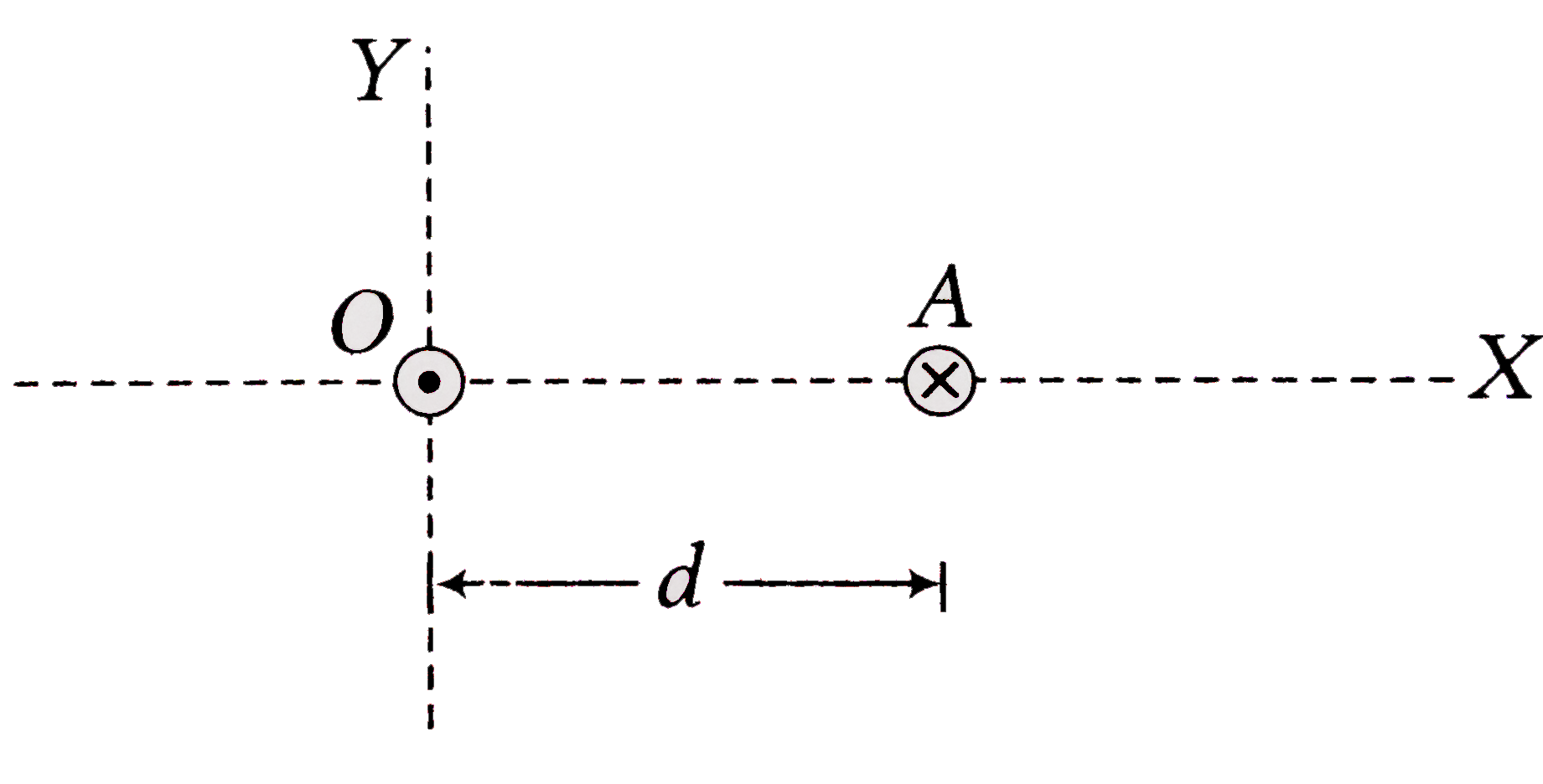
View SolutionThe two long, straight wires carrying electric currents in opposite directions. The separation between the wires is 5.0 cm. Find the magnetic field at a point P midway between the wires.
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionA current carrying circular coil is bent so as to convert it into a double loop, both the loops being concentric and are carrying current in the same direction. If B is the initial magnetic field at the centre, the final magnetic field at the centre will be
View SolutionA conducting wire carrying current I is shown in the figure. The magnitude of magnetic field at the point P will be

View SolutionThe magnetic field midway between two parallel current carrying wires, carrying currents I and 2i in same direction is B. If the current in the wire with current I is switched off, the magnetic field will become
View SolutionTwo parallel wires P and Q placed at a separation
d=6cm carry electric currents i_1= 5A and i_2= 2A in <br> opposite directions as shown in figure. Find the<br> point on the line PQ where the resultant magnetic field
is zero.

View SolutionIn fig. two long parallel wires carry equal currents in opposite directions. Point O is situated midway between the wires and X−Y plane contains the two wires and the position Z-axis comes normally out of the plane of paper. The magnetic field B at O is non-zero along
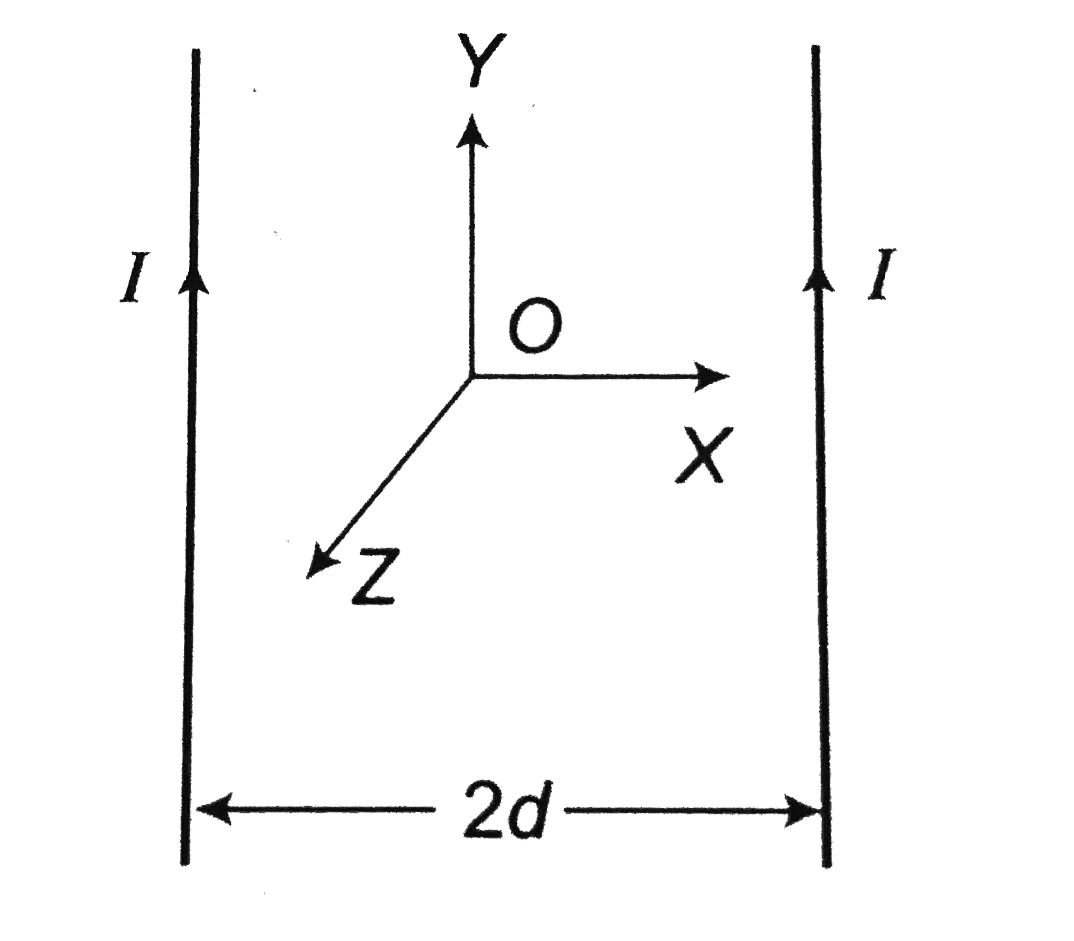
View Solution
