The magnetic field inside a tightly wound, long solenoid is B= (mu_0)ni. It suggests that the field does not depend on the total length of the solenoid, and hence if we add more loops at the ends of a solenoid the field should not increase. Explain qualitatively why the extra added loops do not have a considerable effect on the field inside the solenoid.
Step by step video & image solution for The magnetic field inside a tightly wound, long solenoid is B= (mu_0)ni. It suggests that the field does not depend on the total length of the solenoid, and hence if we add more loops at the ends of a solenoid the field should not increase. Explain qualitatively why the extra added loops do not have a considerable effect on the field inside the solenoid. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:exercise
Explore 60 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC PROPERTIES OF MATTERBook:HC VERMA ENGLISHChapter:MAGNETIC PROPERTIES OF MATTERExercise:Short Answer
Explore 6 Videos
Similar Questions
Knowledge Check
Current flowing through a long solenoid is varied. Then, magnetic flux density of the magnetic field inside it varies :
Ainversely with IBinversely withI2Cdirectly with IDdirectly with I2
The magnetic field inside a toroidal solenoid of radius R is B. If the current through it is doubled and its radius is also doubled, keeping the number of turns same, the magnetic field produced by it will be
View SolutionThe magnetic field at a point on the axis of a long solenoid having 5 turns per cm length when a current of 0.8 A flows through it is
View SolutionA thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.

A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
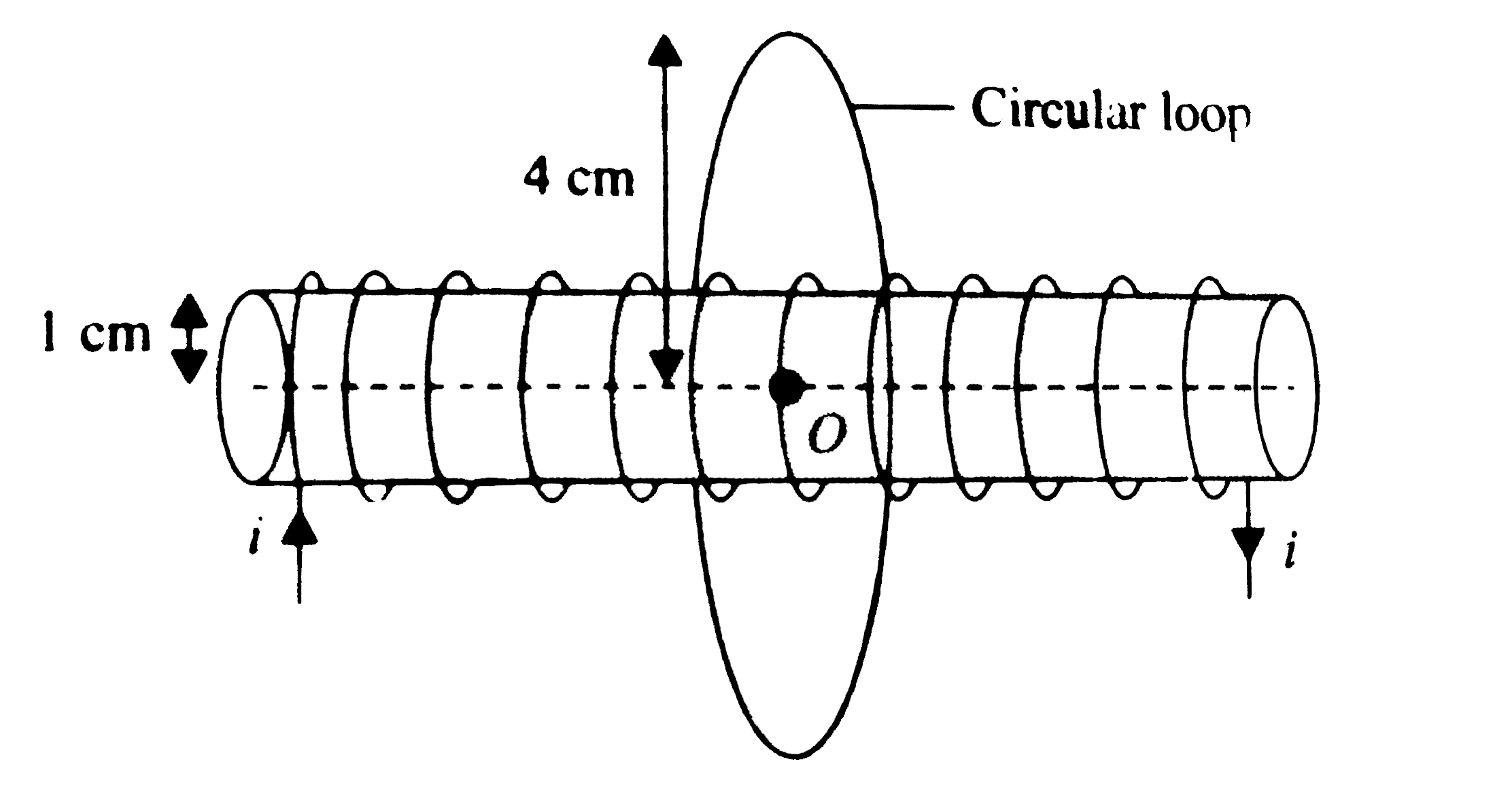
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magentic flux through the loop due to external magnetic field will be
I is the current in the loop
a1 is the radius of solendoid and a1=1cm (given)
a2 is the radius of circular loop and a2=4cm (given)
i is hte current in the solenoid
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
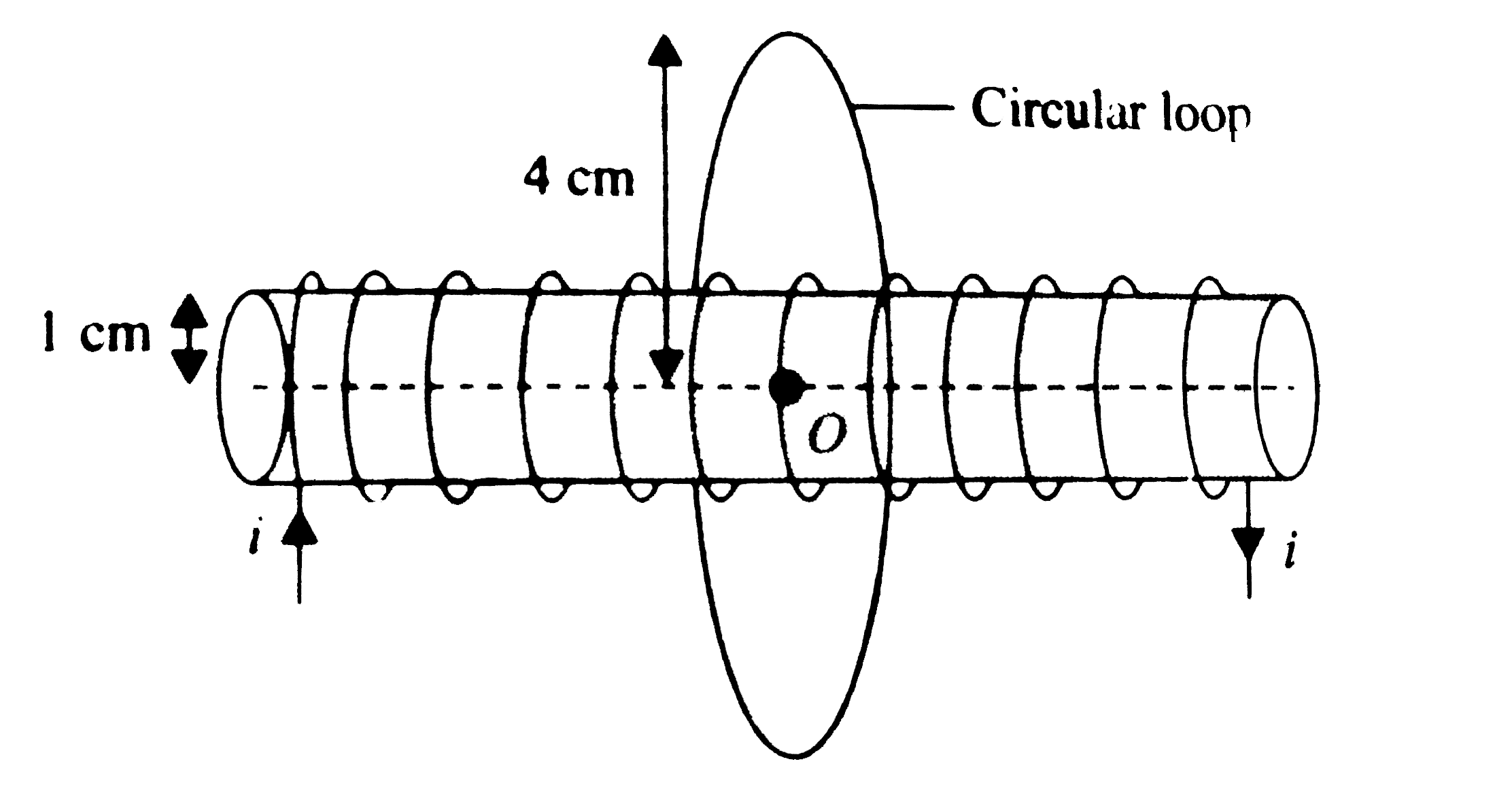
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
Magnitude of induced current that appears in the circular loop is
View SolutionA wire is wound on a long rod of material of relative permeability μr=4000 to make a solenoid. If the current through the wire is 5 A and number of turns per unit length is 1000 per metre, then the magnetic field inside the solenoid is
View Solution
