Two long, straight wires, each carrying a current of 5A, are placed along the x and y axes respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1m, 1m), (b) (-1m, 1m), (c) (-1m, -1m) and (d) (1m, -1m).
To solve the problem of finding the magnetic fields at the specified points due to two long straight wires carrying currents, we will follow these steps:
Step 1: Understand the Configuration
We have two long straight wires:
- Wire 1 along the x-axis carrying a current of 5 A in the positive x-direction.
- Wire 2 along the y-axis carrying a current of 5 A in the positive y-direction.
Step 2: Use the Formula for Magnetic Field
The magnetic field B due to a long straight wire at a distance r from the wire is given by the formula:
B=μ0I2πr
where:
- μ0=4π×10−7T m/A (permeability of free space),
- I is the current in amperes,
- r is the distance from the wire to the point of interest.
Step 3: Analyze Each Point
We will calculate the magnetic field at each of the four points given: (1, 1), (-1, 1), (-1, -1), and (1, -1).
Point A: (1, 1)
- Distance from the x-axis wire = 1 m (vertical distance).
- Distance from the y-axis wire = 1 m (horizontal distance).
Magnetic field due to wire along x-axis (B_x):
- Direction: Out of the page (using the right-hand rule).
Bx=μ0⋅52π⋅1=4π×10−7⋅52π=10×10−7T=1×10−6T
Magnetic field due to wire along y-axis (B_y):
- Direction: Into the page.
By=μ0⋅52π⋅1=1×10−6T
Net Magnetic Field at Point A:
- Since Bx and By are equal in magnitude but opposite in direction, they cancel each other out.
Bnet=Bx−By=0T
Point B: (-1, 1)
- Distance from the x-axis wire = 1 m.
- Distance from the y-axis wire = 1 m.
Magnetic field due to wire along x-axis (B_x):
- Direction: Out of the page.
Bx=1×10−6T
Magnetic field due to wire along y-axis (B_y):
- Direction: Out of the page.
By=1×10−6T
Net Magnetic Field at Point B:
- Both fields are in the same direction (out of the page).
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T
Point C: (-1, -1)
- Distance from the x-axis wire = 1 m.
- Distance from the y-axis wire = 1 m.
Magnetic field due to wire along x-axis (B_x):
- Direction: Into the page.
Bx=1×10−6T
Magnetic field due to wire along y-axis (B_y):
- Direction: Out of the page.
By=1×10−6T
Net Magnetic Field at Point C:
- Since Bx and By are equal in magnitude but opposite in direction, they cancel each other out.
Bnet=Bx−By=0T
Point D: (1, -1)
- Distance from the x-axis wire = 1 m.
- Distance from the y-axis wire = 1 m.
Magnetic field due to wire along x-axis (B_x):
- Direction: Into the page.
Bx=1×10−6T
Magnetic field due to wire along y-axis (B_y):
- Direction: Out of the page.
By=1×10−6T
Net Magnetic Field at Point D:
- Both fields are in the same direction (into the page).
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T
Summary of Results
- Point A (1, 1): B=0T
- Point B (-1, 1): B=2×10−6T (out of the page)
- Point C (-1, -1): B=0T
- Point D (1, -1): B=2×10−6T (into the page)
We have two long straight wires:
- Wire 1 along the x-axis carrying a current of 5 A in the positive x-direction.
- Wire 2 along the y-axis carrying a current of 5 A in the positive y-direction.
The magnetic field B due to a long straight wire at a distance r from the wire is given by the formula:
B=μ0I2πr
where:
- μ0=4π×10−7T m/A (permeability of free space),
- I is the current in amperes,
- r is the distance from the wire to the point of interest.
We will calculate the magnetic field at each of the four points given: (1, 1), (-1, 1), (-1, -1), and (1, -1).
- Distance from the x-axis wire = 1 m (vertical distance).
- Distance from the y-axis wire = 1 m (horizontal distance).
- Direction: Out of the page (using the right-hand rule).
Bx=μ0⋅52π⋅1=4π×10−7⋅52π=10×10−7T=1×10−6T
- Direction: Into the page.
By=μ0⋅52π⋅1=1×10−6T
- Since Bx and By are equal in magnitude but opposite in direction, they cancel each other out.
Bnet=Bx−By=0T
- Distance from the x-axis wire = 1 m.
- Distance from the y-axis wire = 1 m.
- Direction: Out of the page.
Bx=1×10−6T
- Direction: Out of the page.
By=1×10−6T
- Both fields are in the same direction (out of the page).
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T
- Distance from the x-axis wire = 1 m.
- Distance from the y-axis wire = 1 m.
- Direction: Into the page.
Bx=1×10−6T
- Direction: Out of the page.
By=1×10−6T
- Since Bx and By are equal in magnitude but opposite in direction, they cancel each other out.
Bnet=Bx−By=0T
- Distance from the x-axis wire = 1 m.
- Distance from the y-axis wire = 1 m.
- Direction: Into the page.
Bx=1×10−6T
- Direction: Out of the page.
By=1×10−6T
- Both fields are in the same direction (into the page).
Bnet=Bx+By=1×10−6+1×10−6=2×10−6T
- Point A (1, 1): B=0T
- Point B (-1, 1): B=2×10−6T (out of the page)
- Point C (-1, -1): B=0T
- Point D (1, -1): B=2×10−6T (into the page)
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A current of 10A is established in a long wire along the positive z-axis. Find the magnetic field (vec B) at the point (1m , 0 , 0).
View SolutionThree semi - inifinte wires, each carrying a current of 1 A are placed on each of the coordinate axes with their ends at the origin, as shown in the figure. The magnetic induction at point P(−2m,0,0) is
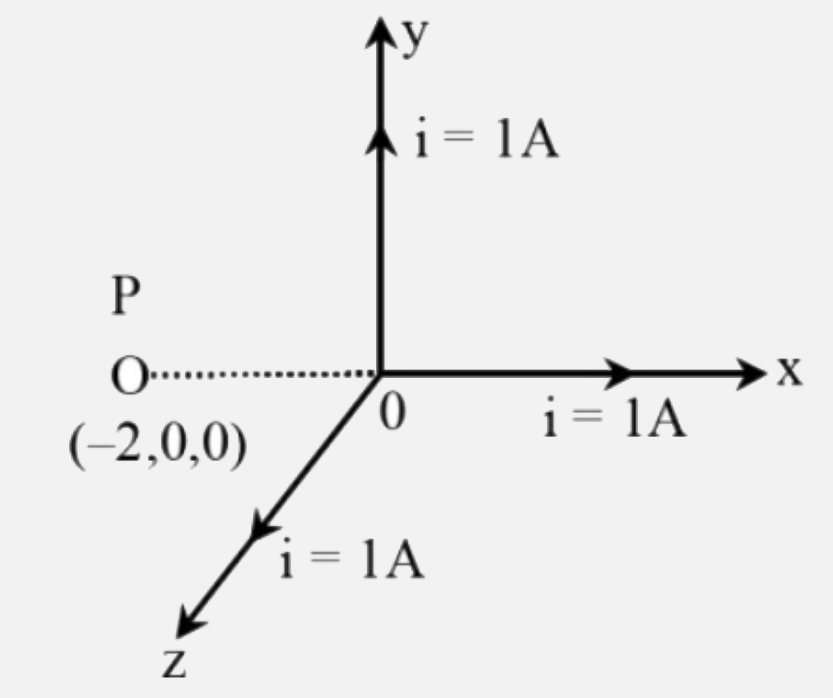
View Solution
Knowledge Check
A straight wire having mass of 1.2 kg and length of 1m carries a current of 5 A. If the wire is suspended in mid-air by a uniform horizontal magnetic field, then the magnitude of field is
A0.65TB1.53TC2.4TD3.2T
Two long straight conductors with current I1 and I2 are placed along X and Y axes. The equation of locus of points of zero magnetic induction is :
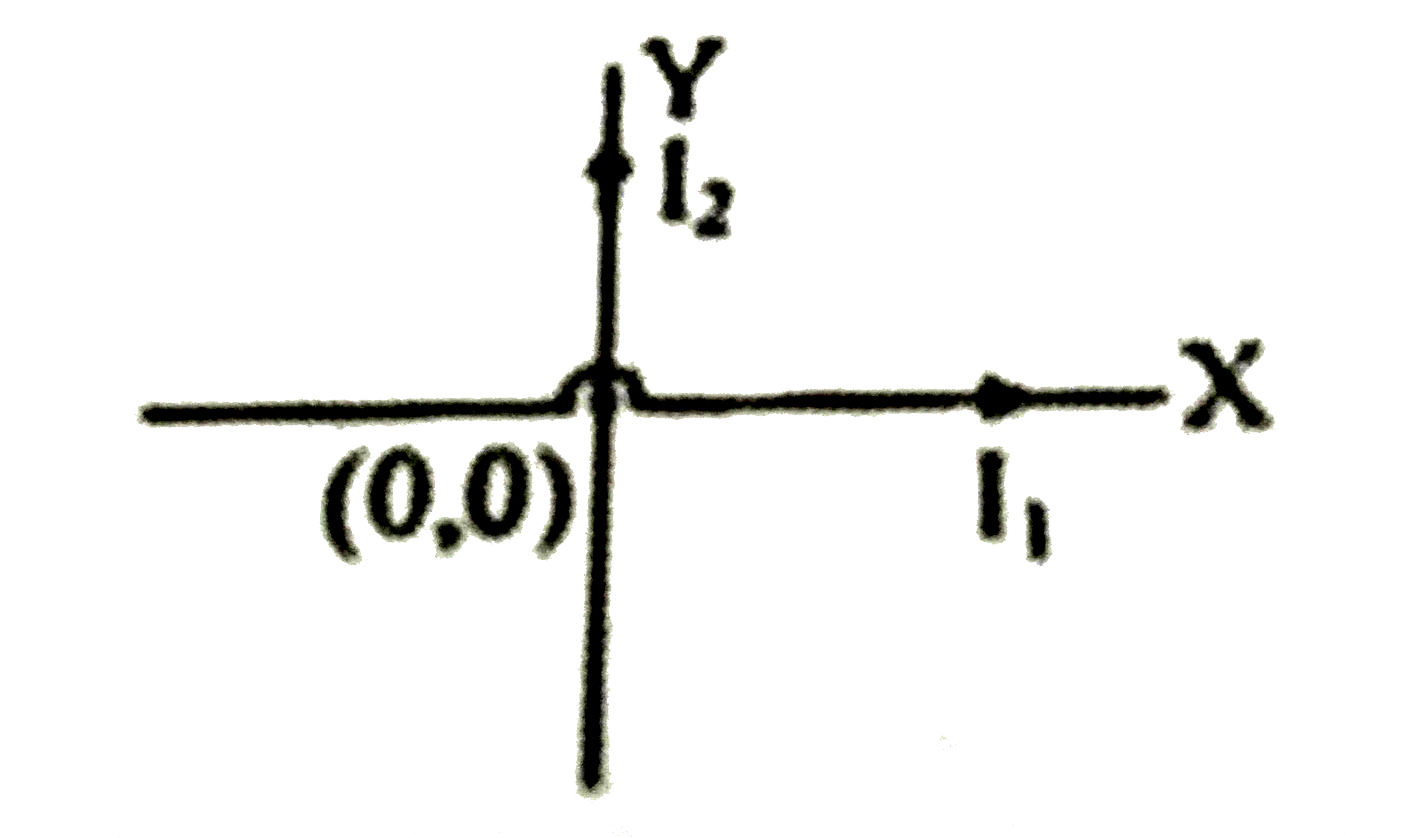
View SolutionThree infinitely long wires, each carrying a current 1A, are placed such that one end of each wire is at the origin, and, one of these wires is along x-axis, the other along y-axis and the third along z-axis. Magnetic induction at point (-2 m, 0, 0) due to the system of these wires can be expressed as
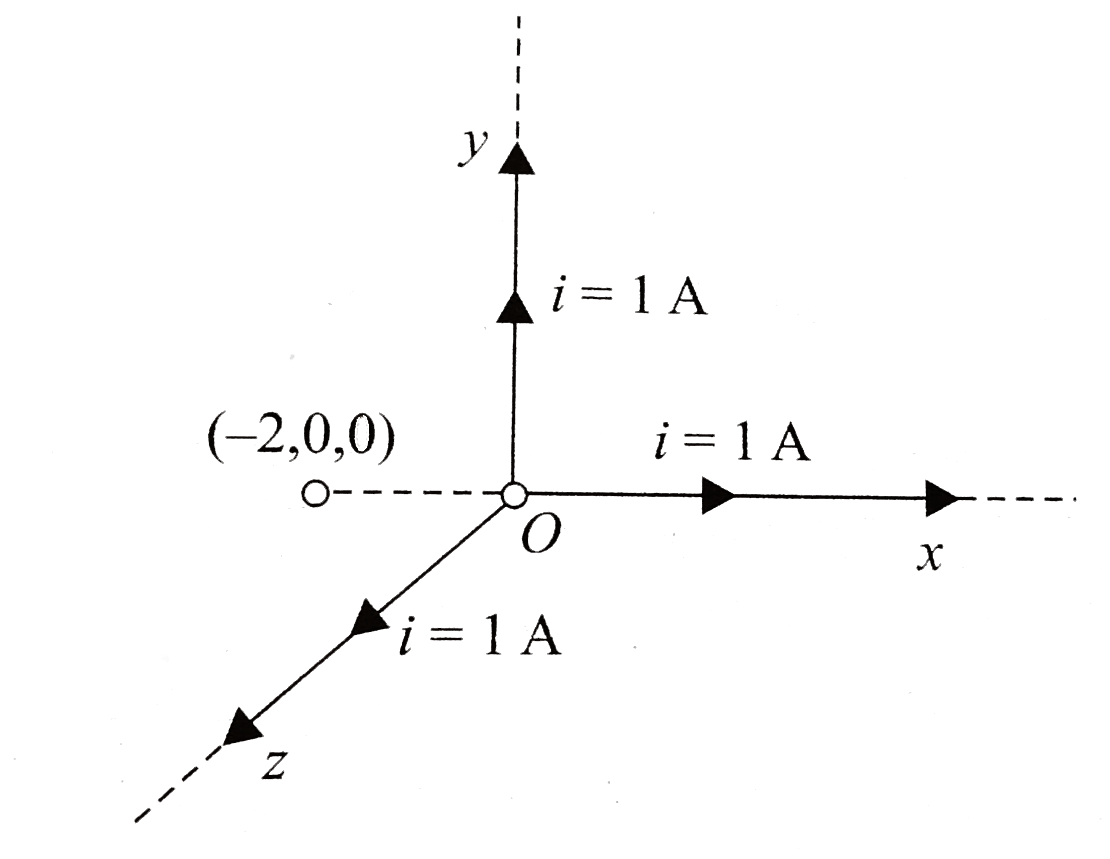
View SolutionIf a thin uniform wire of length 1m is bent into an equilateral triangle and carries a current of √3A in anticlockwise direction, find the net magnetic induction at the centroid
View SolutionMoment of a force of magnitude 10 N acting along positive y-direction at point (2m,0,0) about the point (0,1m,0) in N-m is
View SolutionAs charge q=1μC is placed at point (1m,2m,4m). Find the electric field at point P(0,−4m,3m)
View SolutionThe electric potential V at any point x,y,z (all in metre) in space is given by V=4x2 volt. The electric field at the point (1m,0,2m) is ……………Vm.
View SolutionProve that a point can be found which is at the same distance from each of the four points :(am1,am1),(am2,am2),(am3,am3)and(am1m2m3,am1m2m3)
View Solution
