The force on a north pole, →F=m→B, is parallel to the field m→B, is parallel to the field vetB. Does it contradict our earlier knowledge that a magnetic field can exert forces only perpendicular to itself?
Step by step video & image solution for The force on a north pole, vec F = m vec B, is parallel to the field mvec B, is parallel to the field vet B. Does it contradict our earlier knowledge that a magnetic field can exert forces only perpendicular to itself? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PERMANENT MAGNETSBook:HC VERMA ENGLISHChapter:PERMANENT MAGNETSExercise:Exercise
Explore 25 Videos
- OPTICAL INSTRUMENTSBook:HC VERMA ENGLISHChapter:OPTICAL INSTRUMENTSExercise:Question for short Answer
Explore 12 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBook:HC VERMA ENGLISHChapter:PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYExercise:question for short answer
Explore 13 Videos
Similar Questions
Two bar magnets are placed close to each other with their opposite poles facing each other. In absence of other forces, the magnets are pulled towards each other and their kinetc energy increases. Does it contradict our earlier knowledge that magnetic forces cannot do any work and hence cannot increase kinetic energy of a system?
View SolutionThe net charge in a current carrying wire is zero. Them, why does a magnetic field exert a force on it?
View SolutionAn electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
View SolutionInitially plane of coil is parallel to the uniform magnetic field B. In time Δt it makes to perpendicular to the magnetic field, then charge flows in Δt depends on this time as -
View SolutionA charge q moves region in a electric field E and the magnetic field B both exist, then the force on its is
View SolutionThe force on a charged particle moving in a magnetic field can be computed as the vector sum of the force due to each separate component of the magnetic field. As an example, a particle with charge q is moving with speed v in the -y direction. It is moving in a uniform magnetic field →B=Bxˆi+Byˆj+Bzˆk.
a. What are the components of the force →F exerted on the particle by the magnetic field?
b. If q>0, what must the signs of the components of →B be if the components of →F are all non-negative?
c. If q<0andBx=By=Bz>0, find the direction and magnitude of →F in terms of |q|, v and Bx.
View SolutionAn alpha particle moving with the velocity →v=uˆi+ˆj ,in a uniform magnetic field →B=Bˆk . Magnetic force on alpha particle is
View SolutionLet →a,→band→c be three units vectors such that 2→a+4→b+5→c=0. Then which of the following statement is true? a. →a is parallel to →b b. →a is perpendicular to →b c. →a is neither parallel nor perpendicular to →b d. none of these
View SolutionA velocity filter uses the properties of electric and magnetic field to select particles that are moving with a specifice velocity. Charged particles with varying speeds are directed into the filter as shown. The filter consistt of an electric field E and a magnetic field B, each of constant magnitude, directed perpendicular to each other as shown, The charge particles will experience a force due to electric field given by F = qE. If positively charged particles are used, this force is towards right.
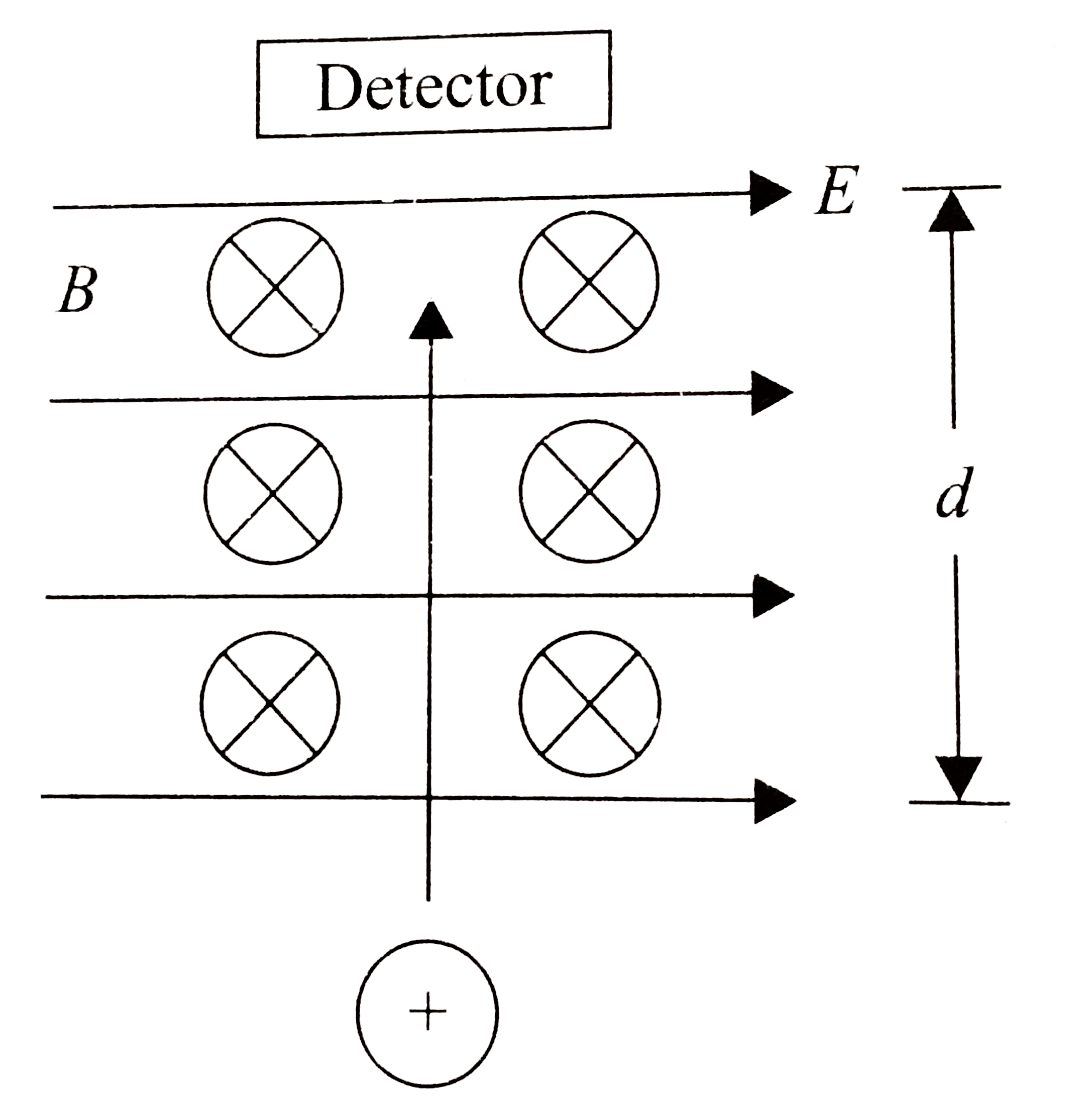
The moving particle will also experience a force due to magnetic field given by F=qvB. When forces due to the two fields are of equal magnitude, the net force on the particle will be zero, the particle will pass through centre with its path unaltered. The electric and magnetic fields can be adjusted t choose the specific velocity to be filtered. The efect of gravity can be neglected.
The electric and magnetic fields are adjusted to detect particles with positive charge q of certain speed v0. which of the following expressions is equal to this speed?
View SolutionA bar magnet of magnetic moment →M is placed in a magnetic field of induction →B . The torque exerted on it is
View Solution
