A conducting loop of face area A and resistance R is plaed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
To solve the problem of finding the charge that flows through a conducting loop when it is withdrawn from a magnetic field, we can follow these steps:
Step 1: Understanding Magnetic Flux
The magnetic flux (Φ) through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal (perpendicular) to the surface of the loop.
Since the loop is placed perpendicular to the magnetic field, θ=0 degrees. Therefore, cos(0)=1, and the magnetic flux simplifies to:
Φ=B⋅A
Step 2: Change in Magnetic Flux
When the loop is completely withdrawn from the magnetic field, the magnetic flux through the loop becomes zero. The change in magnetic flux (ΔΦ) is:
ΔΦ=Φfinal−Φinitial=0−(B⋅A)=−B⋅A
Step 3: Induced EMF
According to Faraday's law of electromagnetic induction, the induced electromotive force (emf, E) in the loop is given by the rate of change of magnetic flux:
E=−dΦdt
Assuming the loop is withdrawn in a time interval t, we can express the induced emf as:
E=−ΔΦΔt=−−B⋅At=B⋅At
Step 4: Current through the Loop
Using Ohm's law, the current (I) flowing through the loop can be calculated as:
I=ER
Substituting the expression for E:
I=B⋅AR⋅t
Step 5: Charge Flowing through the Wire
The total charge (Q) that flows through any cross-section of the wire during the time t can be calculated using the relationship:
Q=I⋅t
Substituting the expression for I:
Q=(B⋅AR⋅t)⋅t=B⋅AR
Final Answer
Thus, the charge that flows through any cross-section of the wire when the loop is withdrawn from the magnetic field is:
Q=B⋅AR
---
The magnetic flux (Φ) through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
where:
- B is the magnetic field strength,
- A is the area of the loop,
- θ is the angle between the magnetic field and the normal (perpendicular) to the surface of the loop.
Φ=B⋅A
When the loop is completely withdrawn from the magnetic field, the magnetic flux through the loop becomes zero. The change in magnetic flux (ΔΦ) is:
ΔΦ=Φfinal−Φinitial=0−(B⋅A)=−B⋅A
According to Faraday's law of electromagnetic induction, the induced electromotive force (emf, E) in the loop is given by the rate of change of magnetic flux:
E=−dΦdt
Assuming the loop is withdrawn in a time interval t, we can express the induced emf as:
E=−ΔΦΔt=−−B⋅At=B⋅At
Using Ohm's law, the current (I) flowing through the loop can be calculated as:
I=ER
Substituting the expression for E:
I=B⋅AR⋅t
The total charge (Q) that flows through any cross-section of the wire during the time t can be calculated using the relationship:
Q=I⋅t
Substituting the expression for I:
Q=(B⋅AR⋅t)⋅t=B⋅AR
Thus, the charge that flows through any cross-section of the wire when the loop is withdrawn from the magnetic field is:
Q=B⋅AR
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
A conducintg circular loop having a redius of 5.0cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced In the loop during this time.
View SolutionA uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
Aπ2r4B402τRBπ2r4B202τRCπ2r4B20RτDπ2r4B20τR - Question 2 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A uniform circular loop of radius a and resistance R palced perpendicular to a uniform magnetic field B. One half of the loop is rotated about the diameter with angular velocity ω as shown in Fig. Then, the current in the loop is
 View Solution
View SolutionA conducting metal circular-wire-loop of radius r is placed perpendicular to a magnetic field which varies with time as B=B0e−t/τ, where B0andτ are constants, at time = 0. If the resistance of the loop is R then the heat generated in the loop after a long time (t→∞) is :
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.
 View Solution
View SolutionA conducting circular loop made of a thin wire, has area 3.5×10−3m2 and resistance 10Ω. It is placed perpendicular to a time dependent magnetic field B(t)=(0.4T)sin(50πt). The field is uniform in space. Then the net charge flowing through the loop during t=0 s and t=10 ms is close to :
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is a constant and t is time. The induced current flowing through loop is
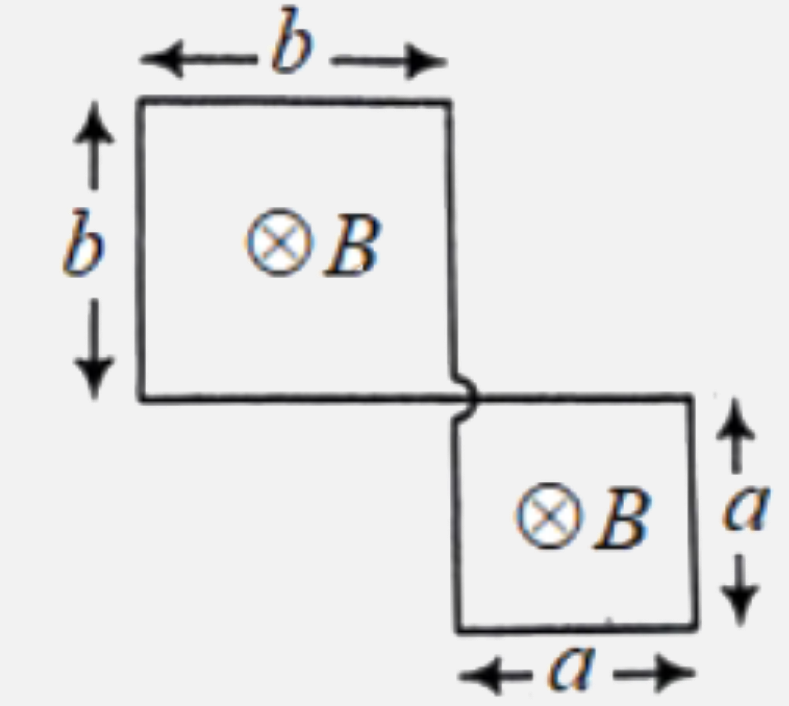 View Solution
View SolutionA conducting loop (as shown) has total resistance R. A uniform magnetic field B=γt is applied perpendicular to plane of the loop where γ is constant and t is time. The induced current flowing through loop is
 View Solution
View Solution

