A conducting loop confined in a plane is rotated in its own plane with some angular velocity.A uniform and constant magnetic field exist in the region.Find the current induced in the loop.
To solve the problem of finding the induced current in a conducting loop that is rotated in its own plane within a uniform and constant magnetic field, we can follow these steps:
1. Understand the Situation:
- We have a conducting loop that is rotating in its own plane with some angular velocity.
- There is a uniform and constant magnetic field present in the region.
2. Identify the Magnetic Flux:
- The magnetic flux (Φ) through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
- Where:
- B is the magnetic field strength.
- A is the area of the loop.
- θ is the angle between the magnetic field and the normal to the surface of the loop.
3. Analyze the Rotation:
- As the loop rotates in its own plane, the angle θ changes with time. However, since the magnetic field is uniform and constant, the magnetic field B does not change.
4. Determine the Change in Flux:
- The change in magnetic flux (ΔΦ) over time can be expressed as:
dΦdt=B⋅dAdt⋅cos(θ)+B⋅A⋅d(cos(θ))dt
- However, since the area A of the loop does not change and the magnetic field B is constant, the only term that could contribute to a change in flux is the term involving θ.
5. Evaluate the Induced EMF:
- According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF, ε) in the loop is given by:
ε=−dΦdt
- If the magnetic flux does not change (as established earlier), then:
ε=0
6. Calculate the Induced Current:
- The induced current I can be calculated using Ohm's law:
I=εR
- Since the induced EMF ε=0, we have:
I=0R=0
Final Answer:
The induced current in the loop is 0.
- We have a conducting loop that is rotating in its own plane with some angular velocity.
- There is a uniform and constant magnetic field present in the region.
- The magnetic flux (Φ) through the loop is given by the formula:
Φ=B⋅A⋅cos(θ)
- Where:
- B is the magnetic field strength.
- A is the area of the loop.
- θ is the angle between the magnetic field and the normal to the surface of the loop.
- As the loop rotates in its own plane, the angle θ changes with time. However, since the magnetic field is uniform and constant, the magnetic field B does not change.
- The change in magnetic flux (ΔΦ) over time can be expressed as:
dΦdt=B⋅dAdt⋅cos(θ)+B⋅A⋅d(cos(θ))dt
- However, since the area A of the loop does not change and the magnetic field B is constant, the only term that could contribute to a change in flux is the term involving θ.
- According to Faraday's law of electromagnetic induction, the induced electromotive force (EMF, ε) in the loop is given by:
ε=−dΦdt
- If the magnetic flux does not change (as established earlier), then:
ε=0
- The induced current I can be calculated using Ohm's law:
I=εR
- Since the induced EMF ε=0, we have:
I=0R=0
The induced current in the loop is 0.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 251videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 114videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Problem12videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems31videos
ELECTRODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP40videos
ELECTROSTATICS
Similar Questions
A wire loop confined in a plane is rotated in its open plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
View SolutionA conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular ot one of its sides. A uniform and constant magnetic field B exists along the perpendicualr ot the plane of the loop as shown in . The current induced in the loop is
 View Solution
View SolutionA conducting square loop of side l and resistance R moves in its plane with a uniform velocity v perpendicular ot one of its sides. A uniform and constant magnetic field B exists along the perpendicualr ot the plane of the loop as shown in . The current induced in the loop is
(##HCV_VOL2_C38_E01_025_Q01##)View SolutionA semicircular loop of radius R is rotated with an angular velocity ω perpendicular to the plane of a magnetic field B as shown in the figure. Emf Induced in the loop is
 View Solution
View SolutionWhen a 'j' shaped conducting rod is rotating in its own plane with constant angular velocity ω about one of its ends P in a uniform magnetic field →B ( directed normally into the plane of paper ) the magnitude of emf induced across it will be
 View Solution
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
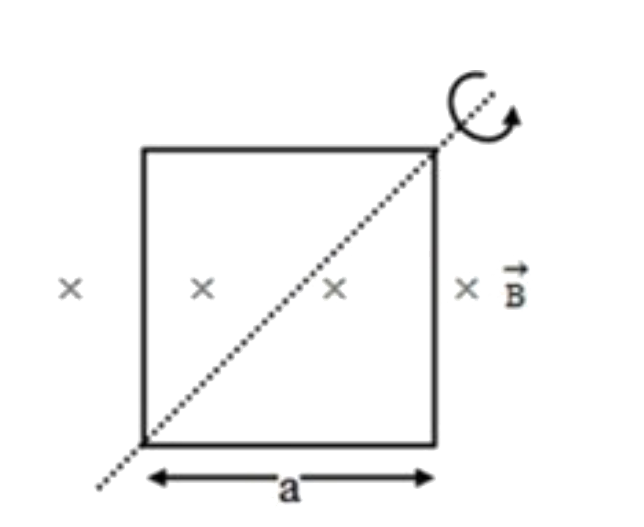 View Solution
View SolutionA circular loop of radius a having n turns is kept in a horizontal plane. A uniform magnetic field B exists in a vertical direction as shown in Fig.313. Find the emf induced in the loop if the loop is roated with a uniform angualr velocity ω about
(a) an axis passing through the center and perendicular to the plane of the loop.
(b) the diameter.
 View Solution
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.
 View Solution
View Solution

