A constant force acts on a particle and its displacement x (in cm) is related to the time t (in s) by the equation t=√x+3, when the velocity of the particle is zero, its displacement ( in cm) is
Zero
1
2
3
The correct Answer is:A
To solve the problem step by step, we will follow the reasoning provided in the video transcript.
Step 1: Understand the given equation
The relationship between displacement x (in cm) and time t (in seconds) is given by the equation:
t=√x+3
Step 2: Rearrange the equation to express x in terms of t
To find x in terms of t, we can rearrange the equation:
√x=t−3
Now, squaring both sides gives:
x=(t−3)2
Step 3: Differentiate to find velocity
Velocity v is defined as the rate of change of displacement with respect to time, which can be expressed as:
v=dxdt
Now, we differentiate x=(t−3)2:
dxdt=2(t−3)⋅d(t−3)dt
Since d(t−3)dt=1, we have:
v=2(t−3)
Step 4: Set velocity to zero to find the time
To find the time when the velocity is zero, we set v=0:
2(t−3)=0
This simplifies to:
t−3=0⟹t=3 seconds
Step 5: Find displacement at t=3
Now we substitute t=3 back into the equation for x:
x=(3−3)2=02=0 cm
Conclusion
Thus, when the velocity of the particle is zero, its displacement is:
0 cm
---
The relationship between displacement x (in cm) and time t (in seconds) is given by the equation:
t=√x+3
To find x in terms of t, we can rearrange the equation:
√x=t−3
Now, squaring both sides gives:
x=(t−3)2
Velocity v is defined as the rate of change of displacement with respect to time, which can be expressed as:
v=dxdt
Now, we differentiate x=(t−3)2:
dxdt=2(t−3)⋅d(t−3)dt
Since d(t−3)dt=1, we have:
v=2(t−3)
To find the time when the velocity is zero, we set v=0:
2(t−3)=0
This simplifies to:
t−3=0⟹t=3 seconds
Now we substitute t=3 back into the equation for x:
x=(3−3)2=02=0 cm
Thus, when the velocity of the particle is zero, its displacement is:
0 cm
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - D)
24 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
The velocity of a particle is zero at time t = 2s, then
View SolutionThe velocity of particle (whose displacement time graph is shown) at t=3
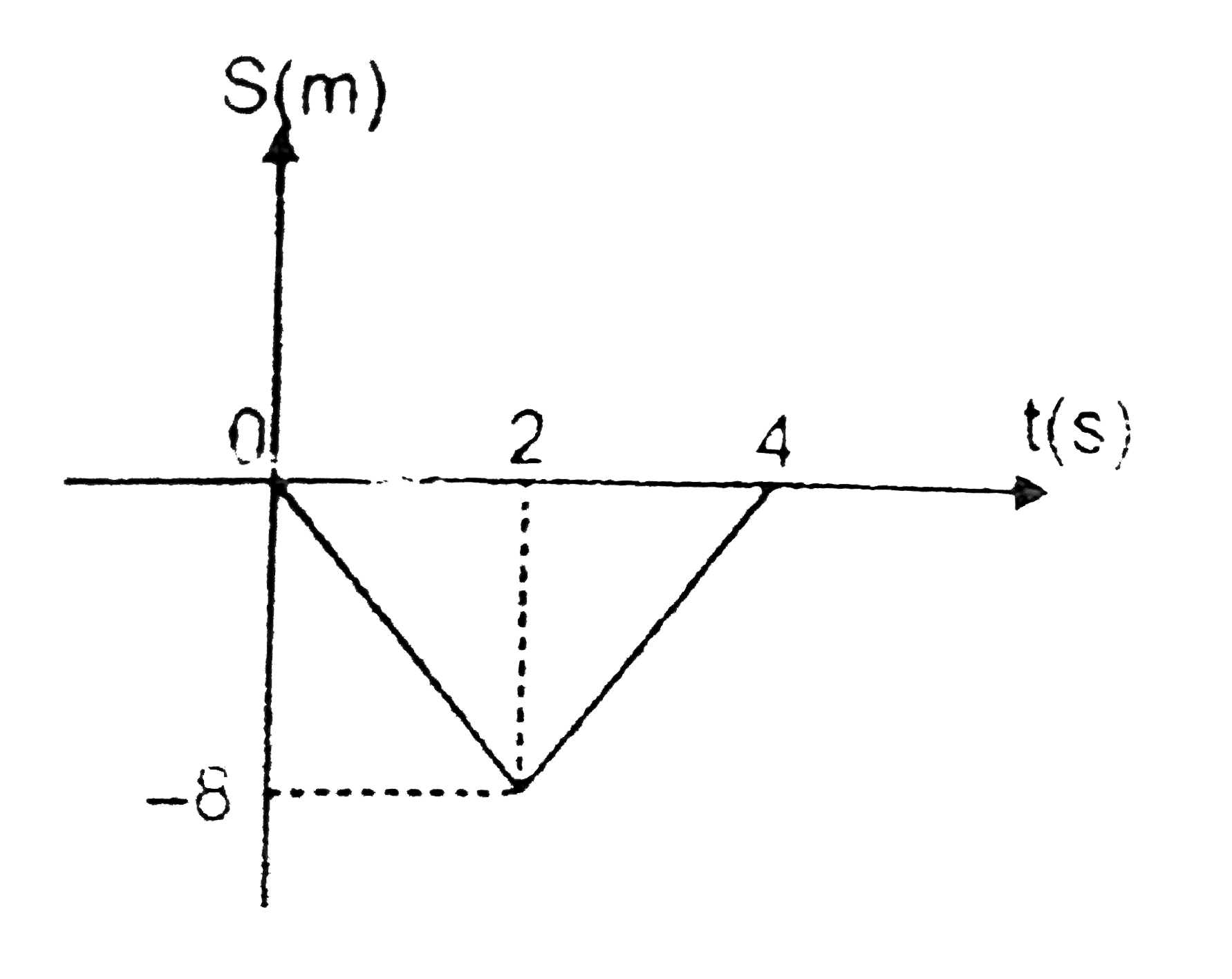 .
.
View SolutionThe displacement x of a particle moving in one dimension under the action of a constant force is related to time t by the equation t=√x+3, where x is in meter and t is in second. Find the displacement of the particle when its velocity is zero.
View SolutionThe displacement x of particle moving in one dimension, under the action of a constant force is related to the time t by the equation t=√x+3
where xis∈metersandt∈seconds . Find
(i) The displacement of the particle when its velocity is zero , and
(ii) The work done by the force in the first 6seconds.
View SolutionA particle moves along the x-axis obeying the equation x=t(t−1)(t−2), where x is in meter and t is in second
a. Find the initial velocity of the particle.
b. Find the initial acceleration of the particle.
c. Find the time when the displacement of the particle is zero.
d. Find the displacement when the velocity of the particle is zero.
e. Find the acceleration of the particle when its velocity is zero.
View SolutionThe displacement x of a particle moving in one direction is given by t=√x+3 , where x in meter and t in sec. What is its displacement when its velocity is zero
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionFor a particle moving in a straight line, the displacement of the particle at time t is given by
S=t3−6t2+3t+7
What is the velocity of the particle when its acceleration is zero?
View SolutionA particle moves along the x-direction with constant acceleration. The displacement, measured from a convenient position, is 2 m at time t=0 and is zero when t=10s. If the velocity of the particle is momentary zero when t=6s, determine the acceleration a and the velocity v when t=10s.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (s) as a=2s. The velocity of the particle is zero at zero displacement. Find the corresponding velocity-displacement equation.
View Solution
