A force F1 acts on a particle so as to accelerate it from rest to a velocity v. The force F1 is then replaced by F2 which decelerates it to rest.
F1 must be equal to F2
F1 may be equal to F2
F1 must be unequal to F2
none of these
The correct Answer is:B
To solve the problem, we will analyze the motion of the particle under the influence of the forces F1 and F2 using Newton's laws of motion.
1. Identify the Initial Conditions:
- The particle starts from rest and is accelerated to a velocity v by the force F1.
- The mass of the particle is denoted as M.
2. Acceleration During the First Phase (A to B):
- Since the particle starts from rest, the initial velocity u=0 and the final velocity v is reached.
- Let t1 be the time taken to reach velocity v.
- Using the formula for acceleration:
a=v−ut1=v−0t1=vt1
3. Applying Newton's Second Law for F1:
- According to Newton's second law, the force F1 can be expressed as:
F1=M⋅a=M⋅vt1
4. Acceleration During the Second Phase (B to C):
- In this phase, the particle is decelerated to rest, meaning the final velocity is 0 and the initial velocity is v.
- Let t2 be the time taken to come to rest.
- The acceleration during this phase can be calculated as:
a′=0−vt2=−vt2
5. Applying Newton's Second Law for F2:
- The force F2 acting on the particle can be expressed as:
F2=M⋅a′=M⋅(−vt2)=−M⋅vt2
6. Comparison of Forces F1 and F2:
- We have:
F1=M⋅vt1
F2=−M⋅vt2
- Since F1 is positive (acting in the direction of motion) and F2 is negative (acting against the direction of motion), we can conclude that:
|F1|=M⋅vt1and|F2|=M⋅vt2
7. Conclusion:
- Without knowing the relationship between t1 and t2, we cannot definitively say whether F1 is equal to F2 or not. Thus, the correct interpretation is that F1 may or may not be equal to F2.
Final Answer:
Therefore, the conclusion is that F1 may be equal to F2, but we cannot assert that they must be equal.
---
- The particle starts from rest and is accelerated to a velocity v by the force F1.
- The mass of the particle is denoted as M.
- Since the particle starts from rest, the initial velocity u=0 and the final velocity v is reached.
- Let t1 be the time taken to reach velocity v.
- Using the formula for acceleration:
a=v−ut1=v−0t1=vt1
- According to Newton's second law, the force F1 can be expressed as:
F1=M⋅a=M⋅vt1
- In this phase, the particle is decelerated to rest, meaning the final velocity is 0 and the initial velocity is v.
- Let t2 be the time taken to come to rest.
- The acceleration during this phase can be calculated as:
a′=0−vt2=−vt2
- The force F2 acting on the particle can be expressed as:
F2=M⋅a′=M⋅(−vt2)=−M⋅vt2
- We have:
F1=M⋅vt1
F2=−M⋅vt2
- Since F1 is positive (acting in the direction of motion) and F2 is negative (acting against the direction of motion), we can conclude that:
|F1|=M⋅vt1and|F2|=M⋅vt2
- Without knowing the relationship between t1 and t2, we cannot definitively say whether F1 is equal to F2 or not. Thus, the correct interpretation is that F1 may or may not be equal to F2.
Therefore, the conclusion is that F1 may be equal to F2, but we cannot assert that they must be equal.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Objective -2
9 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Exercises
42 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - worked out Examples
11 Videos
- LAWS OF THERMODYNAMICSBOOK - HC VERMA ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - All Questions
64 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
Similar Questions
A force P acts on a particle so as to accelerate it from rest to certain velocity. If P is replaced then by Q which decelerates it to rest.
View SolutionA 5kg mass is accelerated from rest to 60 m/s in 1 sec. what force acts on it:
View SolutionWhen a force F acts on a particle of mass m, the acceleration of particle becomes a. now if two forces of magnitude 3F and 4F acts on the particle simultaneously as shown in figure, then the acceleration of the particle is
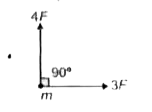
View SolutionA time dependent force F=6t acts on a particle of mass 1kg. If the particle starts from rest, the work done by the force during the first 1sec. will be
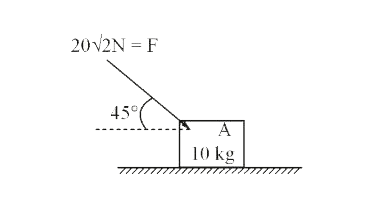
View SolutionA force F acts on a particle kept on a rough surface as shown in the figure. The particle is at rest. Find the net force applied by ground on the particle.
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
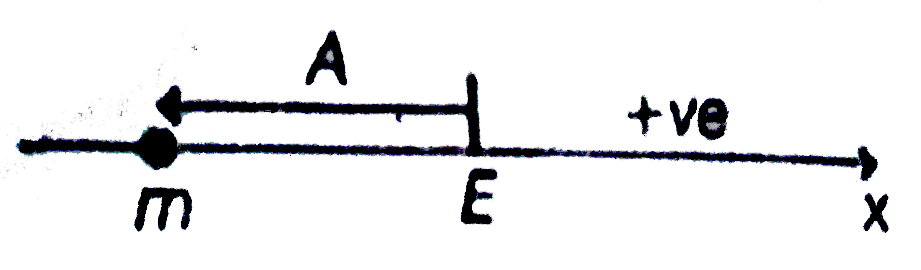
View SolutionAccording to Newton.s second law of motion, resultant force on a particle is in the direction of acceleration of the particle. Two forcce F1andF2 are acting on a particle as shown in the figure. The acceleration of the particle is along X-axis. FInd the value of F1 (in newton)
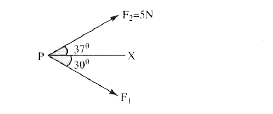
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
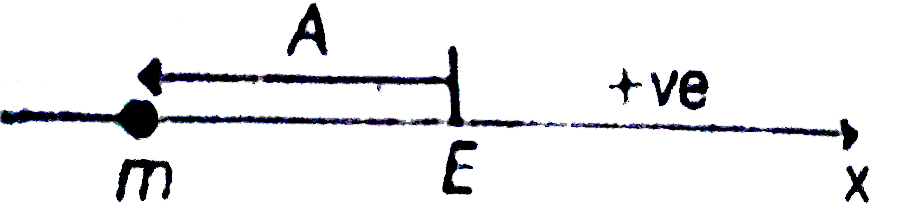
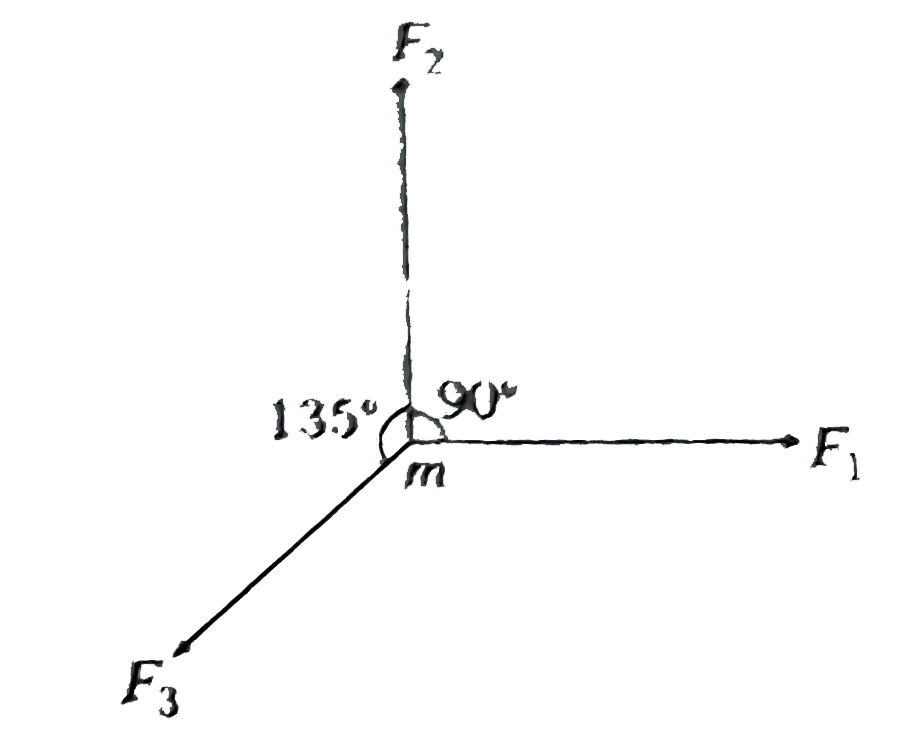
View SolutionWhen a force F acts on a body of mass m the acceleration product in the body is a . If three equal forces F1=F2=F3=F act on the same body as shown in figure the acceleration produced is
View Solution
