The nature of curve of vs. log is :
straight line
parabola
hyperbola
elliptical curve
The correct Answer is:A
To determine the nature of the curve of E∘cell vs. logKc, we can follow these steps:
1. Understand the Relationship:
We start with the Nernst equation, which relates the cell potential to the reaction quotient:
Ecell=E∘cell−0.0591nlogQ
Here, Ecell is the cell potential, E∘cell is the standard cell potential, n is the number of moles of electrons exchanged, and Q is the reaction quotient.
2. Identify Q at Equilibrium:
At equilibrium, the reaction quotient Q becomes equal to the equilibrium constant Kc. Therefore, we can rewrite the equation as:
Ecell=E∘cell−0.0591nlogKc
3. Set Ecell to Zero:
At equilibrium, Ecell becomes zero. Thus, we can set the equation to:
0=E∘cell−0.0591nlogKc
4. Rearranging the Equation:
Rearranging the equation gives us:
E∘cell=0.0591nlogKc
5. Identify the Form of the Equation:
The equation E∘cell=0.0591nlogKc can be recognized as the equation of a straight line in the form y=mx, where:
- y is E∘cell
- x is logKc
- m (the slope) is 0.0591n
6. Conclusion:
Since the relationship between E∘cell and logKc is linear, the nature of the curve of E∘cell vs. logKc is a straight line.
Final Answer:
The nature of the curve of E∘cell vs. logKc is a straight line.
We start with the Nernst equation, which relates the cell potential to the reaction quotient:
Ecell=E∘cell−0.0591nlogQ
Here, Ecell is the cell potential, E∘cell is the standard cell potential, n is the number of moles of electrons exchanged, and Q is the reaction quotient.
At equilibrium, the reaction quotient Q becomes equal to the equilibrium constant Kc. Therefore, we can rewrite the equation as:
Ecell=E∘cell−0.0591nlogKc
At equilibrium, Ecell becomes zero. Thus, we can set the equation to:
0=E∘cell−0.0591nlogKc
Rearranging the equation gives us:
E∘cell=0.0591nlogKc
The equation E∘cell=0.0591nlogKc can be recognized as the equation of a straight line in the form y=mx, where:
- y is E∘cell
- x is logKc
- m (the slope) is 0.0591n
Since the relationship between E∘cell and logKc is linear, the nature of the curve of E∘cell vs. logKc is a straight line.
The nature of the curve of E∘cell vs. logKc is a straight line.
Topper's Solved these Questions
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - LEVEL-2
28 Videos
- ELECTROCHEMISTRYBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - LEVEL-3
37 Videos
- DILUTE SOLUTIONBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - DILUTE SOLUTIONEXERCISE - leval-03
23 Videos
- GASEOUS STATEBOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Subjective problems
15 Videos
Similar Questions
Knowledge Check
Electrode potential for Mg electrode varies according to the equation
EMg2+∣Mg=EϴMg2+∣Mg−0.0592log1[Mg2+]
The graph of EMg2+∣Mgvslog[Mg2+] isA B
B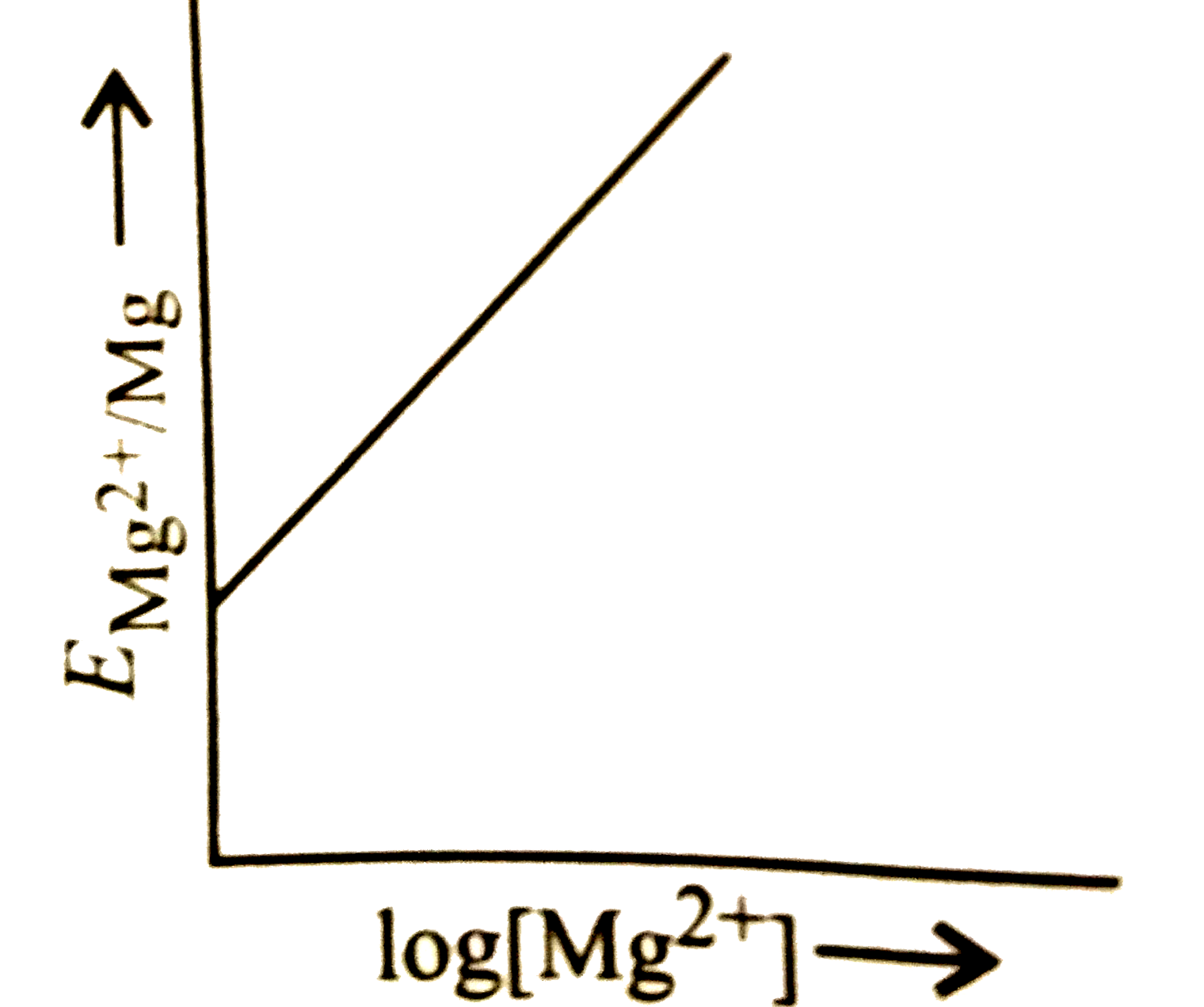 C
C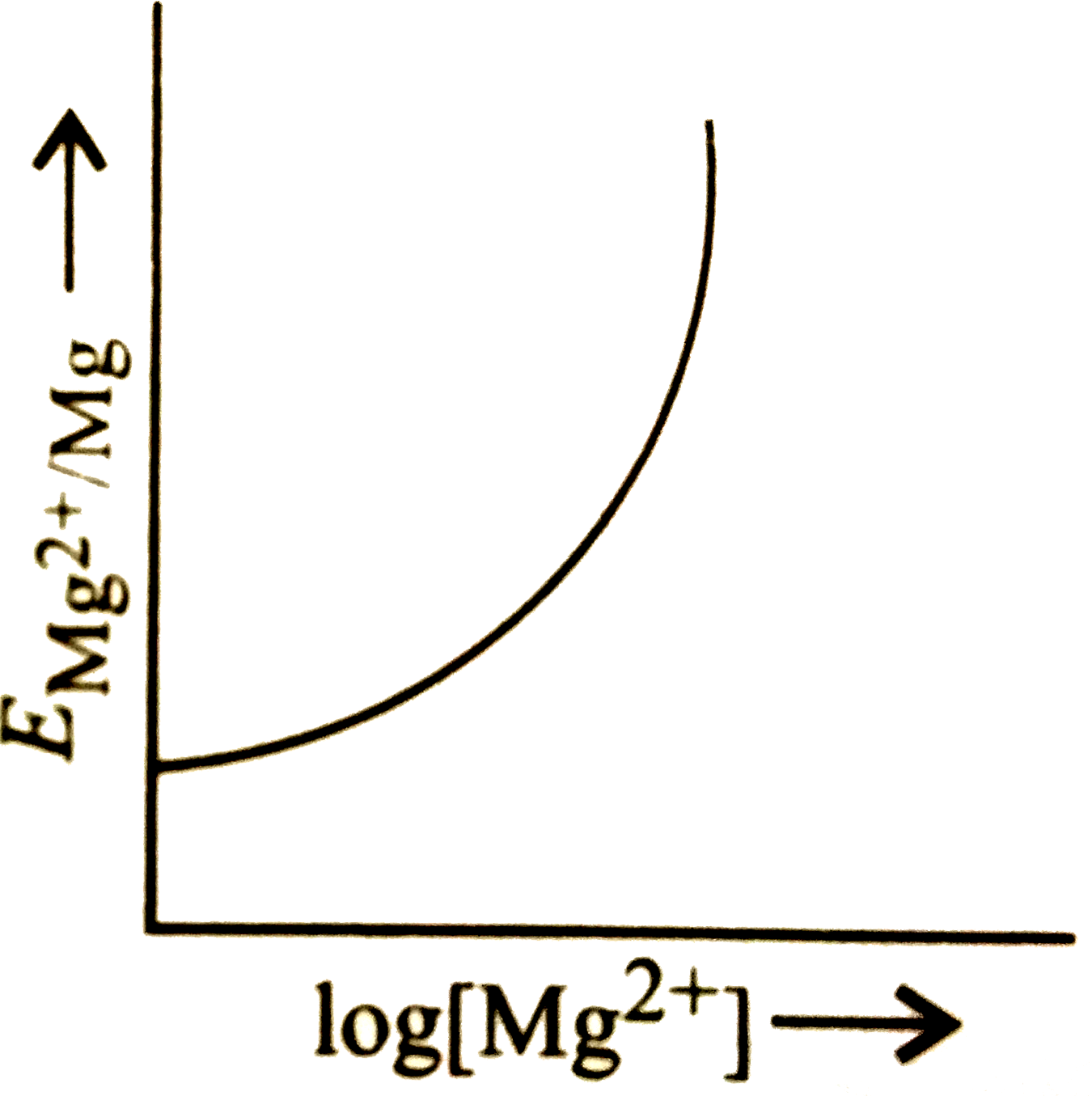 D
D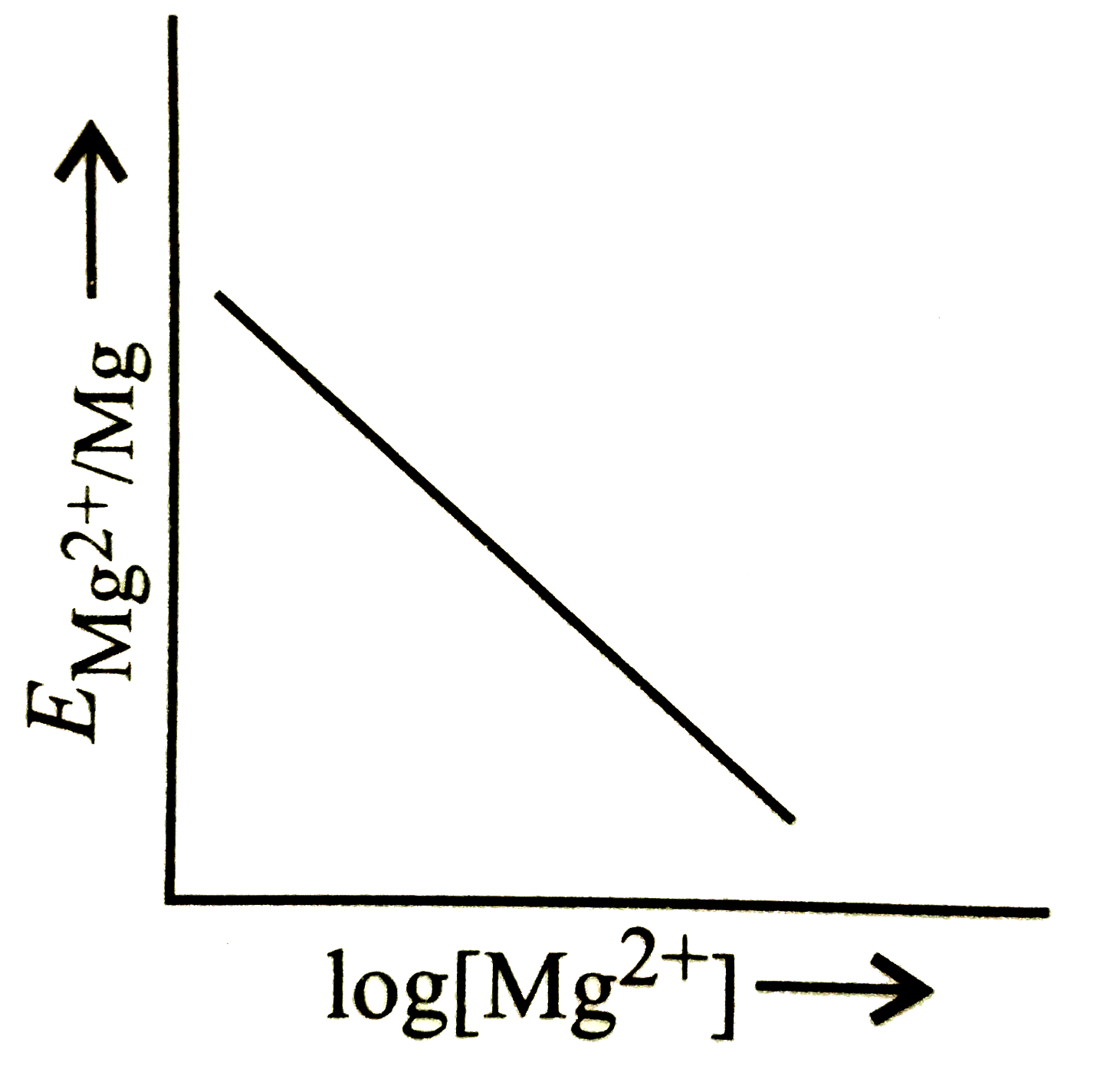
Electrode potential for Mg electrode varies according to the equation
E_(Mg^(2+)|Mg)=E_(Mg^(2+)|Mg)^(ϴ) -(0.059)/2 "log" 1/([Mg^(2+)])
The graph of EMg2+∣Mgvslog[Mg2+] is
(a)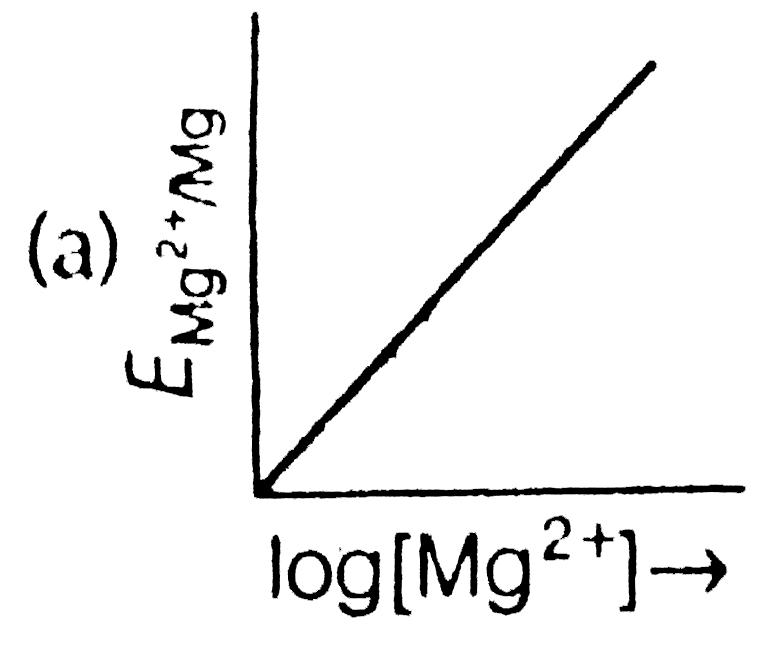
(b)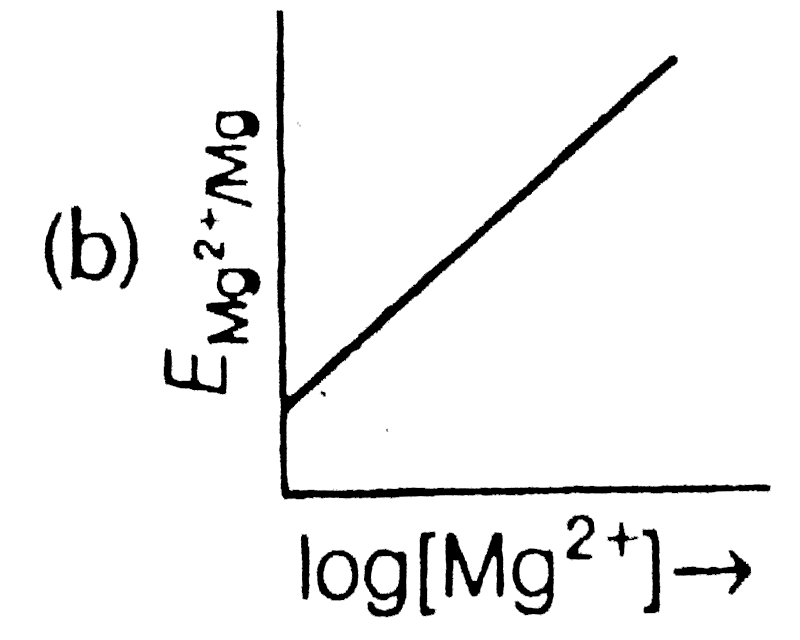
(c)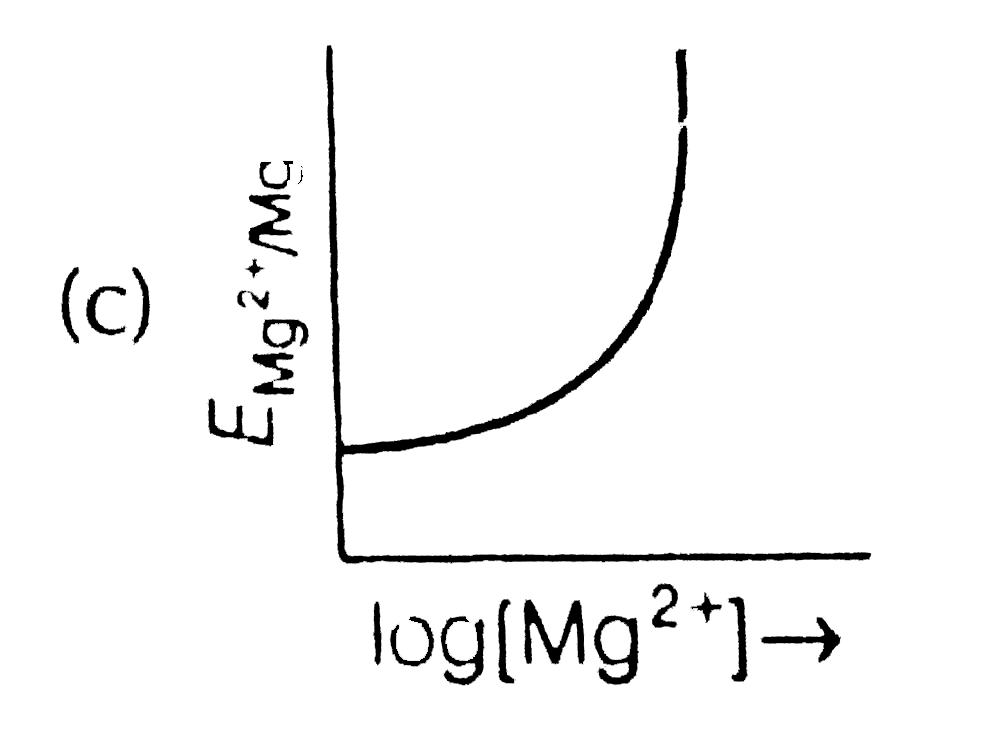
(d)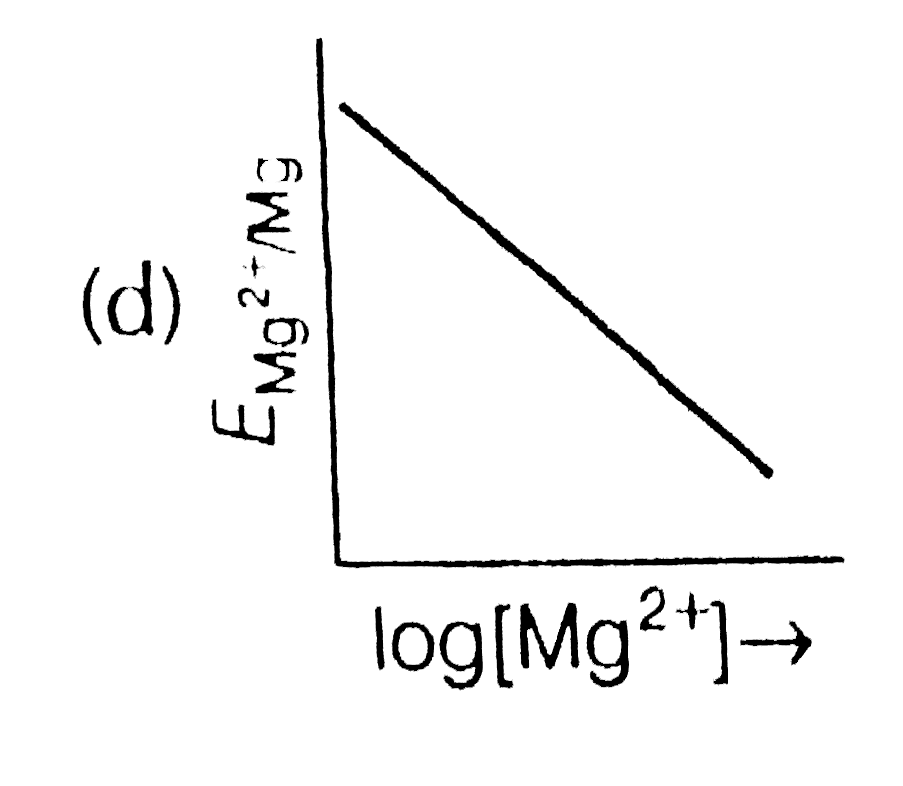
View SolutionWhy is equilibrium constant K related to only EΘcell and not Ecell?
View SolutionA graph is plotted between Ecell and log.[Zn2+][Cu2+] . The curve is linear with intercept on Ecell axis equals to 1.10V. Calculate Ecell for the cell.
Zn(s)∣∣∣∣Zn2+(0.1M)∣∣∣∣Cu2+(0.01M)∣Cu
View SolutionElectrode potential for Mg electrode varies according to the equation
EMg2+∣Mg=EϴMg2+∣Mg−0.0592log1[Mg2+]
The graph of EMg2+∣Mgvslog[Mg2+] is
View SolutionThe standard potential of Clc−|AgCl|Ag half cell is related to that of Ag⊕∣Ag though the expression.
Ec−.Ag⊕∣Ag=Ec−.Clc−|AgCl|A+RTFlnKsp(AgCl)
True/False
View SolutionThe area bounded by the curves y=logex and y=(logex)2 is (A) e−2 sq. units (B) 3−e sq. units (C) e sq. units (D) e−1 sq. units
View SolutionA graph plotted between logt12 vs log concentration is a straight line. What is your conclusion?
[Given : n = order of reaction]
View Solution
