The intercept on y-axis and slope of curve plotted between P/T vs. T
( For an ideal gas having 10 moles in a closed rigid container of volume 8.21 L. (P= Pressure in atm and T = Temp. in K, log102=0.30)) are respectively :
0.01, 0
0.1, 0
0.1, 1
10, 1
The correct Answer is:b
To solve the problem, we need to analyze the relationship between pressure (P), temperature (T), and the number of moles (n) of an ideal gas using the ideal gas law. Let's break it down step by step.
Step 1: Understand the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure (in atm)
- V = Volume (in L)
- n = Number of moles
- R = Ideal gas constant (0.0821 L·atm/(K·mol))
- T = Temperature (in K)
Step 2: Rearranging the Ideal Gas Law
We need to express P/T in terms of T:
From the ideal gas law, we can rearrange it as:
P=nRTV
Dividing both sides by T:
PT=nRV
This shows that PT is a constant (since n, R, and V are constants).
Step 3: Plotting the Graph
We are asked to plot P/T against T. This can be expressed in the form of a linear equation:
PT=nRV
This can be rewritten as:
PT=0⋅T+nRV
Where:
- The slope (m) = 0
- The y-intercept (c) = nRV
Step 4: Calculate the Intercept
Now, we need to calculate the intercept c:
Given:
- n=10 moles
- R=0.0821 L·atm/(K·mol)
- V=8.21 L
Substituting these values into the intercept formula:
c=nRV=10×0.08218.21
Calculating:
c=0.8218.21
c=0.1
Step 5: Determine the Slope
From our earlier analysis, we found that the slope m=0.
Final Answer
Thus, the intercept on the y-axis is 0.1 and the slope of the curve is 0. Therefore, the answer is:
Intercept: 0.1, Slope: 0
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = Pressure (in atm)
- V = Volume (in L)
- n = Number of moles
- R = Ideal gas constant (0.0821 L·atm/(K·mol))
- T = Temperature (in K)
We need to express P/T in terms of T:
From the ideal gas law, we can rearrange it as:
P=nRTV
Dividing both sides by T:
PT=nRV
This shows that PT is a constant (since n, R, and V are constants).
We are asked to plot P/T against T. This can be expressed in the form of a linear equation:
PT=nRV
This can be rewritten as:
PT=0⋅T+nRV
Where:
- The slope (m) = 0
- The y-intercept (c) = nRV
Now, we need to calculate the intercept c:
Given:
- n=10 moles
- R=0.0821 L·atm/(K·mol)
- V=8.21 L
c=nRV=10×0.08218.21
c=0.8218.21
c=0.1
From our earlier analysis, we found that the slope m=0.
Thus, the intercept on the y-axis is 0.1 and the slope of the curve is 0. Therefore, the answer is:
Intercept: 0.1, Slope: 0
Topper's Solved these Questions
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 230videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - GASEOUS STATEEXERCISE - Level 3 Passage 14videos
GASEOUS STATE
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - ELECTROCHEMISTRYEXERCISE - Subjective problems14videos
ELECTROCHEMISTRY
- BOOK - NARENDRA AWASTHI ENGLISHCHAPTER - IONIC EEQUILIBRIUMEXERCISE - Subjective problems1videos
IONIC EEQUILIBRIUM
Similar Questions
The intercepts and slope of graph of log K∘pVs1T are :
View SolutionA graph is plotted between p (atm) vs t∘C for 10 mol of an ideal gas as follows:
Then slope of curve and volume of container (L) respectively, are:
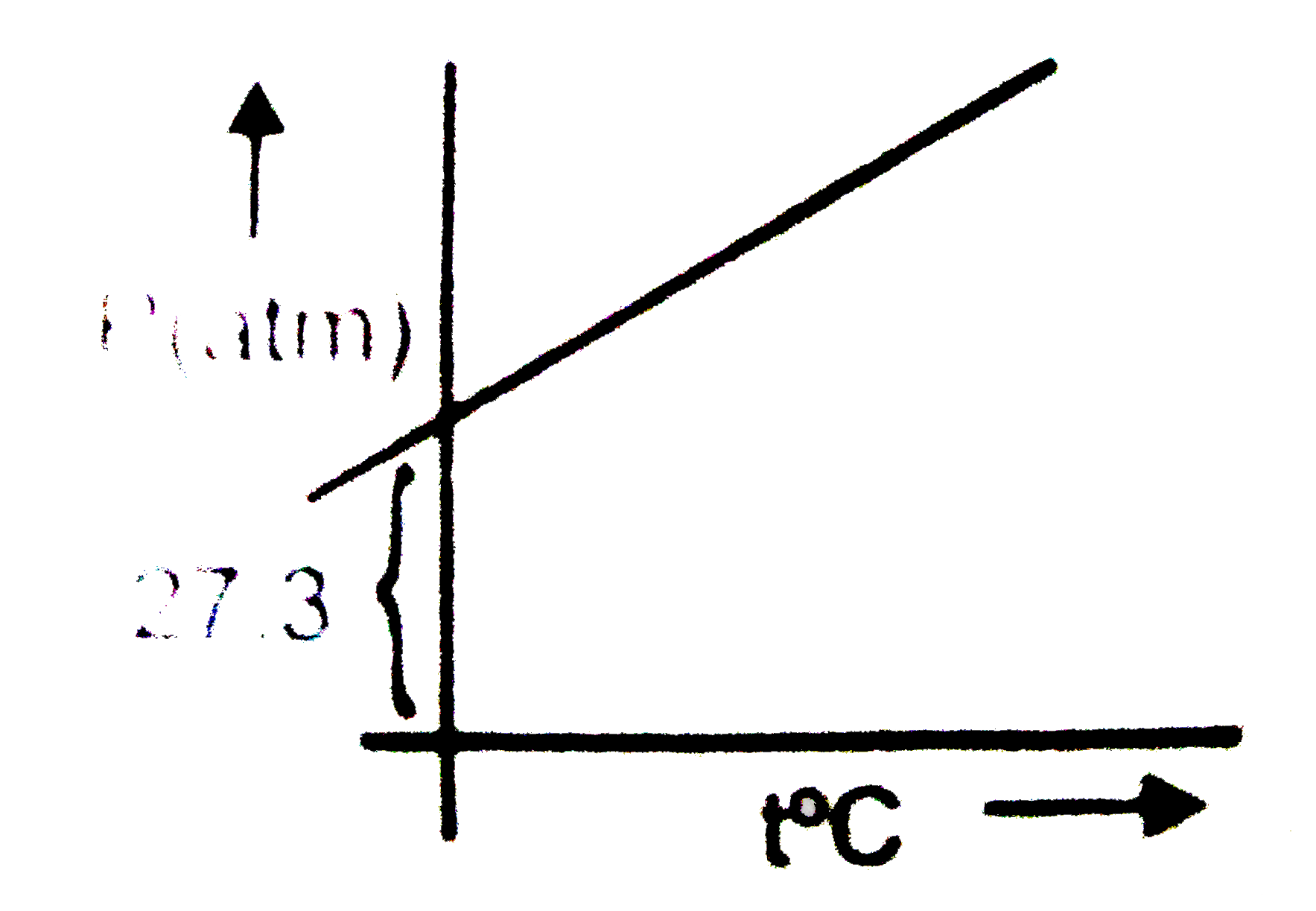 View Solution
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
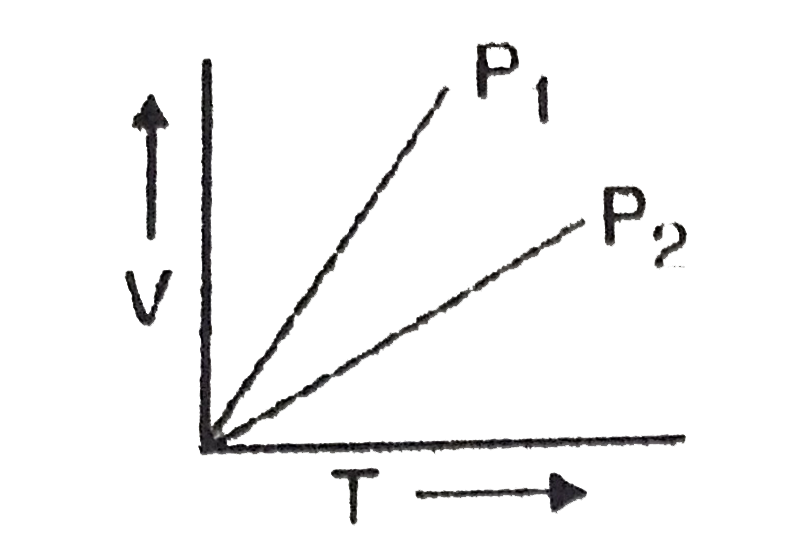
Which is correct ?View SolutionFor an ideal gas V−T curves at constant pressure P1 & P2 are shown in figure, from the figure
_E01_061_Q01.png) View Solution
View SolutionFor V versus T curves at constant pressure P1andP2 for and ideal gas shown in figure-
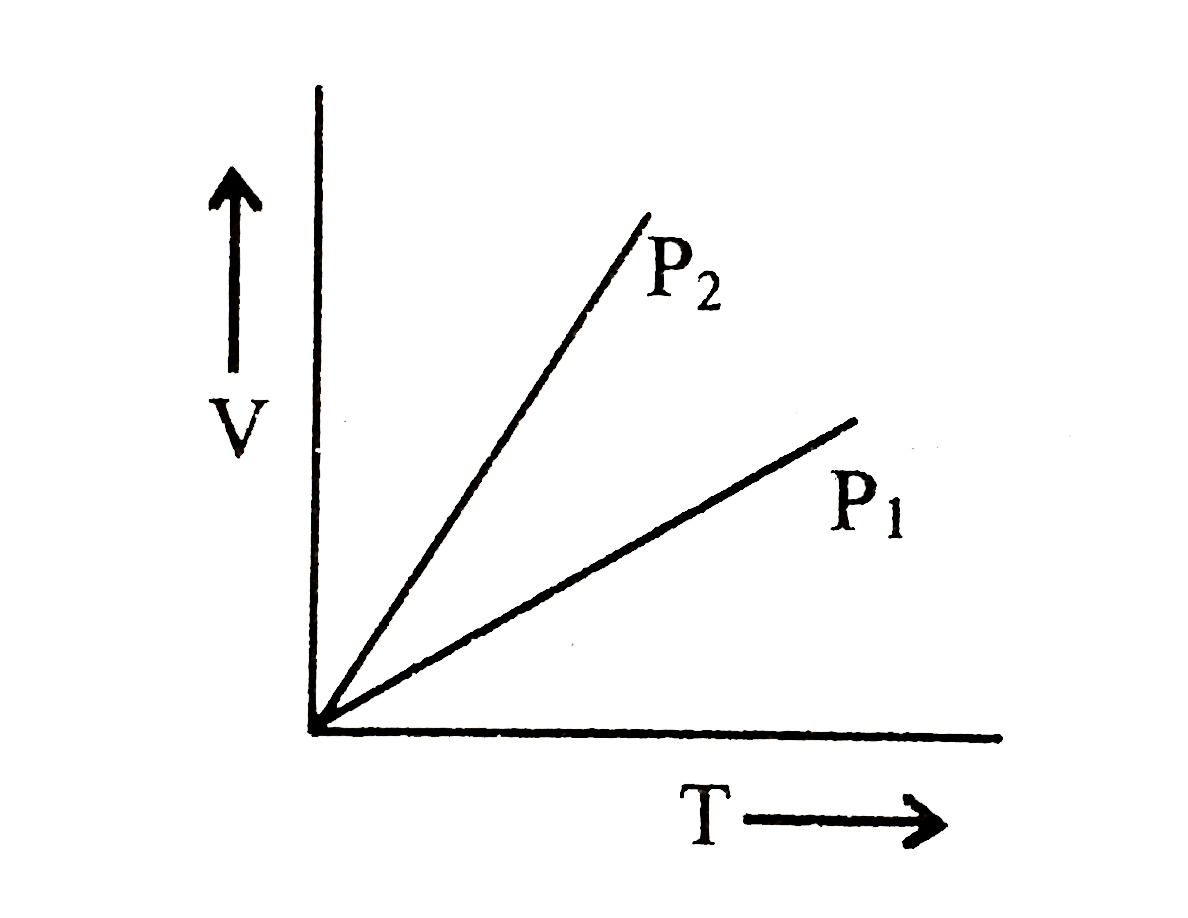 View Solution
View SolutionFor V versus T curves at constant pressure P1andP2 for an ideal gas are shown in the figure given below
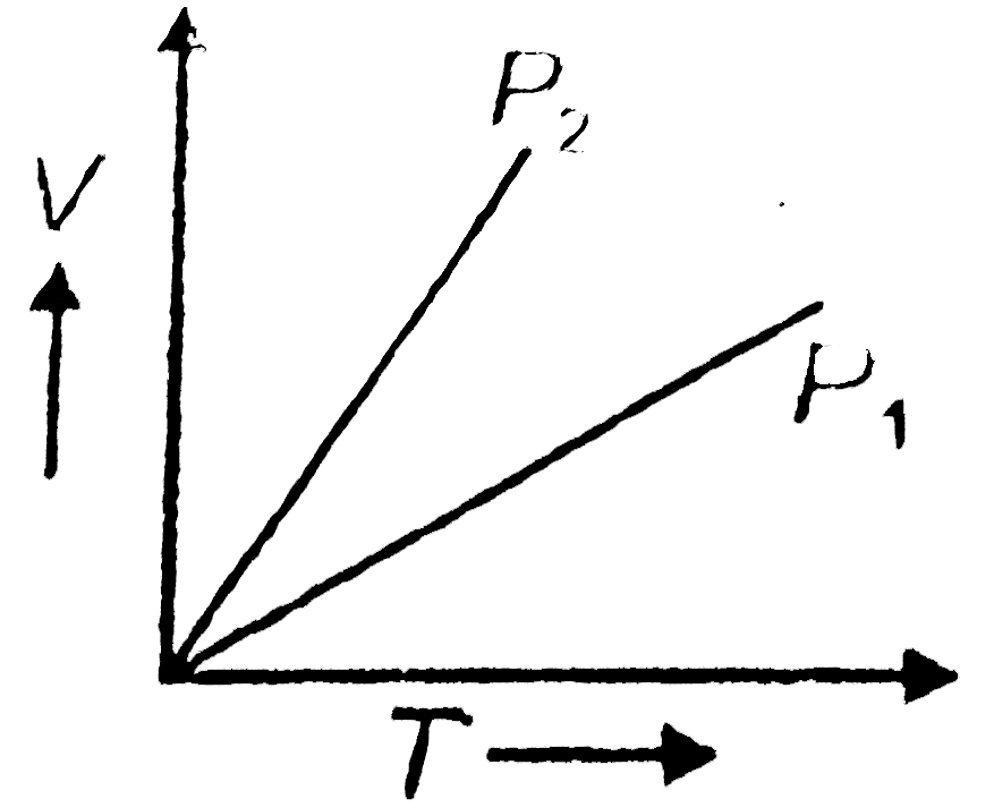 View Solution
View SolutionThe pressure of 2 mole of ideal gas at 546 K having volume 44.8 L is
View SolutionThe slope of 'P' v/s T plot at constant volume for a fixed amount of an ideal gas aus 0.01atm/K. Then what will be the value of pressure of gas (In atm) at 300K temperature ?
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown in the figure. Which of the following is correct?
 View Solution
View SolutionAt pressure P and absolute temperature T a mass M of an ideal gas fills a closed container of volume V. An additional mass 2M of the same gas is added into the container and the volume is then reduced to V3 and the temperature to T3. The pressure of the gas will now be:
View Solution

