Ratio of energy density of two steel rods is 1:4 when same mass is suspended from the rods. If length of both rods is same then ratio of diameter of rods will be.
√2:1
1:2
2:1
1:√2
The correct Answer is:√2:1
To solve the problem, we need to find the ratio of the diameters of two steel rods given that the ratio of their energy densities is 1:4 when the same mass is suspended from both rods and their lengths are the same.
1. Understanding Energy Density:
The energy density (U) in a material can be expressed as:
U=F22A2Y
where F is the force applied (which is equal to the weight of the mass suspended), A is the cross-sectional area of the rod, and Y is Young's modulus of the material.
2. Given Information:
- The energy density ratio of the two rods is given as U1U2=14.
- The lengths of both rods are the same, and the same mass is suspended from both.
3. Relating Energy Density to Area:
Since the force F and Young's modulus Y are the same for both rods, we can simplify the ratio of energy densities:
U1U2=A22A21
Therefore, we can write:
A21A22=14
4. Expressing Area in Terms of Diameter:
The cross-sectional area A of a rod can be expressed in terms of its diameter d:
A=πd24
Thus, we can write:
A1=πd214andA2=πd224
5. Substituting Areas into the Ratio:
Now substituting the expressions for A1 and A2 into the ratio:
A21A22=(πd214)2(πd224)2=d41d42
Therefore, we have:
d41d42=14
6. Taking the Square Root:
Taking the square root of both sides gives:
d21d22=12
7. Finding the Diameter Ratio:
Taking the square root again, we find:
d1d2=1√2
Hence, the ratio of diameters d1:d2 is:
d1:d2=√2:1
Final Answer:
The ratio of the diameters of the two rods is √2:1.
The energy density (U) in a material can be expressed as:
U=F22A2Y
where F is the force applied (which is equal to the weight of the mass suspended), A is the cross-sectional area of the rod, and Y is Young's modulus of the material.
- The energy density ratio of the two rods is given as U1U2=14.
- The lengths of both rods are the same, and the same mass is suspended from both.
Since the force F and Young's modulus Y are the same for both rods, we can simplify the ratio of energy densities:
U1U2=A22A21
Therefore, we can write:
A21A22=14
The cross-sectional area A of a rod can be expressed in terms of its diameter d:
A=πd24
Thus, we can write:
A1=πd214andA2=πd224
Now substituting the expressions for A1 and A2 into the ratio:
A21A22=(πd214)2(πd224)2=d41d42
Therefore, we have:
d41d42=14
Taking the square root of both sides gives:
d21d22=12
Taking the square root again, we find:
d1d2=1√2
Hence, the ratio of diameters d1:d2 is:
d1:d2=√2:1
The ratio of the diameters of the two rods is √2:1.
Topper's Solved these Questions
Similar Questions
A uniform thin rod of length l is suspended from one of its ends and is rotated at f rotations per second. The rotational kinetic energy of the rod will be
View SolutionThe ratio of the thermal conductivities of two different materials is 1:2. The thermal resistance of the rods of these materials having the same thickness are equal. Find the ratio of the length of rods.
View Solution
Knowledge Check
- Question 1 - Select One
Heat is flowing through two cylindrical rods of the same material. The diamters of the rods are in the ratio 1:2 and the length in the ratio 2:1. If the temperature difference between the ends is same then ratio of the rate of flow of heat through them will be
A1:1B1:8C2:1D8:1
A uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View SolutionA uniform steel rod of cross- sectional area A and L is suspended so that it hangs vertically. The stress at the middle point of the rod is
View SolutionA thin rod of negligible mass and area of cross section S is suspended vertically from one end. Length of the rod is L0 at T∘C . A mass m is attached to the lower end of the rod so that when temperature of the rod is reduced to 0∘C its length remains L0 Y is the Young’s modulus of the rod and α is coefficient of linear expansion of rod. Value of m is :
View SolutionThe ratio of the diameters of two metallic rods of the same material is 2:1 and their lengths are in the ratio 1:4. If the temperature difference between their ends are equal, the rate of flow of heat in them will be in the ratio
View SolutionFour rods of same material and having the same cross section and length have been joined, as shown. The temperature of the junction of four rods will be :
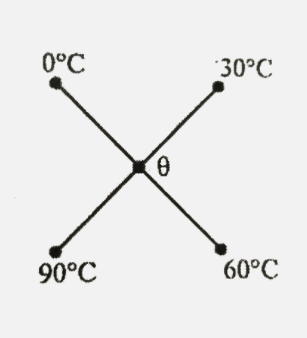 View Solution
View SolutionMoment of inertia of a rigid body is expressed in units of kg m2. There are two rods A and B made of same metal. Both of them have equal cross-sectional area bur rod A is double in length as compared to rod B. What is the ratio of moment of ineria of rod A to that of rod B?
View SolutionIn the arrangement shown in figure the mass of the ball is η times as that of the rod. The length of the rod is L the masses of the pulleys and the threads as well as the friction, are negligible. The ball is set on the same level as the lower end of the rod and then released. How soon will the ball be opposite the upper end of the rod?
 View Solution
View Solution

