A uniform wire of resistance 9Ω is joined end-to-end to from a circle. Then, the resistance of the circular wire between any two diametrically points is
6Ω
3Ω
94Ω
32Ω
The correct Answer is:C
To find the resistance of a circular wire formed by joining a uniform wire of resistance 9Ω end-to-end between any two diametrically opposite points, we can follow these steps:
1. Understanding the Problem:
We have a circular wire made from a uniform wire with a total resistance of 9Ω. We need to find the resistance between two points that are diametrically opposite on the circle.
2. Dividing the Circle:
When we consider two diametrically opposite points on the circle, the circular wire can be thought of as being divided into two equal halves. Each half will have a resistance of:
Rhalf=Rtotal2=9Ω2=4.5Ω
3. Setting Up the Circuit:
The two halves of the wire can be treated as two resistors in parallel. Let’s denote the resistance of each half as R1 and R2:
R1=R2=4.5Ω
4. Calculating Equivalent Resistance:
The formula for the equivalent resistance R′ of two resistors in parallel is given by:
1R′=1R1+1R2
Substituting the values:
1R′=14.5+14.5=24.5=292=49
Therefore,
R′=94Ω
5. Conclusion:
The resistance of the circular wire between any two diametrically opposite points is:
R′=94Ω
Final Answer:
The resistance between any two diametrically opposite points is 94Ω.
We have a circular wire made from a uniform wire with a total resistance of 9Ω. We need to find the resistance between two points that are diametrically opposite on the circle.
When we consider two diametrically opposite points on the circle, the circular wire can be thought of as being divided into two equal halves. Each half will have a resistance of:
Rhalf=Rtotal2=9Ω2=4.5Ω
The two halves of the wire can be treated as two resistors in parallel. Let’s denote the resistance of each half as R1 and R2:
R1=R2=4.5Ω
The formula for the equivalent resistance R′ of two resistors in parallel is given by:
1R′=1R1+1R2
Substituting the values:
1R′=14.5+14.5=24.5=292=49
Therefore,
R′=94Ω
The resistance of the circular wire between any two diametrically opposite points is:
R′=94Ω
The resistance between any two diametrically opposite points is 94Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Knowledge Check
A uniform wire of resistance 36Ω is bent in the form of a circle. The effective resistance across the points A and B is
 A5ΩB15ΩC7.2ΩD30Ω
A5ΩB15ΩC7.2ΩD30ΩA wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is
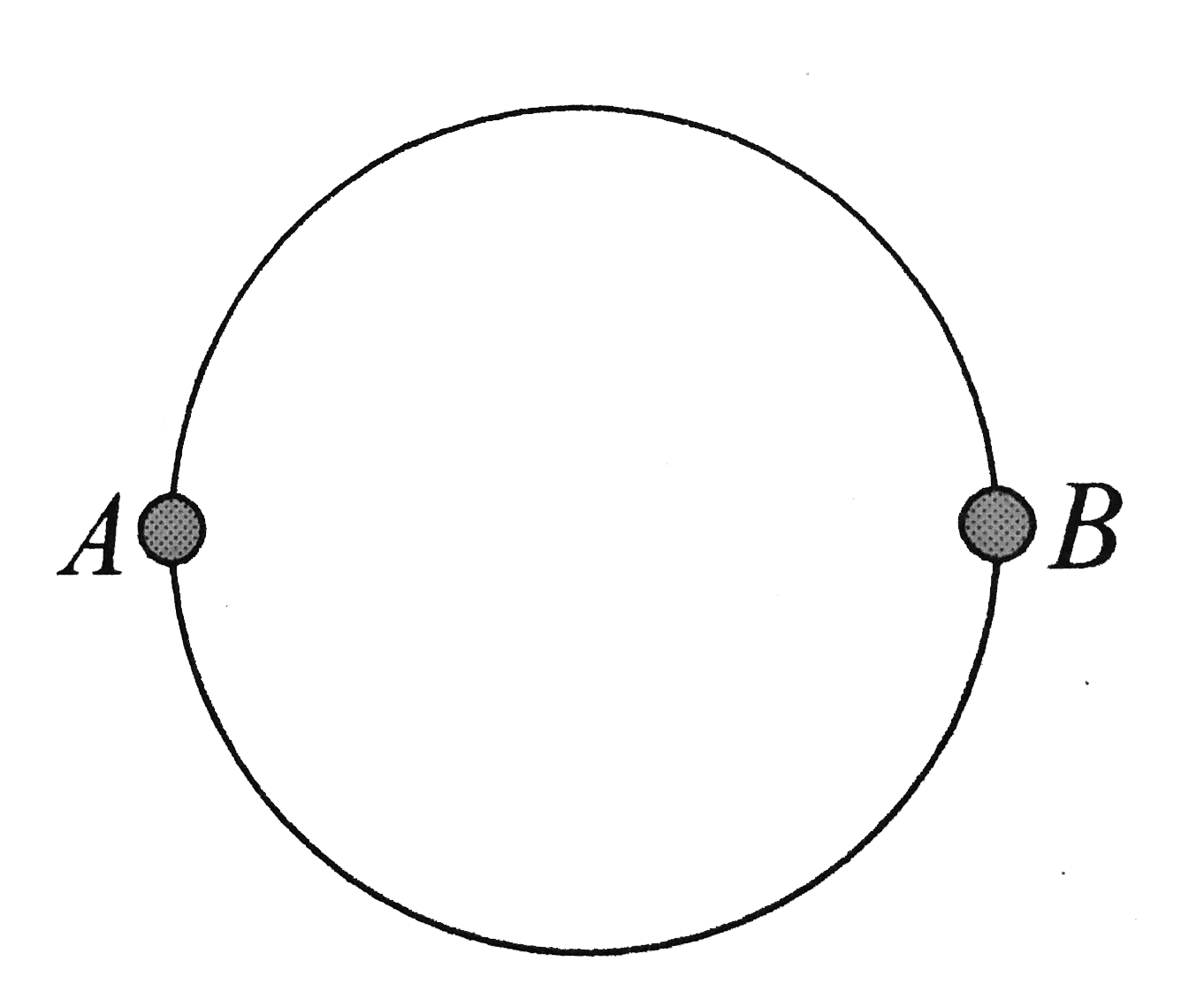 A3ΩB6πΩC6ΩD0.6πΩ
A3ΩB6πΩC6ΩD0.6πΩ
A uniform wire os resistance 12Ω is bent to form a circle. Effective resistance across two diametrically opposite points is
View SolutionA metallic wire having a resistance of 20Ω is bent in order to form a complete circle. Calculate the resistance between any two diametrically opposite points on the circle.
View SolutionA wire of resistance 20Ω is bent to form a complete circle. The resistance between two diametrically opposite points A and B as shown in the figure, is
View SolutionA wire of resistance 4Ω is stretched to twice its original length. The resistance of stretched wire would be
View SolutionA uniform wire of resistance 36Ω is bent in the form of a circle. The Effective resistance between A and B is (O is the centre of circle):

View SolutionA wire of resistance 12Ωm−1 is bent to from a complete circle of radius 10cm. The resistance between its two diametrically opposite points, A and B as shown in the figure, is

View Solution

_PHY_E05_303_Q01.png)