The moment of inertia of a solid sphere, about an axis parallel to its diameter and at a distance of x form it is, 'I(x)'. Which one of the graphs represents the variation of 'I(x) with x correctly ?
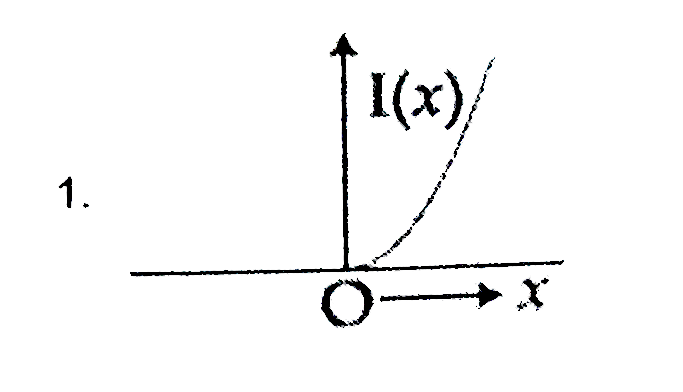



The correct Answer is:A
To solve the problem of finding the moment of inertia I(x) of a solid sphere about an axis parallel to its diameter and at a distance x from it, we can follow these steps:
1. Understand the Moment of Inertia:
The moment of inertia I about an axis is a measure of how difficult it is to change the rotational motion of an object about that axis. For a solid sphere, the moment of inertia about an axis through its center (CM) is given by:
ICM=25mR2
where m is the mass of the sphere and R is its radius.
2. Use the Parallel Axis Theorem:
To find the moment of inertia about an axis that is parallel to the diameter and at a distance x from it, we can use the Parallel Axis Theorem:
I(x)=ICM+md2
where d is the distance from the center of mass axis to the new axis. In this case, d=x.
3. Substitute the Values:
Substitute ICM and d into the equation:
I(x)=25mR2+mx2
4. Rearranging the Equation:
The equation can be rearranged as:
I(x)=mx2+25mR2
This shows that I(x) is a quadratic function of x.
5. Identify the Characteristics of the Graph:
The equation I(x)=mx2+25mR2 is a parabola that opens upwards. The y-intercept (when x=0) is 25mR2, which is a positive value. This means the graph will not pass through the origin.
6. Conclusion:
The correct graph representing the variation of I(x) with x will be a parabola that starts from the point (0,25mR2) and opens upwards.
The moment of inertia I about an axis is a measure of how difficult it is to change the rotational motion of an object about that axis. For a solid sphere, the moment of inertia about an axis through its center (CM) is given by:
ICM=25mR2
where m is the mass of the sphere and R is its radius.
To find the moment of inertia about an axis that is parallel to the diameter and at a distance x from it, we can use the Parallel Axis Theorem:
I(x)=ICM+md2
where d is the distance from the center of mass axis to the new axis. In this case, d=x.
Substitute ICM and d into the equation:
I(x)=25mR2+mx2
The equation can be rearranged as:
I(x)=mx2+25mR2
This shows that I(x) is a quadratic function of x.
The equation I(x)=mx2+25mR2 is a parabola that opens upwards. The y-intercept (when x=0) is 25mR2, which is a positive value. This means the graph will not pass through the origin.
The correct graph representing the variation of I(x) with x will be a parabola that starts from the point (0,25mR2) and opens upwards.
Similar Questions
Moment of inertia I of a solid sphere about an axis parallel to a diameter and at a distance x from it varies as:
View SolutionFigure represents the moment of inertia of the solid sphere about an axis parallel to the diameter of the solid sphere and at a distance x from t. Which one of the following represents the variations of I with x ?
View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View SolutionWhat is the moment of inertia of a circular disc about one of its diameters ?
View SolutionThe moment of inertia of a solid sphere of radius R about its diameter is same as that of a disc of radius 2R about its diameter. The ratio of their masses is
View SolutionA square plate has a moment of inertia l0 about an axis lying in its plane, passing through its centre and making an angle θ with one of the sides. Which graph represents the variation of l with θ ?
View SolutionMoment of inertia of a disc about an axis parallel to diameter and at a distance x from the centre of the disc is same as the moment of inertia of the disc about its centre axis. The radius of disc is R. The value of x is
View SolutionThe moment of inertia of cylinder of radius a, mass M and height h about an axis parallel to the axis of the cylinder and distance b from its centre is :
View SolutionWhich of the following graphs best represents the variation of acceleration 'a' with displacement x?
View Solution

