A square plate has a moment of inertia l0 about an axis lying in its plane, passing through its centre and making an angle θ with one of the sides. Which graph represents the variation of l with θ ?
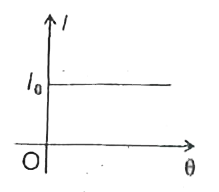

The correct Answer is:C
To solve the problem of how the moment of inertia I of a square plate varies with the angle θ of the axis passing through its center, we can follow these steps:
1. Understanding the Moment of Inertia:
The moment of inertia I of an object about a given axis is a measure of how difficult it is to change its rotational motion about that axis. For a square plate, the moment of inertia depends on the distribution of mass relative to the axis of rotation.
2. Defining the Square Plate:
Consider a square plate with uniform mass distribution. Let the side length of the square be a. The mass of the plate can be denoted as m.
3. Identifying the Axis of Rotation:
The axis of rotation is in the plane of the square and passes through its center, making an angle θ with one of the sides of the square.
4. Using the Parallel Axis Theorem:
The moment of inertia about an axis through the center of mass (CM) can be calculated using the formula:
ICM=16ma2
This is the moment of inertia about an axis perpendicular to the plane of the square.
5. Considering the Angle θ:
When the axis is tilted at an angle θ, the distribution of mass relative to the new axis changes. However, due to the symmetry of the square, the moment of inertia remains constant regardless of the angle θ.
6. Conclusion:
Since the axis divides the square symmetrically and the mass distribution remains uniform, the moment of inertia I does not depend on the angle θ. Thus, we can conclude that:
I(θ)=I0(constant)
7. Graph Representation:
The graph representing the variation of I with θ will be a horizontal line, indicating that I remains constant as θ varies. Therefore, the correct graph is option C.
The moment of inertia I of an object about a given axis is a measure of how difficult it is to change its rotational motion about that axis. For a square plate, the moment of inertia depends on the distribution of mass relative to the axis of rotation.
Consider a square plate with uniform mass distribution. Let the side length of the square be a. The mass of the plate can be denoted as m.
The axis of rotation is in the plane of the square and passes through its center, making an angle θ with one of the sides of the square.
The moment of inertia about an axis through the center of mass (CM) can be calculated using the formula:
ICM=16ma2
This is the moment of inertia about an axis perpendicular to the plane of the square.
When the axis is tilted at an angle θ, the distribution of mass relative to the new axis changes. However, due to the symmetry of the square, the moment of inertia remains constant regardless of the angle θ.
Since the axis divides the square symmetrically and the mass distribution remains uniform, the moment of inertia I does not depend on the angle θ. Thus, we can conclude that:
I(θ)=I0(constant)
The graph representing the variation of I with θ will be a horizontal line, indicating that I remains constant as θ varies. Therefore, the correct graph is option C.
Similar Questions
The moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle θ with the line joining its ends ( as shown ) is
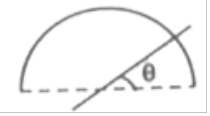
View SolutionThe moment of inertia of a solid sphere, about an axis parallel to its diameter and at a distance of x form it is, 'I(x)'. Which one of the graphs represents the variation of 'I(x) with x correctly ?
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is

View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionFigure shows the variation of the moment of inertia of a uniform rod, about an axis passing through itss centre and inclined at an angle θ to the length. The moment of inertia of the rod about an axis passing through one of its ends and making an angle θ=π3 will be
View Solution
A square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one one of its corner is
View SolutionA square is made by joining four rods each of mass M and length L. Its moment of inertia about an axis PQ, in its plane and passing through one of its corner is

View Solution