A particle of mass m is acted upon by a force F given by the emprical law F=Rt2υ(t)
If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot :
υ(t)against t2
log υ(t) anainst 1t2
log υ(t) against t
logυ(t) against 1t
To solve the problem step by step, we will analyze the given force equation and apply Newton's second law to derive the relationship between velocity and time.
Step 1: Write down the force equation
Given the empirical law:
F=Rt2v(t)
Step 2: Apply Newton's second law
According to Newton's second law, the force can also be expressed as:
F=mdvdt
where m is the mass of the particle and dvdt is the acceleration.
Step 3: Set the two expressions for force equal to each other
Equating the two expressions for force, we have:
mdvdt=Rt2v(t)
Step 4: Rearrange the equation
Rearranging gives us:
dvv(t)=Rm1t2dt
Step 5: Integrate both sides
Now we will integrate both sides. The left side integrates with respect to v and the right side with respect to t:
∫dvv(t)=∫Rm1t2dt
The left side gives:
ln|v(t)|
The right side integrates to:
−Rm1t+C
where C is the constant of integration.
Step 6: Combine the results
Thus, we have:
ln|v(t)|=−Rm1t+C
Step 7: Exponentiate both sides
Exponentiating both sides gives:
v(t)=eCe−Rm1t
Let K=eC, then:
v(t)=Ke−Rm1t
Step 8: Analyze the relationship
From the equation v(t)=Ke−Rm1t, we see that lnv(t) is a linear function of 1t:
lnv(t)=lnK−Rm1t
Step 9: Conclusion
This indicates that if we plot lnv(t) against 1t, we should obtain a straight line.
Final Answer
The best way to test the empirical law experimentally is to plot:
lnv(t) against 1t
---
Given the empirical law:
F=Rt2v(t)
According to Newton's second law, the force can also be expressed as:
F=mdvdt
where m is the mass of the particle and dvdt is the acceleration.
Equating the two expressions for force, we have:
mdvdt=Rt2v(t)
Rearranging gives us:
dvv(t)=Rm1t2dt
Now we will integrate both sides. The left side integrates with respect to v and the right side with respect to t:
∫dvv(t)=∫Rm1t2dt
ln|v(t)|
−Rm1t+C
where C is the constant of integration.
Thus, we have:
ln|v(t)|=−Rm1t+C
Exponentiating both sides gives:
v(t)=eCe−Rm1t
v(t)=Ke−Rm1t
From the equation v(t)=Ke−Rm1t, we see that lnv(t) is a linear function of 1t:
lnv(t)=lnK−Rm1t
This indicates that if we plot lnv(t) against 1t, we should obtain a straight line.
The best way to test the empirical law experimentally is to plot:
lnv(t) against 1t
Topper's Solved these Questions
Similar Questions
A particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionThe velocity →v of a particle of mass 'm' acted upon by a constant force is given by →v(t)=A[cos(kt)¯i−sin(kt)¯j] . Then the angle between the force and the momentum of the particle is (Here A and k are constants)
View SolutionA particle is acted upon by a force given by F=(12t−3t2)N, where is in seconds. Find the change in momenum of that particle from t=1 to t=3 sec.
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
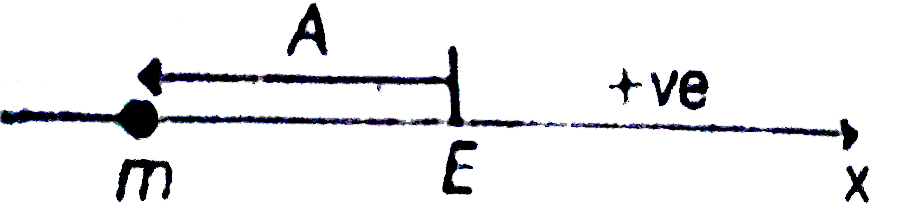
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
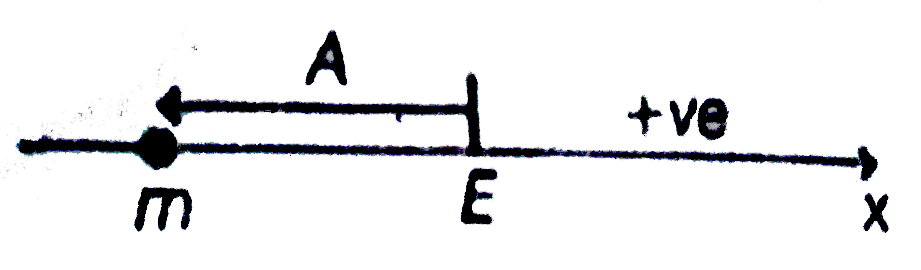
View SolutionA particle of mass m initially at rest is acted upon by a unidirectional force F=F∘cos(π2t). The distance travelled by the particle when it stops first in the subsequent motion is ,
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA particle of mass m is driven by a machine that delivers a constant power k watts. If the particle starts from rest the force on the particle at time t is
View SolutionA particle of mass 70 g, moving at 50 cm/s , is acted upon by a variable force opposite to its direction of motion. The force F is shown as a function of time t
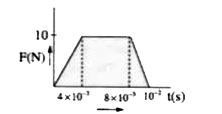
(a) its speed will be 50 cm/s after the force stops acting
(b) its direction of motion will reverse
(c) its average acceleration will be 1m/s2 during the interval in which the force acts
its average acceleration will be 10m/s2 during the interval in which the force acts
View Solution
