A particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
its displacement will be in simple harmonic
its velocity will be in simple harmonic
its acceleration will be in simple harmonic
None of the above
The correct Answer is:D
To solve the problem, we need to analyze the force acting on the particle and determine whether its motion can be classified as simple harmonic motion (SHM).
1. Understanding the Force:
The force acting on the particle is given by:
F=t2−kx
where t is time, k is a constant, and x is the displacement of the particle.
2. Condition for Simple Harmonic Motion:
For a particle to exhibit simple harmonic motion, the restoring force must be proportional to the negative of the displacement:
F=−kx
This means that the force should only depend on the displacement x and not on time t.
3. Analyzing the Given Force:
In the given force F=t2−kx, we can see that there is a term t2 which depends on time. This indicates that the force is not solely dependent on the displacement x.
4. Conclusion on Motion Type:
Since the force has a time-dependent term t2, it cannot satisfy the condition for SHM. Therefore, the particle will not undergo simple harmonic motion.
5. Evaluating the Statements:
- Statement A: The displacement will be in SHM. (False)
- Statement B: The velocity will be in SHM. (False)
- Statement C: The acceleration will be in SHM. (False)
- Statement D: None of the above. (True)
Thus, the correct answer is that none of the statements are correct.
Final Answer:
D: None of the above.
The force acting on the particle is given by:
F=t2−kx
where t is time, k is a constant, and x is the displacement of the particle.
For a particle to exhibit simple harmonic motion, the restoring force must be proportional to the negative of the displacement:
F=−kx
This means that the force should only depend on the displacement x and not on time t.
In the given force F=t2−kx, we can see that there is a term t2 which depends on time. This indicates that the force is not solely dependent on the displacement x.
Since the force has a time-dependent term t2, it cannot satisfy the condition for SHM. Therefore, the particle will not undergo simple harmonic motion.
- Statement A: The displacement will be in SHM. (False)
- Statement B: The velocity will be in SHM. (False)
- Statement C: The acceleration will be in SHM. (False)
- Statement D: None of the above. (True)
D: None of the above.
Similar Questions
A particle of mass m is acted upon by a force F given by the emprical law F=Rt2υ(t)
If this law is to be tested experimentally by observing the motion starting from rest, the best way is to plot :
View SolutionA particle of mass m is acted on by two forces of equal magnitude F maintaining their orientation relative to the velocity v as shown in Fig. The momentum of the particle

View Solution
Knowledge Check
A particle is acted upon by a force F which varies with position x is shown in figure .If the particle at x=0 kinetic energy of 25J then the kinetic energy of the particle at x=16m is
 A45 JB30 JC70 JD20 J
A45 JB30 JC70 JD20 J
Passage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
What it is the time period of periodic motion of particle.
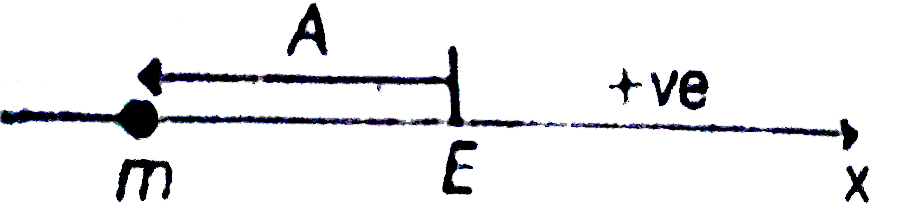
View SolutionPassage XII)_ A particle of mass m is constrained to move along x-axis. A force F acts on the particle. F always points toward the position labelled E. For example, when the particle is to the left of E,Fpoints to the right. The magnitude of F is consant except at point E where it is zero. The systm is horizontal. F is the net force acting on the particle. the particle is displaced a distance A towards left from the equilibrium position E and released from rest at t=0.
Velocity-time graph of the particle is
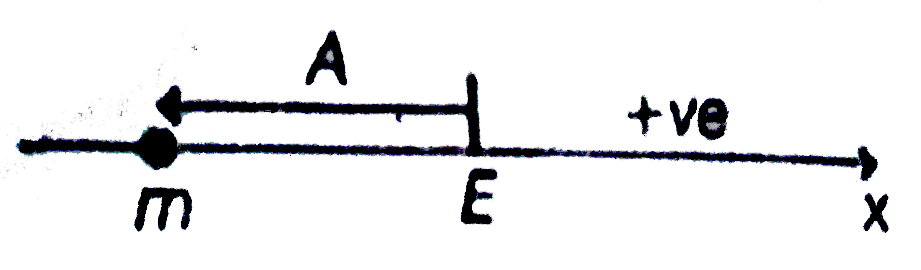
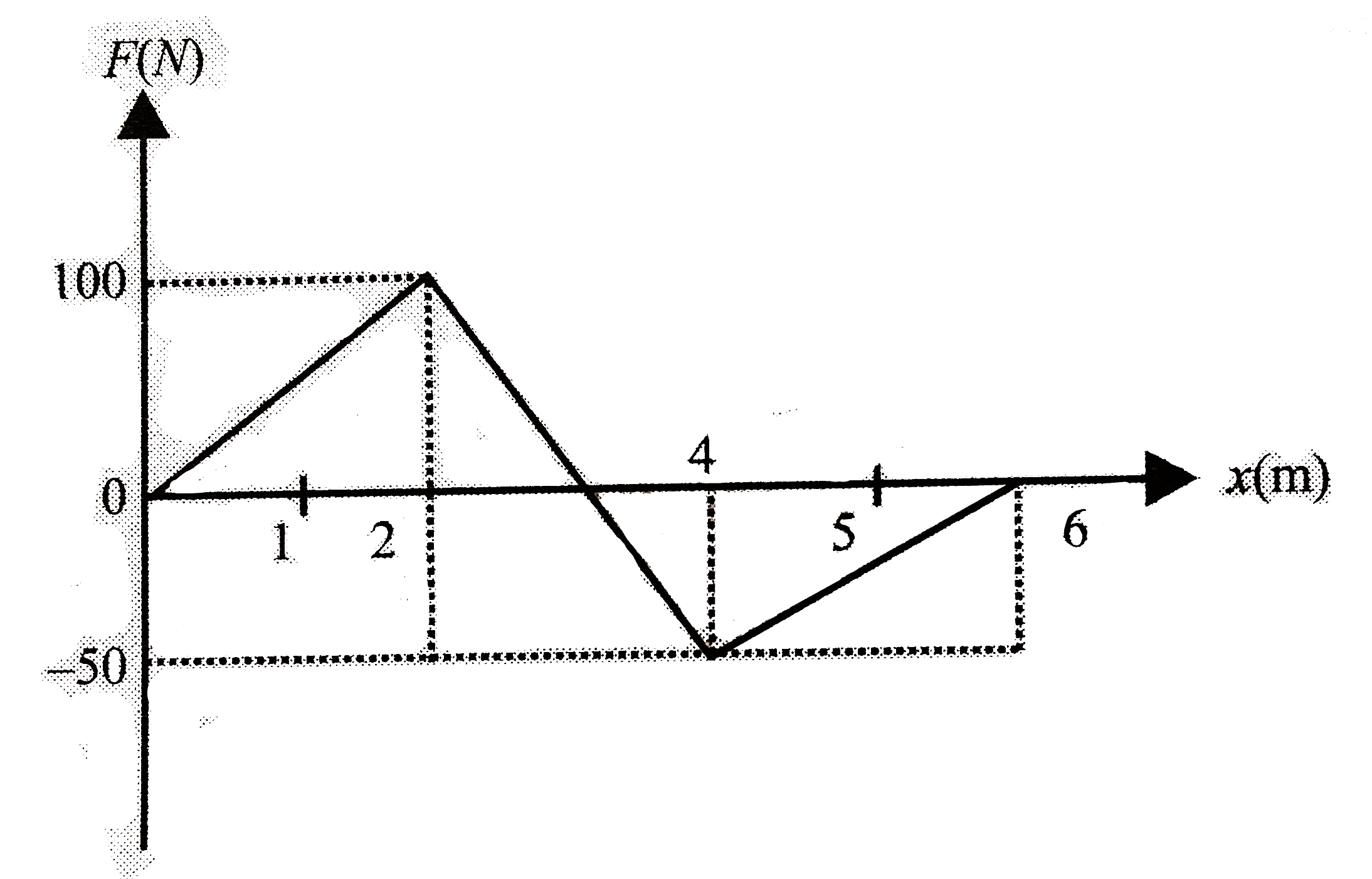
View SolutionA stationary particle of mass m=1.5kg is acted upon by a variable force. The variation of force with respect to displacement is plotted in figure.
a. Calculate the velocity acquired by the particle after getting displaced through 6m.
b. What is the maximum speed attained by the particle and at what time is it attained?
View SolutionA block of mass m at rest is acted upon by a force F for a time t. The kinetic energy of block after time t is
View SolutionA particle is acted upon by a force given by F=(12t−3t2)N, where is in seconds. Find the change in momenum of that particle from t=1 to t=3 sec.
View SolutionA particle of mass 2kg is moving in free space with velocity →v0=(2ˆi−3ˆj+ˆk)m/s is acted upon by force →F=(2ˆi+ˆj−2ˆk)N. Find velocity vector of the particle 3s after the force starts acting.
View SolutionA particle moving along the x axis is acted upon by a single force F = F0e−kx , where F0 and k are constants. The particle is released from rest at x = 0. It will attain a maximum kinetic energy of :
View Solution
