A particle of mass m initially at rest is acted upon by a unidirectional force F=F∘cos(π2t). The distance travelled by the particle when it stops first in the subsequent motion is ,
2F0mπ
4F0π2m
8F0mπ2
2F0π2m
The correct Answer is:C
dvdt=F0mcosπt2⇒∫v0dv=F0m∫t0cosπt2dt⇒v=2F0πmsinπt2
⇒Distance traveled from t= 0 to t = 2sec . =∫20vdt
= shaded area =(2F0)(πm)∫20sin(πt)2dt=8F0π2m
(##VMC_PHY_XI_WOR_BOK_01_C02_E03_031_S01.png" width="80%">
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE MAIN (archive)19videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)14videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 175videos
KINEMATICS OF A PARTICLE
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)1videos
JEE MAIN REVISON TEST-23
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
Similar Questions
A particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionVelocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
View SolutionA body of mass 500 g, initially at rest, is acted upon by a force which causes it to move a distance of 4 m in 2 s, Calculate the force applied.
View SolutionThe motion of a particle is described by the equation at u=at.The distance travelled by the particle in the first 4 seconds
View SolutionA particle initially at rest is subjected to two forces, one is constant, the other is retarding force proportional to the particle velocity. In the subsequent motion of the particle, the acceleration
View Solutionx−t equation of a particle in SHM is
x=(4cm)cos(π2t)
Here ,t is in seconds. Find the distance travelled by the particle in first three seconds.View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionA particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
View SolutionA particle moves in one dimension from rest under the influence of a force that varies with the distance travelled by the particle as shown in the figure. The kinetic energy of the particle after it has travelled 3m is:
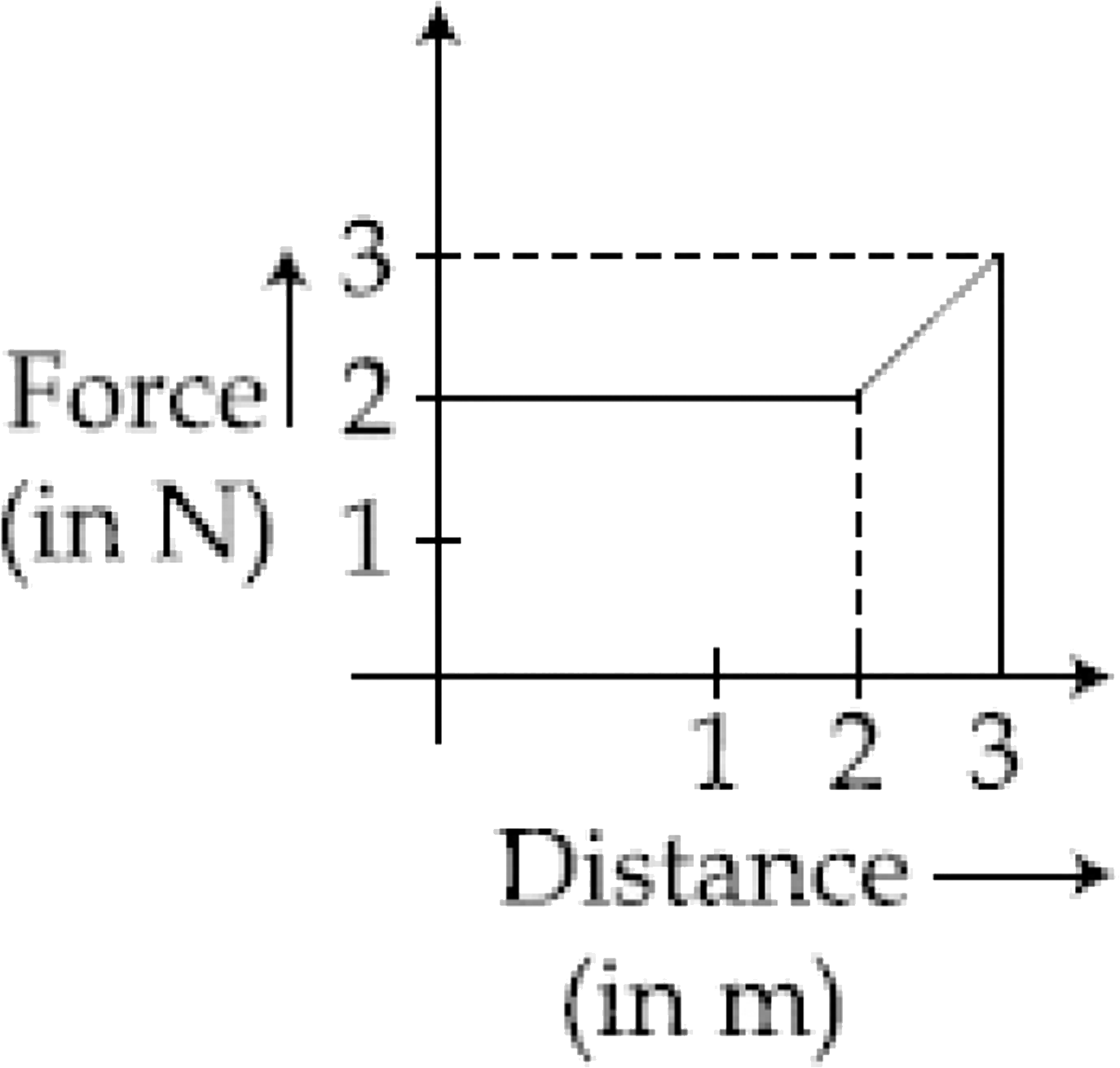 View Solution
View SolutionA particle of mass 2kg is initially at rest. A force starts acting on it in one direction whose magnitude changes with time. The force time graph is shown in figure. Find the velocity of the particle at the end of 10s.
 View Solution
View Solution

