Two sources of sound moving with same speed v and emitting frequency of 1400 Hz are moving such that one source s1 is moving towards the observer and s2 is moving away from observer. If observer hears beat frequency of 2 Hz. Then find the speed of source. Given vsound>>vsource and vsound=350ms
4
14
2
12
The correct Answer is:B
To solve the problem, we will use the concept of the Doppler effect for sound waves. The beat frequency is the difference between the frequencies heard from two sources moving towards and away from the observer.
1. Understanding the Problem:
- We have two sound sources, S1 moving towards the observer and S2 moving away from the observer.
- Both sources emit a frequency f0=1400Hz.
- The speed of sound in air, c=350m/s.
- The beat frequency heard by the observer is fb=2Hz.
2. Applying the Doppler Effect:
- For the source S1 moving towards the observer, the observed frequency f1 is given by:
f1=f0cc−v
- For the source S2 moving away from the observer, the observed frequency f2 is given by:
f2=f0cc+v
3. Finding the Beat Frequency:
- The beat frequency fb is the absolute difference between the two frequencies:
fb=|f1−f2|
- Substituting the expressions for f1 and f2:
fb=∣∣∣f0cc−v−f0cc+v∣∣∣
4. Simplifying the Expression:
- Factor out f0:
fb=f0∣∣∣cc−v−cc+v∣∣∣
- Combine the fractions:
fb=f0∣∣∣c(c+v)−c(c−v)(c−v)(c+v)∣∣∣
- Simplifying the numerator:
fb=f0∣∣∣cv+cv(c−v)(c+v)∣∣∣=f0∣∣∣2cv(c−v)(c+v)∣∣∣
5. Setting Up the Equation:
- We know fb=2Hz, so we set up the equation:
2=1400∣∣∣2⋅350⋅v(350−v)(350+v)∣∣∣
6. Solving for v:
- Rearranging gives:
2=1400⋅700v(350−v)(350+v)
- Simplifying further:
2=980000v(350−v)(350+v)
- Cross-multiplying:
2(350−v)(350+v)=980000v
- Expanding the left side:
2(122500−v2)=980000v
- This simplifies to:
245000−2v2=980000v
- Rearranging gives:
2v2+980000v−245000=0
7. Using the Quadratic Formula:
- We can use the quadratic formula v=−b±√b2−4ac2a where a=2, b=980000, and c=−245000.
- Calculate the discriminant:
b2−4ac=(980000)2−4⋅2⋅(−245000)
- Solve for v.
8. Final Calculation:
- After calculating the values, we find that:
v≈0.25m/s
Thus, the speed of the source is approximately 0.25 m/s.
- We have two sound sources, S1 moving towards the observer and S2 moving away from the observer.
- Both sources emit a frequency f0=1400Hz.
- The speed of sound in air, c=350m/s.
- The beat frequency heard by the observer is fb=2Hz.
- For the source S1 moving towards the observer, the observed frequency f1 is given by:
f1=f0cc−v
- For the source S2 moving away from the observer, the observed frequency f2 is given by:
f2=f0cc+v
- The beat frequency fb is the absolute difference between the two frequencies:
fb=|f1−f2|
- Substituting the expressions for f1 and f2:
fb=∣∣∣f0cc−v−f0cc+v∣∣∣
- Factor out f0:
fb=f0∣∣∣cc−v−cc+v∣∣∣
- Combine the fractions:
fb=f0∣∣∣c(c+v)−c(c−v)(c−v)(c+v)∣∣∣
- Simplifying the numerator:
fb=f0∣∣∣cv+cv(c−v)(c+v)∣∣∣=f0∣∣∣2cv(c−v)(c+v)∣∣∣
- We know fb=2Hz, so we set up the equation:
2=1400∣∣∣2⋅350⋅v(350−v)(350+v)∣∣∣
- Rearranging gives:
2=1400⋅700v(350−v)(350+v)
- Simplifying further:
2=980000v(350−v)(350+v)
- Cross-multiplying:
2(350−v)(350+v)=980000v
- Expanding the left side:
2(122500−v2)=980000v
- This simplifies to:
245000−2v2=980000v
- Rearranging gives:
2v2+980000v−245000=0
- We can use the quadratic formula v=−b±√b2−4ac2a where a=2, b=980000, and c=−245000.
- Calculate the discriminant:
b2−4ac=(980000)2−4⋅2⋅(−245000)
- Solve for v.
- After calculating the values, we find that:
v≈0.25m/s
Topper's Solved these Questions
Similar Questions
Knowledge Check
A sound source is moving towards a stationary observer with 1/10 of the speed of sound. The ratio of apparent to real frequency is
A109B(109)2C(1110)2D1110
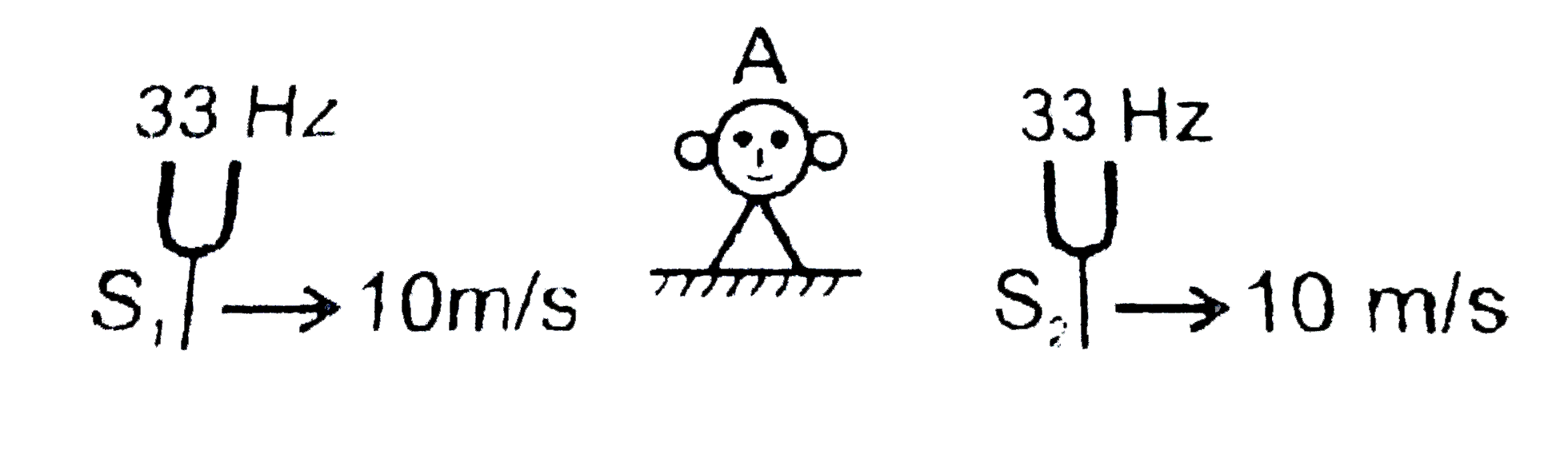
Observer A is at rest. Source S1 is moving towards observer A and source S2 is moving away from observer A. velocity of sound is 330msec. β= beat frequency heard per second by A. Approximate value of β is:
View SolutionA source of sound is travelling towards a stationary observer. The frequency of sound heard by the observer is 25% more that the actual frequency. If the speed of sound is v, that of the source is
View SolutionTwo tuning forks with natural frequencies of 340Hz each move relative to a stationary observer. One fork moves away form the observer, while the other moves towards him at the same speed. The observer hears beats of frequency 3Hz. Find the speed of the tuning fork.
View Solutionif the speed of a sound source is equal to the speed fo sound and the source is moving away from the observer, then the ratio of apparent frequency to the original frequency is
View SolutionA source of sound emitting a note of frequency 200 Hz moves towards an observer with a velocity v equal to the velocity of sound. If the observer also moves away from the source with the same velocity v, the apparent frequency heard by the observer is
View SolutionA source is moving towards an observer with a speed of 20 m / s and having frequency of 240 Hz . The observer is now moving towards the source with a speed of 20 m / s . Apparent frequency heard by observer, if velocity of sound is 340 m / s , is
View SolutionA sound source is moving with speed 50m/s towards a fixed observer. Frequency observed by observer is 1000Hz. Find out apparent frequency observed by observer when source is moving away from observer (Speed of sound =350m/s)
View Solution
