Solution set of 3x(3x–1)+2=|3x–1|+|3x–2| contains
singleton set
two elements
at least four elements
infinite elements
The correct Answer is:A
To solve the equation 3x(3x−1)+2=|3x−1|+|3x−2|, we will follow these steps:
Step 1: Substitute 3x with t
Let t=3x. The equation then becomes:
t(t−1)+2=|t−1|+|t−2|
Step 2: Analyze the absolute values
We need to consider different cases based on the value of t to handle the absolute values.
Case 1: t<1
In this case, both t−1 and t−2 are negative:
|t−1|=−(t−1)=−t+1
|t−2|=−(t−2)=−t+2
Substituting these into the equation gives:
t(t−1)+2=−t+1−t+2
This simplifies to:
t2−t+2=−2t+3
Rearranging gives:
t2+t−1=0
Step 3: Solve the quadratic equation
Using the quadratic formula t=−b±√b2−4ac2a:
t=−1±√12−4⋅1⋅(−1)2⋅1=−1±√52
Calculating the roots:
t1=−1+√52,t2=−1−√52
Since t must be positive (as t=3x), we only consider t1=−1+√52.
Step 4: Check if t1<1
We need to check if −1+√52<1:
−1+√5<2⟹√5<3 (True)
Thus, t1 is valid for this case.
Step 5: Case 2: 1≤t<2
Here, t−1 is non-negative and t−2 is negative:
|t−1|=t−1,|t−2|=−t+2
Substituting gives:
t(t−1)+2=(t−1)+(−t+2)
This simplifies to:
t2−t+2=1
Rearranging gives:
t2−t+1=0
The discriminant is:
(−1)2−4⋅1⋅1=1−4=−3 (No real roots)
Step 6: Case 3: t≥2
In this case, both t−1 and t−2 are non-negative:
|t−1|=t−1,|t−2|=t−2
Substituting gives:
t(t−1)+2=(t−1)+(t−2)
This simplifies to:
t2−t+2=2t−3
Rearranging gives:
t2−3t+5=0
The discriminant is:
(−3)2−4⋅1⋅5=9−20=−11 (No real roots)
Conclusion
The only solution comes from Case 1, which gives us a single valid solution:
t=−1+√52
Thus, the solution set of the original equation contains only one element.
Final Answer
The solution set of the equation is a singleton set.
Let t=3x. The equation then becomes:
t(t−1)+2=|t−1|+|t−2|
We need to consider different cases based on the value of t to handle the absolute values.
In this case, both t−1 and t−2 are negative:
|t−1|=−(t−1)=−t+1
|t−2|=−(t−2)=−t+2
Substituting these into the equation gives:
t(t−1)+2=−t+1−t+2
This simplifies to:
t2−t+2=−2t+3
Rearranging gives:
t2+t−1=0
Using the quadratic formula t=−b±√b2−4ac2a:
t=−1±√12−4⋅1⋅(−1)2⋅1=−1±√52
Calculating the roots:
t1=−1+√52,t2=−1−√52
Since t must be positive (as t=3x), we only consider t1=−1+√52.
We need to check if −1+√52<1:
−1+√5<2⟹√5<3 (True)
Thus, t1 is valid for this case.
Here, t−1 is non-negative and t−2 is negative:
|t−1|=t−1,|t−2|=−t+2
Substituting gives:
t(t−1)+2=(t−1)+(−t+2)
This simplifies to:
t2−t+2=1
Rearranging gives:
t2−t+1=0
The discriminant is:
(−1)2−4⋅1⋅1=1−4=−3 (No real roots)
In this case, both t−1 and t−2 are non-negative:
|t−1|=t−1,|t−2|=t−2
Substituting gives:
t(t−1)+2=(t−1)+(t−2)
This simplifies to:
t2−t+2=2t−3
Rearranging gives:
t2−3t+5=0
The discriminant is:
(−3)2−4⋅1⋅5=9−20=−11 (No real roots)
The only solution comes from Case 1, which gives us a single valid solution:
t=−1+√52
Thus, the solution set of the original equation contains only one element.
The solution set of the equation is a singleton set.
Similar Questions
Knowledge Check
The solution set of −3+x≤8x3+2≤143+2x,x∈R is
A−3<x<4B−3<x≤4C−3≤x≤4D−3≤x<4The solution set of −223<x+13≤313,x∈R is
A{x:−3<x<3,x∈R}B{x:−3≤x<3,x∈R}C{x:−3≤x≤3,x∈R}D{x:−3<x≤3,x∈R}The solution set of 2x+13<3x−25x∈R on the number line is
A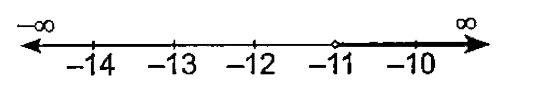 B
B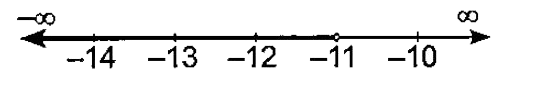 C
C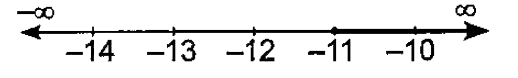 D
D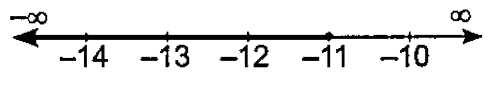
The solution set of (x+1x)2−32(x−1x) =4 when x≠0 is
View Solutionsolution set of the inequality √7−x > 2x-3 , is contained by the set
View SolutionThe solution set of the inequation |2x−3|<|x+2|, is
View SolutionThe solution set of (35)x=x−x2−9 is
View SolutionThe number of solutions of x1+x2+x3=51 (X1, X2, X3 being odd natural numbers) is
View Solution
