The solution set of is
{0}
{1}
none of these
The correct Answer is:C
To solve the equation (35)x=x−x2−9, we will analyze both sides of the equation by graphing and determining the points of intersection.
Step 1: Rewrite the equation
We start with the equation:
(35)x=x−x2−9
Step 2: Analyze the left-hand side
The left-hand side, (35)x, is an exponential function. Since 35<1, this function will be decreasing. As x approaches infinity, (35)x approaches 0, and as x approaches negative infinity, (35)x approaches infinity.
Step 3: Analyze the right-hand side
The right-hand side, x−x2−9, is a quadratic function. We can rewrite it as:
−x2+x−9
This is a downward-opening parabola (since the coefficient of x2 is negative).
Step 4: Find the vertex of the quadratic
The vertex of a quadratic ax2+bx+c is given by the formula x=−b2a. Here, a=−1 and b=1:
x=−12⋅−1=12
Now we can find the value of the quadratic at x=12:
y=−(12)2+12−9=−14+12−9=−14+24−364=−354
Step 5: Determine the y-intercept
To find the y-intercept of the quadratic, we set x=0:
y=0−0−9=−9
Step 6: Analyze the discriminant
To find the number of real roots of the quadratic x−x2−9, we calculate the discriminant D=b2−4ac:
D=12−4(−1)(−9)=1−36=−35
Since D<0, the quadratic does not intersect the x-axis, meaning it has no real roots.
Step 7: Conclusion
Since the left-hand side (35)x approaches 0 as x increases and the right-hand side x−x2−9 is always less than 0 (as shown by the vertex and y-intercept), there are no points of intersection between the two graphs. Therefore, the solution set is empty.
The final answer is:
Solution set: ∅
We start with the equation:
(35)x=x−x2−9
The left-hand side, (35)x, is an exponential function. Since 35<1, this function will be decreasing. As x approaches infinity, (35)x approaches 0, and as x approaches negative infinity, (35)x approaches infinity.
The right-hand side, x−x2−9, is a quadratic function. We can rewrite it as:
−x2+x−9
This is a downward-opening parabola (since the coefficient of x2 is negative).
The vertex of a quadratic ax2+bx+c is given by the formula x=−b2a. Here, a=−1 and b=1:
x=−12⋅−1=12
Now we can find the value of the quadratic at x=12:
y=−(12)2+12−9=−14+12−9=−14+24−364=−354
To find the y-intercept of the quadratic, we set x=0:
y=0−0−9=−9
To find the number of real roots of the quadratic x−x2−9, we calculate the discriminant D=b2−4ac:
D=12−4(−1)(−9)=1−36=−35
Since D<0, the quadratic does not intersect the x-axis, meaning it has no real roots.
Since the left-hand side (35)x approaches 0 as x increases and the right-hand side x−x2−9 is always less than 0 (as shown by the vertex and y-intercept), there are no points of intersection between the two graphs. Therefore, the solution set is empty.
Solution set: ∅
Similar Questions
Knowledge Check
The solution set of |x−1|x>2 is
A0<x<13Bx<13Cx>13D13<x<1The solution set of 2x+13<3x−25x∈R on the number line is
A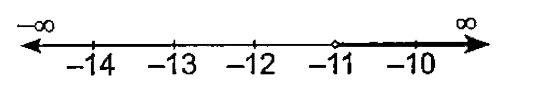 B
B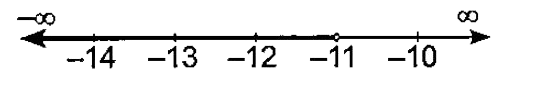 C
C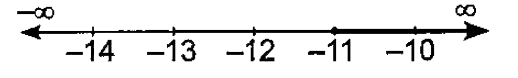 D
D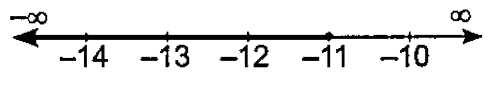
The solution set of −223<x+13≤313,x∈R is
A{x:−3<x<3,x∈R}B{x:−3≤x<3,x∈R}C{x:−3≤x≤3,x∈R}D{x:−3<x≤3,x∈R}
